Higher beings, these words are for you alone.
Your great strength marks you amongst us. 
Focus your soul and you shall achieve feats of which others can only dream.
-- Hallownest

4D skewb

In the rest of this series, I will focus on introducing my 4D skewb re-implementation and hopefully a successful solve to the puzzle. It will be a re-implementation because I cannot take the credit I don't deserve. MPUlt, the software that provides various high-dimensional puzzles, supports the configurations as my descriptions to hyperskewb yesterday. I wasn't aware of this when I began this series, but obviously I should have done more homework.

So, it won't be an original invention, but still serves as a good exercise and inspiration.

It will be a WebGL-based implementation. Also, I have to emphasize this: Thanks to Pastleo, whose Ironman series Introduction to WebGL is the template of this htperskewb project. I appreciate the author and his comprehensive articles very much.

Let's move on to 4D skewb.

What does it look like?

I will keep using the following visual representation based on the net of the hypercube, where

• orange cell is the x = -1 hyperplane
• red cell is the x = 1 hyperplane
• white cell is the y = -1 hyperplane
• yellow cell is the y = 1 hyperplane
• green cell is the z = -1 hyperplane
• blue cell is the z = 1 hyperplane
• pink cell is the w = -1 hyperplane
• coffee cell is the w = 1 hyperplane

as the figure shows,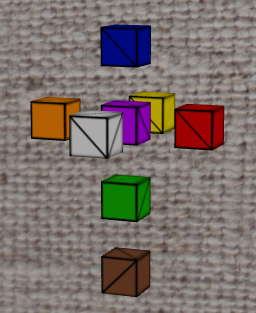

Basically, we can first grasp some sense from seeing how hyperplne x + y + z + w = 0 cuts a hyper cube. This will not result in a 4D skewb, because a 4D skewb requires 7 more hyperplane cuts. Yet, the visualization serves as a good entry for the reader to comprehensing a 4D skewb,

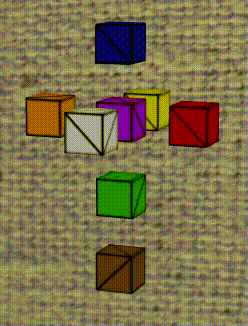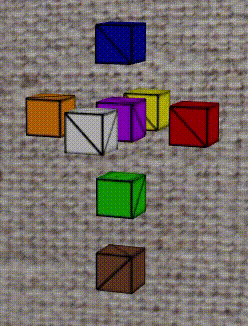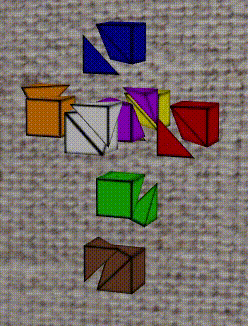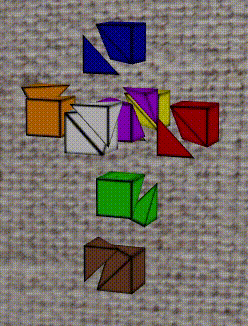
The easist one for the reader to comprehend would be the pink one. Since it is the w = -1 boundary by it self, the intersection with x + y + z + w = 0 is thus reduced to x + y + z = 1, which is straight forward. The cutting surface has three vertices (1, 1, -1), (1, -1, 1), (-1, 1, 1).

For other cells, they are not that straightforward. Let's take the red cell as an example. It is the x = 1 boundary fo the hypercube, so the cut should be y + z + w = -1. Although we are familir with the x-y-z 3D cartesian coordination system and its right-handness property, how should we interpret the red cube? I find it helpful to recall some 3D (2D net) analogy, but we can try directly think through it now.

The red and the pink shares a face, this is a fact before and after the folding of this net into the hypercube. This means, the y- and z-axis for the pink cell are of the same directions for the red cell. The seemingly x-axis of red cube is actually w-axis. The explanation to this is that, all cells other than pink (W-) and coffee (W+) are connected to the two cell. It means that the w-axis direction of those 6 cube are from the pink to the coffee. For the red cell, it is from the left-hand side to the right-hand side. The coffee cell seems to be only in the bottom of the whole net, but since it is a net of the hypercube, we can reasonably re-organize the position of any cubes. The coffee cube can legally go to the right-hand side of the red.

If this is too hard to comprehend, the reader is suggested to re-visit the net of a cube (skewb) in the past few days. Or any net of a cube would do. For each square in the net, they share the same x- and y-axis on a 2D plane, but we are talking about the axes when they fold.

With the above mindset, The reader can now examine if my animation of the x + y + z + w = 0 cut is correct for all the cubes. The most challenging one is the coffee cell. While the equation defines the cutting hyperplane, its two inequlities defines the two part of the deep-cut puzzle. The proof to above claims are left as excercises to the reader, but here I provide the x + y + z + w < 0 part, as follows

Cutting cell

For a 2D observer, they can compute the cut on each face based on the net of a 3D cube, concluding that all the 6 segements form a regular hexagon. Just as skewb has multiple cutting surfaces, we are now aware of the fact that each cutting hyperplane generates a regular triangle per boundary cell. Therefore, the cutting cell, which is an intersection of the hypercube and the cuttinghyper plane x + y + z + w = 0, has 8 regular triangles as its boundary.

8 triangles. Does it mean that the cutting cell is a regular octahedron? I believe there was some mathematicians have already work out how to figure out the proofs and the theories, but I don't know how to generalize the concept to 5D and beyond yet. For 4D, it is simple to apply bruteforce method though, because there is only 6 vertices in this ocetahedron, whether it is a regular one or not. I won't provide details here. Instead, I will give the readers a simple hint and the visual representation of the octahedron.

The hint about the bruteforce method is, one can calculate all the vertex-to-vertex distance, and make them a matrix. As a regular octahedron, for any single vertex A, there are four vertices in unit distance, and the 6th vertex in 3^(1/2) unit distance. One can also normalize the axes according to the six vertices, and see why it is indeed a regular octahedron.

A short clip for reference is as follows,

For those who are interested in how I made these animation, they can check this repo. But I have to admit that, the way I doing these clips is not scalable for any 4D puzzles. They requires manuall calculations. It is lame, but in this series I need a quick and dirty way to craft 4D skewb, so it is what it is.

Conclusion

Today I show you many animation clips about the 4D skewb. I didn't spend much time writing the articles because they are just plain text to me, after I first came up with the hyperskewb ideas since mid August. It is much harder and needs much more work on the calculations for making the clips, because I don't know how to use any of the available 3D modeling software (yet?), so all the coordinates have to be calculated manually. Hopefully I have conveyed my ideas on 4D skewb and some geometry that makes sense to you.

小結

展示 4D skewb 的靜態性質。