今天要來討論的是樹的尋訪，「尋訪」或是「遍歷」的意思就是把所有樹的節點都看過的意思啦！不曉得大家還記不記得之前學過的樹，如果忘記了可以再往前看呦。

想想看一個比較簡單的Case，假如今天我們的樹是長這樣，我有幾種把樹節點都尋訪完的排列方式呢？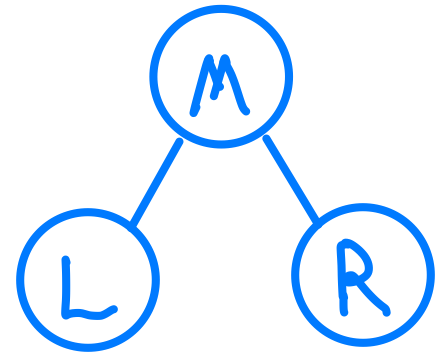

答案是3！= 6種，也就是LMR、MLR、LRM、RML、MRL、RLM。

這邊我們可以發現，其實最最最主要就是「左右節點」跟我們「父子節點」的關係，共有三種狀態，分別是先尋訪父節點然後再尋訪左右節點，還有先尋訪左右節點在尋訪父節點，以及在左右子樹中間穿插尋訪父節點。
順帶一題在尋訪的時候，我們都會習慣先尋訪完左子樹在尋訪右子樹，所以剛剛上面說到的6種狀況，我們可以先簡化成3種，也就是只有LMR、MLR、LRM，可以發現這三種情況，左節點始終排在右節點前面(其實另外3種也就只是把左節點跟右節點對調而已)。

依照這三種尋訪的方式我們通常稱LMR為InOrder Traversal、MLR為Preorder Traversal、LRM為PostOrder Traversal，至於要怎麼記呢，其實很簡單~我們以父節點為主
父節點在前面的就是Preorder Traversal，英文的「Pre」就有在前面的意思嘛~

那父節點在後面的，就是PostOrder Traversal，「Post」也就是在後面的意思。

那父節點在中間的我們會發現，當我們依照LMR的順序尋訪完一個Binary Search Tree那他的值就會從小到大排序過的樣子，所以我們就叫他InOrder。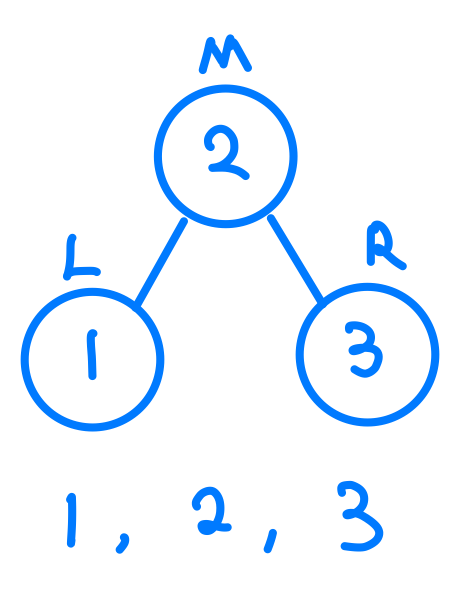

樹的結構哪有那麼簡單

沒錯，真正的樹不會只有這樣傻傻的3個節點，真正的樹複雜多了，那我們應該怎麼去尋訪更複雜更大的樹狀結構呢？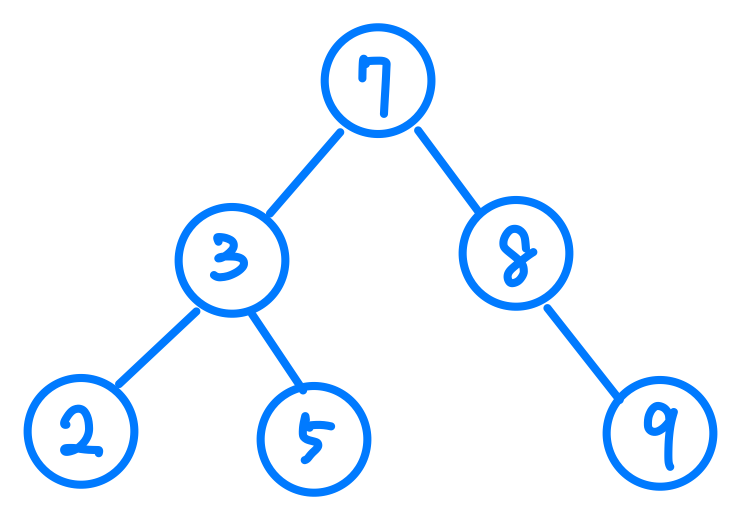

我們以InOrder為例。
首先，我們先把焦點放在「7」這個節點上，剛剛說過，InOrder的順序是左中右，所以依照我這個「7
」節點為中間的節點，我們先不用管他左邊跟右邊到底有多少個節點，我們把它想像成這樣。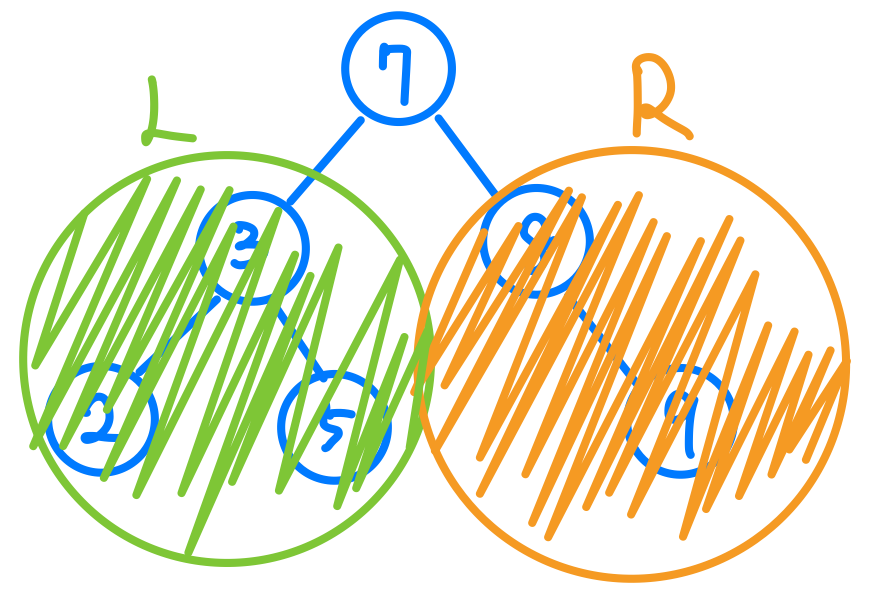

依照LMR的尋訪路線，現在問題變成先尋訪完左邊那一群後換到「7」，接著尋訪右邊那一群，對吧！所以現在問題就變成如何尋訪左邊那一群了，我們現在先把焦點移到「3」這個節點上去做InOrder Traversal，我們會發現其實問題只需要關注「3」節點的左邊那一群及右邊那一群，於是我們先從左邊那一群開始尋訪發現到只有一個節點，右邊那一群也是只有一個節點，所以我可以在焦點為「3」節點裡，做完Traversal。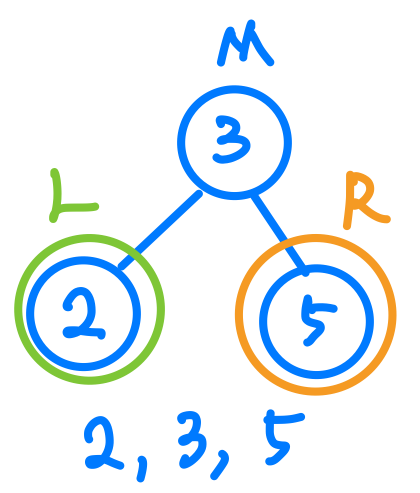

接下來再把焦點回到「7」這個節點，我們會發現我們已經完成了左邊的尋訪所以LMR的L已經完成了，接下來，我尋訪我自己，然後要往右邊尋訪，所以我的焦點此刻會變成「8」節點，接著我們在「8」節點一樣來做Tree Traversal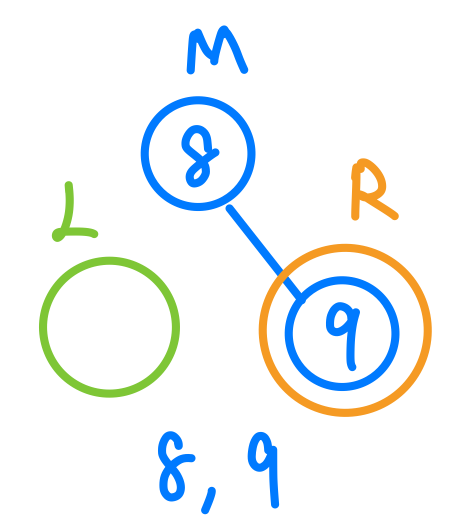

完成後我們發現不知不覺中就完成了整棵樹的尋訪，結果為2,3,5,7,8,9。

雖然步驟一步一步感覺很複雜，但是其實我們在做的不就是這樣嗎？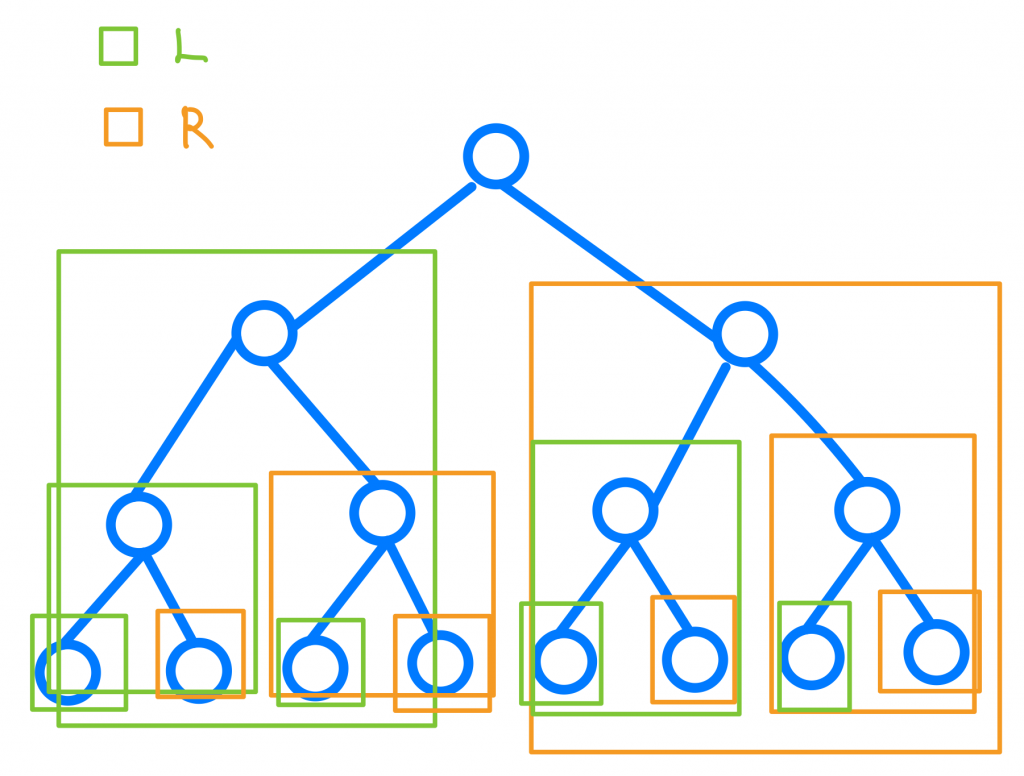

不管從哪個節點當焦點看下來，我都是在那個節點去做LMR的尋訪。

有沒有發現這個很像甚麼？沒有錯！遞迴。
樹的尋訪實際上就是遞迴非常經典的例子，我們當然也可以用迴圈來做，但是會相對來說困難一點，用遞迴的話就會簡單很多，因為樹的尋訪本身的思想就是一種遞迴思想，另外PostOrder跟PreOrder各位讀者也可以試著用這種方式來自己畫看看來加深印象喔！。

結論

今天我們介紹了樹的尋訪，從最簡單的3個節點的數到比較複雜的樹，其實觀念上都是差不多的，記得關鍵都是把左右子樹看待成子樹群，然後遞迴的去尋訪，當遇到Base Case也就是只有一個子樹，或是沒有子樹時，就代表完成了那個狀態下的尋訪囉。