早安大家,昨天講解了詞性標註在NLP領域的重要性跟怎麼實作之後,今天要介紹詞性標註背後的隱藏式馬可夫模型(HMM)到底是運用什麼原理在運算。應該會是這個系列文章到現在為止最複雜的也跟數學最靠近的一篇,但是我準備了一個自認滿有趣的設定來介紹它,所以請深呼吸一口氣然後抱著看戲(?)的心情來觀賞XDD
想了解HMM是什麼就必須先了解它的基礎,Markov Chain(馬可夫鏈)。所謂的馬可夫指的是一連串互相關聯的事件所形成得連鎖反應鏈。他可以用來計算在不同時間點變成不同狀態的可能性。為了理解上容易一點,這邊先不用語言舉例。假設小明每天就喜歡到不同的便利商店吃午餐,這些便利商店分別是7-11、全家跟萊爾富。如果小明欠錢不還,身為債主的我們想知道他在某個時間點會到哪間便利商店吃午餐,就可以把7-11、全家跟萊爾富當成三個不同的狀態,再透過小明去這些便利商店先後順序的機率計算我們想抓他的時間點他在哪間便利商店的機率比較高。我們可以把這個東西畫成像下圖這樣。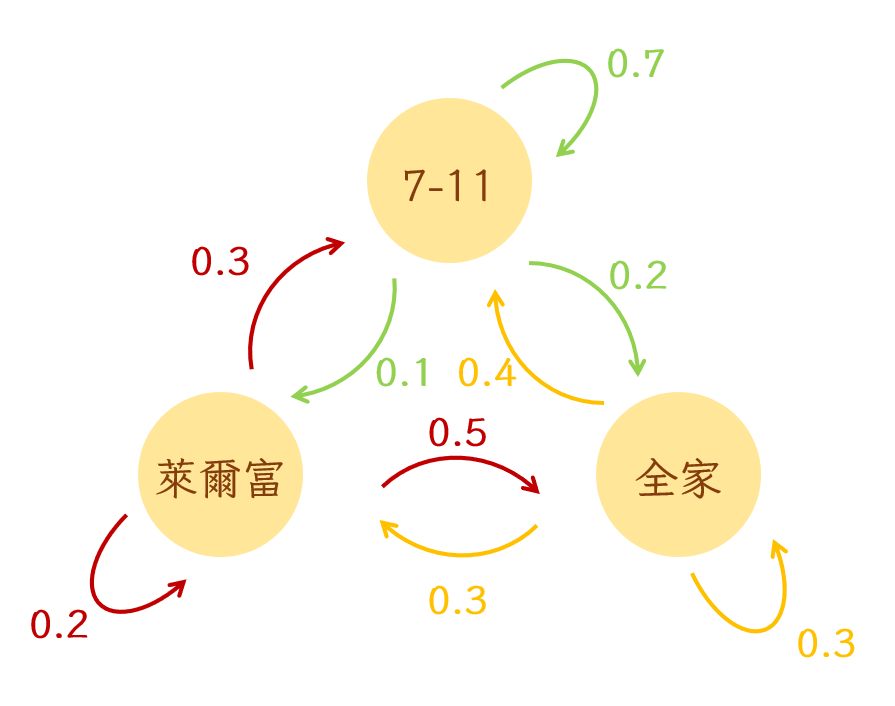
如果小明今天中午在7-11吃午餐,那他明天繼續吃7-11、換成吃萊爾富、跟換成吃全家的機率分別是0.7, 0.1, 0.2。因為在馬可夫模型的假設底下,被畫出來的狀態(便利商店)就是所有的可能性(所有小明午餐會去的地方),所以從一個狀態(state)畫出來的所有箭頭(機率)加起來會等於1。在使用馬可夫模型的時候,我們需要特別注意的另外一件事是,它假設每一個狀態的發生只會被前一個狀態影響。也就是說,小明今天選擇吃哪一間便利商店的原因只跟他昨天吃了什麼有關,並不會受到前天或大前天的影響。
到這個地方大家如果都還理解的話,我們就要開始計畫怎麼抓小明(進到計算的部分)了。假設今天小明到7-11、全家跟萊爾富的機率分別是0.5、0.4、0.1,那他明天到這三家便利商店的機率分別是多少呢?我們可以先把上面的圖轉換成下面這個表格以後再一個一個計算。舉例來說,明天去7-11的機率是:「今天去7-11的機率×明天去7-11的機率」加上「今天去全家的機率×明天去7-11的機率」再加上「今天去萊爾富的機率×明天去7-11」的機率。依此類推,我們可以計算出明天小明去這三家便利商店的機率就像下面這張圖一樣。
| 7-11(今)| 全家(今)| 萊爾富(今)
----- | --------- | ----------
7-11(明)| 0.7 | 0.4 | 0.3
全家(明)| 0.2 | 0.3 | 0.5
萊爾富(明)| 0.1 | 0.3 | 0.2

然後神奇的事情就發生了~原來這就是把他們變成矩陣相乘之後的結果啊!
依此類推,如果我們想知道後天小明去這三家便利商店的機率,只要把第二天的結果再乘上轉換機率的矩陣就行。也就是說,任何時候我們只要擁有前一個時間點狀態的機率跟轉換機率,我們就一定可以得知當下狀態的機率。這就是最簡單的馬可夫鏈模型。
既然都說了是最簡單的馬可夫鏈模型,當然就會有複雜一點的。接下來就繼續用小明舉例。如果小明出門主要有三種方法:走路、騎機車跟開車,去這三家便利商店的時候就各會有用這三種方式去的不同機率。因此我們可以再延伸出下面這個馬可夫鏈。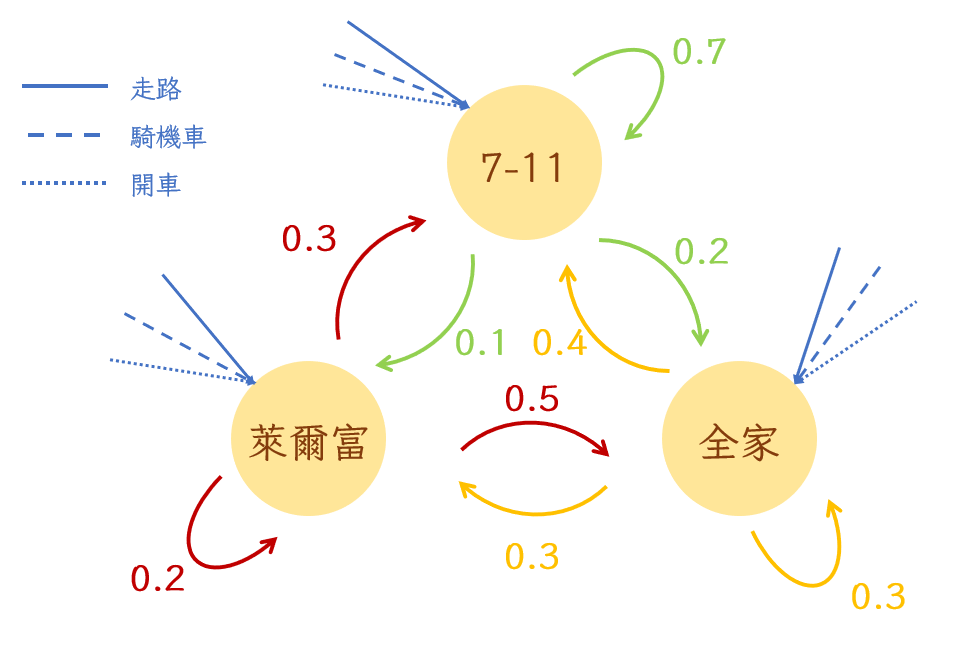
所謂的隱藏式馬可夫模型指的是狀態被隱藏的馬可夫鏈模型,以上面的例子來講就是我們不知道小明今天去了哪家便利商店,但是請徵信社潛伏在他家門口得到的觀察是他前天騎機車出門,昨天走路出門。如果是這樣的話,我們已經知道他前天跟昨天去的便利商店總共有3×3=9個可能性;知道他用不同方式去不同便利商店的機率;也知道他這兩天都是怎麼出門吃午餐的了,是不是就可以計算看看這九種可能性發生的機率了呢?當然可以。
| 走路| 騎機車| 開車
----- | --------- | ----------
7-11| 0.4 | 0.4 | 0.2
全家| 0.8 | 0.1 | 0.1
萊爾富| 0.2 | 0.3 | 0.5
現在我們一樣假設前天小明到7-11、全家跟萊爾富的機率分別是0.5、0.4、0.1,那麼第一天騎機車去7-11的機率就會是0.5×0.4=0.2,而第二天也走路去7-11的機率就是0.2×0.7×0.4=0.056,也就是說了明連續兩天去7-11的機率是0.056。按照這個方式算下去,我們就能得出這九種路徑分別發生的機率。再透過把第二天相同店家的路徑機率相加得到他昨天去各家便利商店的機率。接著就可以繼續計算他今天去這三家便利商店的機率了。如果再讓徵信社的人幫我們確認他今天怎麼出門,絕對能夠提高堵到他然後逼他還錢的機率。
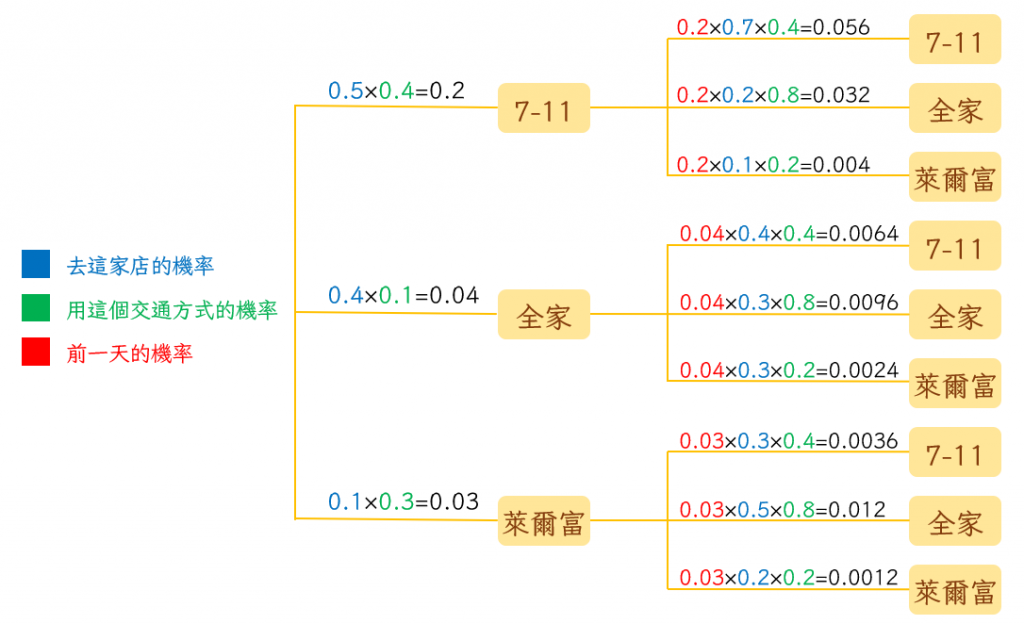
這樣大家應該理解HMM是怎麼運作的,我們終於可以回到正題-詞性標註。因為不同詞性之間一起出現的機率都不相同,我們可以把每一個詞的詞性想像成是上面例子裡面的便利商店。接下來因為同一個詞本身就可能是不同詞性,所以他自己是不同詞性的機率也不相同,我們可以把這個部分代換成上面例子裡的交通方式。現在你可能想問,但是這裡面詞性未知的話,兩邊不是都沒有答案嗎,我們要怎麼計算呢?
一般來說,詞性標註的工具都是經由大量資料訓練而來的。就像我們之前提到機器學習會用到人工標註的方法幫每一筆資料增加標籤一樣,用來訓練詞性標註模型的資料也事先經由語言學家標註過。透過這些資料組成的data base,我們就有了每個詞彙是不同詞性機率的依據,也拿到了不同詞性之間互相結合的機率。接下來只要在我們拿到一個句子之後,像剛剛一樣計算每一種路徑的可能性再找出最高的那個就可以了。至於NLP工程師用這些資料訓練模型的複雜計算我們就不多提了(如果有興趣的話可以參考這裡)。最後如果大家想進一部更仔細地看詞性標註HMM計算的過程,可以參考這篇文章,因為寫得太好了,我自覺沒有什麼可以說得更簡潔或更好的地方。如果上面的原理你都了解了的話,直接點進去看應該就可以掌握用HMM做詞性標註的奧秘了。
這篇真的是打到我頭昏眼花,花了一整個晚上才解決,所以如果你看懂了就表示我的努力沒有白費,當然如果你沒看懂絕對是我的問題,所以請多多在下面提問(或者鞭我也行)~明天見!
