昨天實作了Triangular mf，今天會使用GeneralizedBell mf，雖然我不常使用他，不過他的設定也蠻簡單的，先來看看他的特性吧。

特性

正如第25天介紹的，此隸屬函數有點像高斯函數跟梯形函數的合體，函數左右的值都快速地變小，但函數上方卻是比較平坦的。函數方程式為：

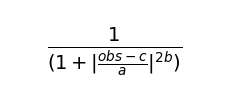
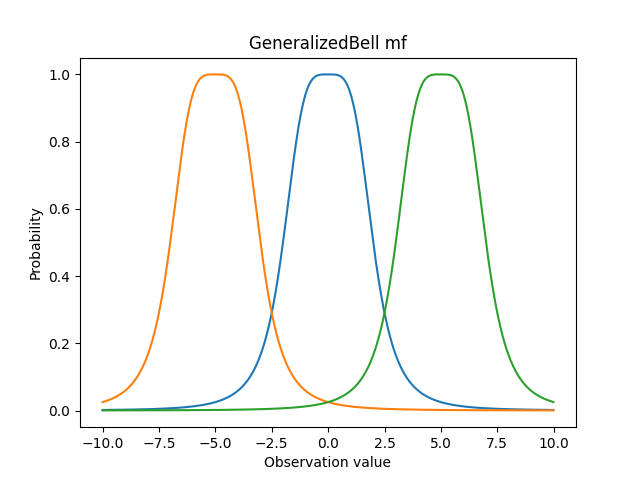
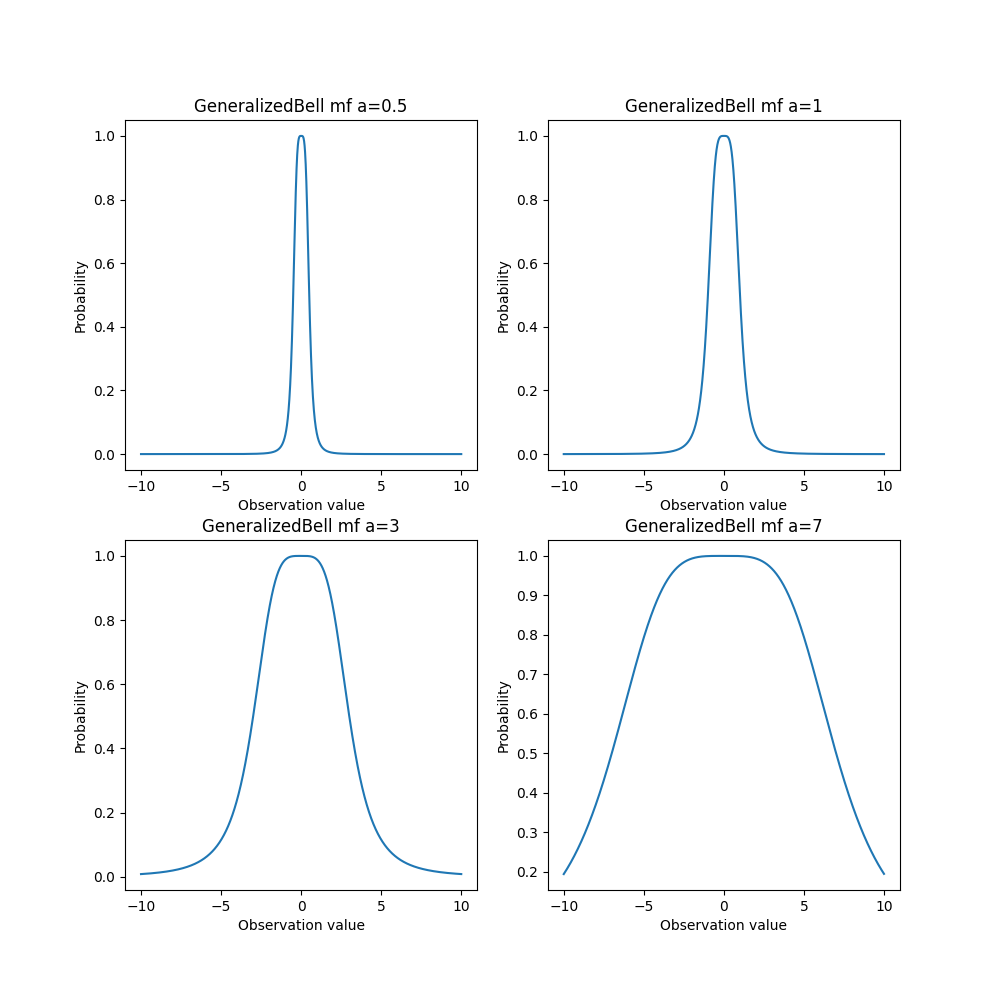
a為控制函數的寬度，正負不會影響，a越大函數越寬。

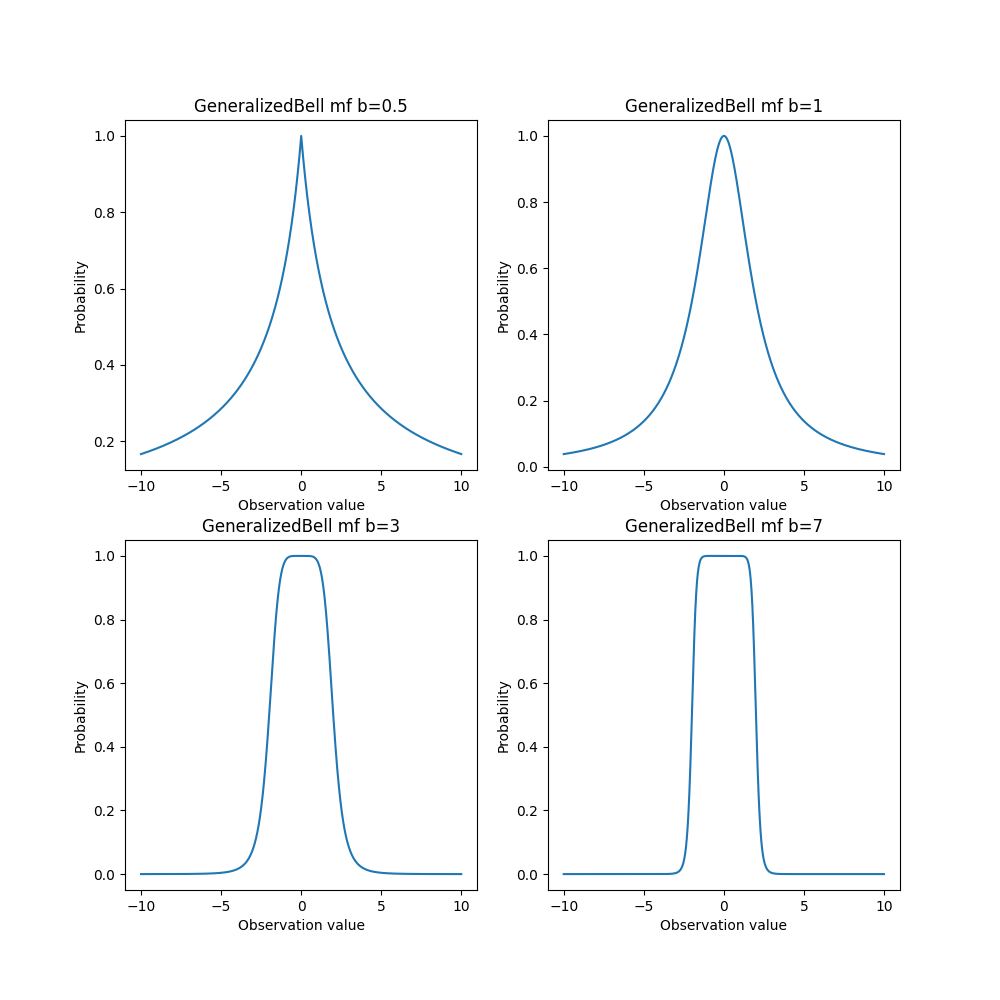
b為控制上面函數的平坦程度，需要大於0，b越小上面會越尖，反之上面越平坦。下圖可看到不同b值造成的影響。

c為控制函數水平平移的程度。

隸屬函數

需要注意的細節講完了，我們就來實際建立隸屬函數吧！

def GeneralizedBell_mf(self, obs, min_obs, max_obs):
        fuzzy_obs = np.zeros(shape=(7, 3))
        for i in range(len(obs)):
            l = [min_obs[i], max_obs[i]]
            u = sum(l) / 2  # 中點
            c = (l[0] - l[1]) / 3

            n = 1 / (1 + abs((obs - u - c) / 2) ** 4)
            m = 1 / (1 + abs((obs - u) / 2) ** 4)
            p = 1 / (1 + abs((obs - u + c) / 2) ** 4)
            fuzzy_obs[i][0] = n
            fuzzy_obs[i][1] = m
            fuzzy_obs[i][2] = p
        return fuzzy_obs.flatten()

更改觀察值也很簡單，昨天已經將需要更動的部分都更動好了，今天只需要改get_obs()中的輸出就行了！

把obs = self.triangular_mf(obs=obs, min_obs=self.min_obs, max_obs=self.max_obs)改成obs = self.generalizedBell_mf(obs=obs,min_obs=self.min_obs,max_obs=self.max_obs)即可，是不是非常容易呢？通常寫程式為了要方便修改所以在設計副程式通常都會考量到一致性。這些事前規劃好的話之後要修改就很方便。

接下來就訓練看看效果吧~

結語

今天帶各位實作了generalizedBell mf，基本上這些設定說難好像也沒那麼難，只需要把方程式用程式寫出來就好了，剩餘的細節再自己根據情況調整就好了。明天會帶大家實作Gaussian mf，這個我最常用的隸屬函數，基本上隸屬函數種類很多，但實作過之後遇到其他隸屬函數相信各位也都能輕鬆應付。那各位就明天見啦！