昨天使用過了GeneralizedBell_mf，今天帶大家實作我私心最常用的Gaussian&Sigmoid mf，這個函數沒有像前天Triangular mf那樣那麼好理解，不過實作卻相當簡單，因為不用分段，只需要宣告好高斯函數(常態分布)跟兩條sigmoid函數就好，聽起來很簡單，那就趁此機會趕快動手實作吧！go go！！

隸屬函數

如果忘記這兩個函數的話可以看看我第25天的文章，裡面有提到高斯函數(常態分布)跟sigmoid函數的數學方程式，跟Triangular mf還有GeneralizedBell_mf一樣，我們也是將觀察值陣列跟觀察值最大最小值陣列當作輸入，如果有要調整曲線或者傾斜程度等參數也可以將這些當作副程式的可變參數，為了方便我已經先設定好了。

我們先來複習一下常態分布曲線的數學公式長這樣：

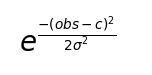
sigmoid的數學公式長這樣：

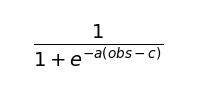
有了這些公式以後就可以來寫隸屬函數了，這邊我分別設定了：

σ(sigma)為觀察值最大值最小值的標準差除以4

b：觀察值最大值最小值的中點，基本上三條方程式都要平移到中點，然後sigmoid再沿x軸平移距離c。

c：到終點後分別要再沿x軸平移多少，sigmoid會使用到的。

def gaussian_mf(self, obs, min_obs, max_obs):
        fuzzy_obs = np.zeros(shape=(7, 3))
        for i in range(len(obs)):
            l = [min_obs[i], max_obs[i]]
            sigma = np.std(l) / 4  # 常態分布曲線的寬
            b = sum(l) / 2  # 中點
            c = (l[0] - l[1]) / 5  # sigmoid放在距離中點±1/5比例處

            n = 1 - (1 / (1 + np.e ** ((obs[i] - b - c))))
            m = np.e ** (-(obs[i] - b) ** 2 / (2 * sigma ** 2))
            p = (1 / (1 + np.e ** ((obs[i] - b + c))))
            fuzzy_obs[i][0] = n
            fuzzy_obs[i][1] = m
            fuzzy_obs[i][2] = p
        return fuzzy_obs.flatten()

更改觀察值也很簡單，跟昨天一樣，只需要改get_obs()中的輸出就行囉！

把obs = self.generalizedBell_mf(obs=obs, min_obs=self.min_obs, max_obs=self.max_obs)改成obs = self.gaussian_mf(obs=obs,min_obs=self.min_obs,max_obs=self.max_obs)即可。改完後就直接訓練看看吧。

建立隸屬函數心法、經驗

這邊統整一下我在建立隸屬函數的經驗！不知道前兩天建立時各位有沒有發現這些習慣。

1.我在建立隸屬函數的時候都習慣先建立一個全0陣列，形狀為(原本觀察值數量，隸屬函數中方程的數量)。

2.設定隸屬函數的定義域(觀察值最小值到最大值)

3.接下來會設定方程式變量，例如平移量，控制傾斜程度，寬度等等的變量。

4.定義隸屬函數中的方程式。

5.將值填入全0陣列。

6.最後展平成一維陣列。

拿gaussian mf舉例：

def gaussian_mf(self, obs, min_obs, max_obs):
        fuzzy_obs = np.zeros(shape=(7, 3))#建立一個全0陣列
        for i in range(len(obs)):
            l = [min_obs[i], max_obs[i]]#設定隸屬函數的定義域
						#設定方程式變量
            sigma = np.std(l) / 4
            b = sum(l) / 2
            c = (l[0] - l[1]) / 5
						#定義隸屬函數中的方程式
            n = 1 - (1 / (1 + np.e ** ((obs[i] - b - c))))
            m = np.e ** (-(obs[i] - b) ** 2 / (2 * sigma ** 2))
            p = (1 / (1 + np.e ** ((obs[i] - b + c))))
						#將值填入全0陣列
            fuzzy_obs[i][0] = n
            fuzzy_obs[i][1] = m
            fuzzy_obs[i][2] = p
        return fuzzy_obs.flatten()#展平成一維陣列

結語

今天帶大家使用了Gaussian mf，那模糊控制的部分也到此告一段落了，雖然我介紹的模糊控制只是冰山一角而已，不過正如我第一天所說的，我希望這些東西能夠符合高中生的程度，所以不打算講得太複雜，若有興趣的話可以搜尋fuzzy control，有非常多資源可以供給你深入了解喔！那關於我這一年在強化學習領域中學到的就差不多是這些了。這一年我是從0開始學起的，剛接觸時壓力真的很大，看不完的數學跟程式，所以想寫寫這個系列希望大家可以簡單的上手，再根據個人所需去學得更深，更廣。