前言

接下來要進入的章節是 m-way Search Tree，目的是為了鋪墊未來要教學的B tree of order m，本章節會先解釋為甚麼我們需要這個資料結構，再談一些數學特性，進入正題！

為甚麼需要 m-way search tree？

當資料量太大，大到沒辦法將資料一次性放到 memory 去操作，因此我們選擇令一個方法，將資料放在 Disk 中，分批載入 Memory，我們稱這樣的作法叫作 External search
然而，要將放在 DISK 中的資料載入到 Memory 時，要進行 I/O，會導致速度急遽下降，而製作成 m-way 的目的就是為了降低樹高（透過提高 Degree 數），藉此降低各 Level 載入記憶體的次數

最多 node 數、最多 key 總數、最小樹高

依 m-way Search Tree，令高度為 h

最多 Node 數

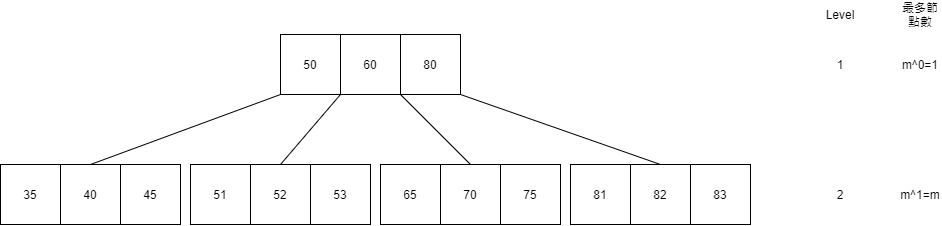
看到上圖，我們可以看成最多 node 數為

最多 Key 數

根據我們上面的式子，我們把最多的 node 數去乘上每個 node 所能乘載最多的 keys 數

即可得到最多的 keys 數

最小樹高

若給予固定量 n 的資料，節點內容納最多 keys 量，就可以形成最小樹高
因此可以想成
即可得到最小的樹高