樹的題目我個人認為也相對簡單的，而且非常非常適合用來練習遞迴思想，有以下的技巧讓大家參考看看。

樹的題目大概7成以上都是用遞迴去思考，要思考的點通常有兩個，分別是

• 我的Base Ca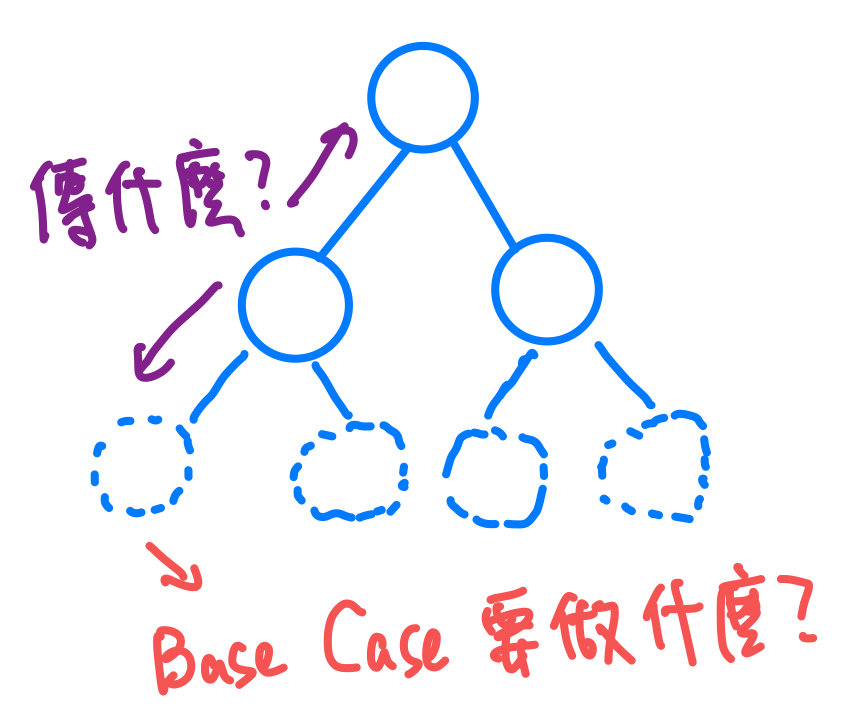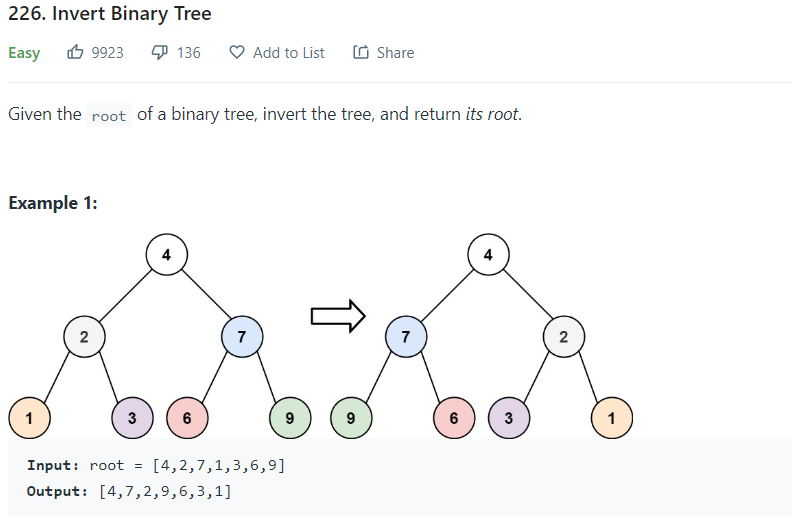se要做甚麼？
• 要決定傳甚麼值給父節點或子節點？
• 需不需要在遞迴時傳一些額外的狀態？
  
  只要掌握這三個，就輕鬆可以解決許多遞迴的問題囉。

範例1-Invert Binary Tree

我們先來看第一題。

我通常遇到樹的題目的時候，我會先畫一個三個節點的樹，然後先大概有個概念知道要做甚麼，然後在看這個操作能不能適用在不同層的節點上，以這個例子來說，我要做的是把左右節點交換。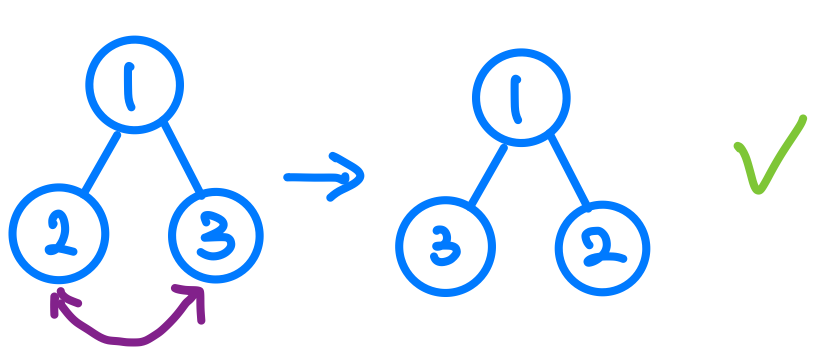

然後我們再用遞迴的做法去看是不是也適用在他的子節點，這邊可以發現，子節點也很適用喔！最後在記得加上Base Case就完成了。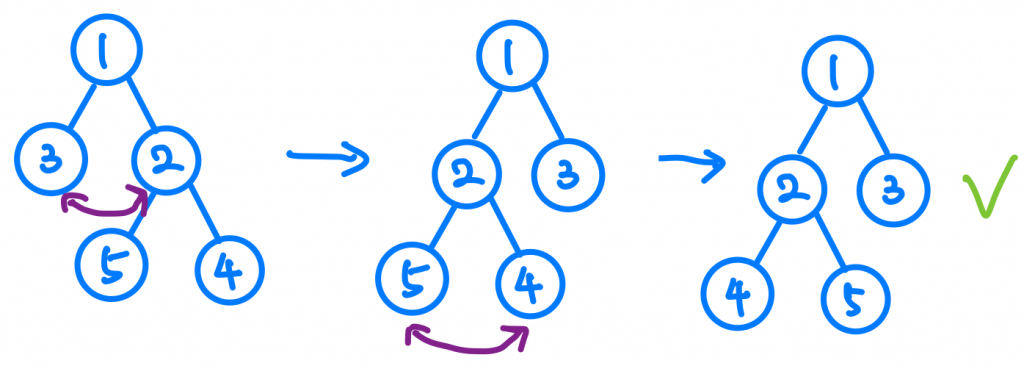

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        
        if root is None: return
        
        root.left, root.right = root.right, root.left
        
        self.invertTree(root.left)
        self.invertTree(root.right)
        
        return root

範例2-Validate Binary Search Tree

再我們來看這一題

一樣先畫三個節點的情況來看，我們第一個想會想說，我的右子節點是不是比我現在這個節點還要大？相反的左子節點要比我還要小，所以我們把現在節點值傳到下一個節點去比較就可以了。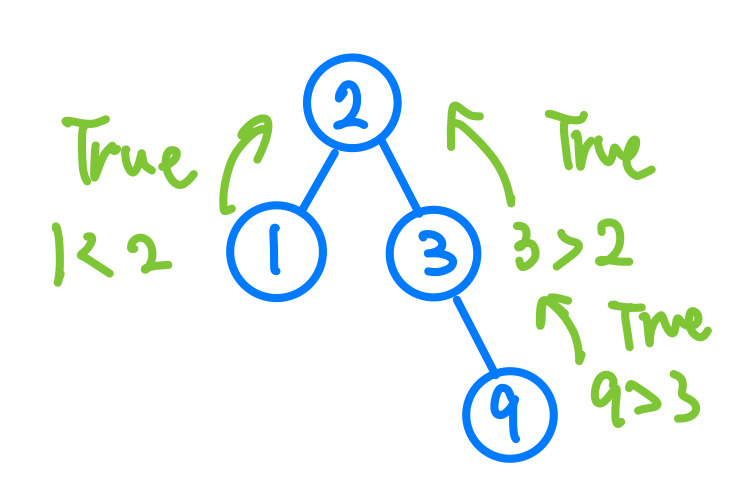

那是不是也是用在其他子節點呢？這邊我們仔細想想後會發現，如果是這種情況呢？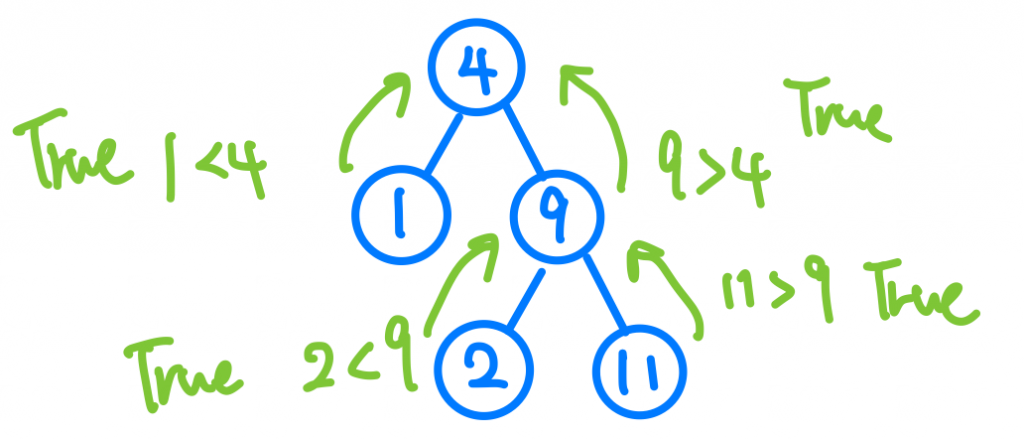

如果是這種情況，我們原本的想法結果會是True，但是正確答案應該要是False，因為在我的右邊節點群中，有一個節點數字比我還要小。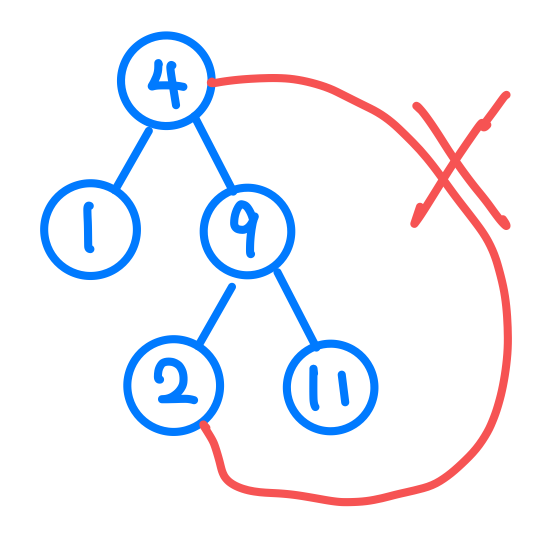

那我們希望的是甚麼？我們希望右邊的子節點群都會大於我現在的節點值對吧，這時候，我們可以在遞迴的參數裡，加一個約束的值，一開始是負無限大到無限大，如果我往左邊走，就更新我的無限大的值為我的現在節點值，如果我往右邊走，就更新我的無限小的值，為我的現在節點值，如果不在這個區間，那就可以return False，所以我的遞迴函式的參數會變成這樣(node, minimum, maximum)。那當我都沒有return False也就代表，可以return True了，所以我們的Base Case就可以Return True。看一下圖應該會好理解很多。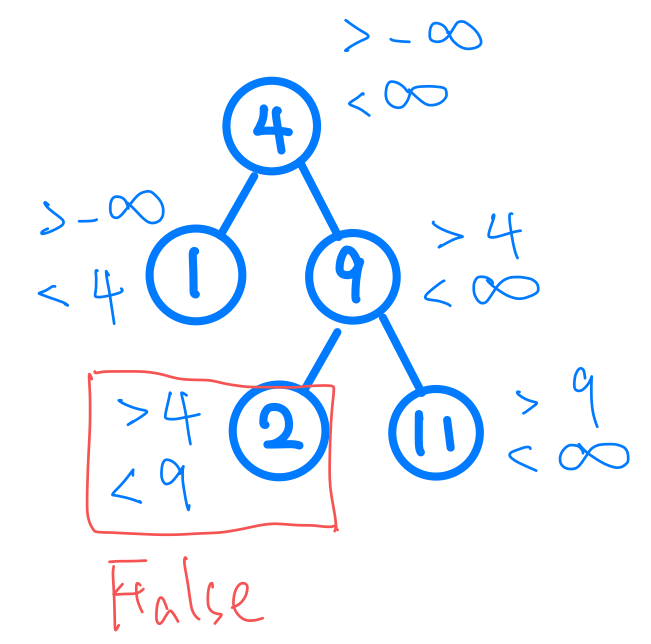

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:

        def dfs(node, minimum, maximum):
            if not node:
                return True
            if not (node.val < maximum and node.val > minimum):
                return False
            
            left = dfs(node.left, minimum, node.val)
            right = dfs(node.right, node.val, maximum)
            
            return left and right

        return dfs(root, -math.inf, math.inf)