「生活就像一盒巧克力；你永遠都不知道下一顆是什麼味道」《阿甘正傳》

• 第21天要來針對 CVE-2022-21449 的背後原理 - 橢圓加密簽章法做理解跟運算了。今天完全不需要寫程式跟用到環境，說不定用紙筆就夠了，是不是很高興呢?

• 所謂的橢圓曲線密碼學（英語：Elliptic Curve Cryptography，縮寫：ECC）是一種基於橢圓曲線數學的公開密鑰加密演算法。它的優點在於可以透過較短的金鑰提供同等效果的加密安全強度。但橢圓曲線最難理解的部分是它本身數系運算方式，其中的加法跟乘法都跟平常認知的不同，以下我們就會開始進行相關的說明。

• 首先要進行橢圓曲線世界的加法，要先準備好一條橢圓曲線 ，公式為 y^2 = x^3 + ax + b ，接下來的計算部分我都會透過 Elliptic Curve point addition 來做示範。

步驟如下 :

1. 測試橢圓曲線加法
   
2. 測試橢圓曲線乘法
   
   

• 大概了解它獨特的運算後，為了實際能夠運作在真實資料上，之後會使用有Fp的版本來做加法跟乘法的運算。也可參考 Day 24. 非對稱式加密演算法 - 橢圓曲線密碼學 Elliptic Curve Cryptography , ECC (觀念篇) 部分，我們這裡就使用它內文的圖表來做之後的運算。

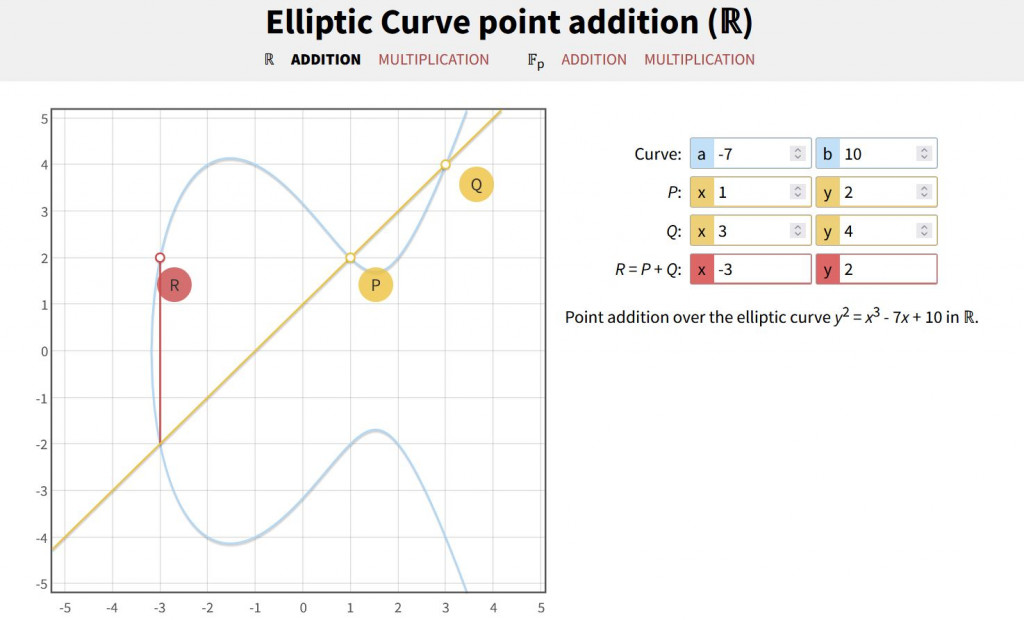
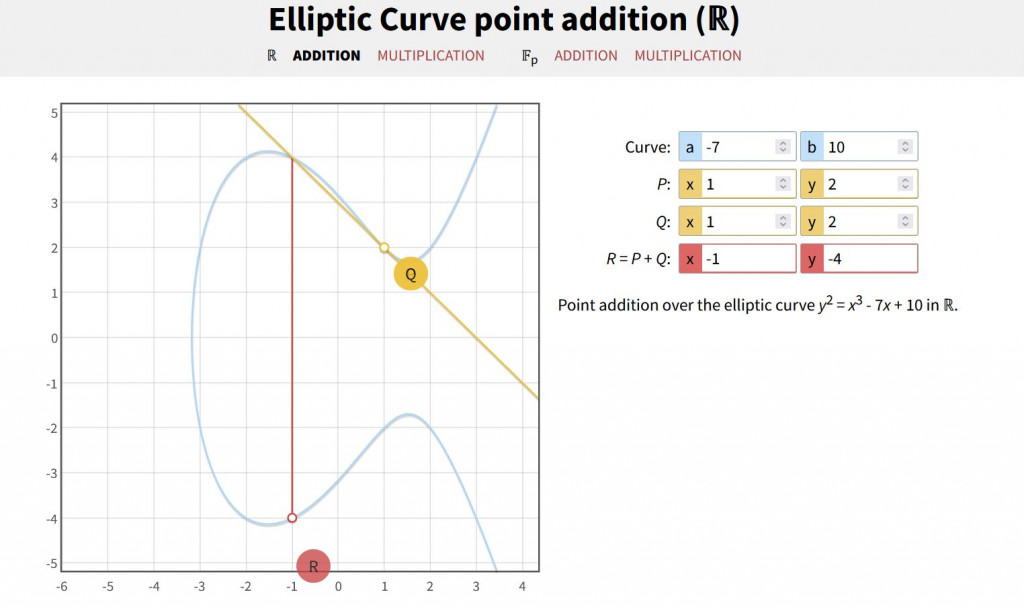
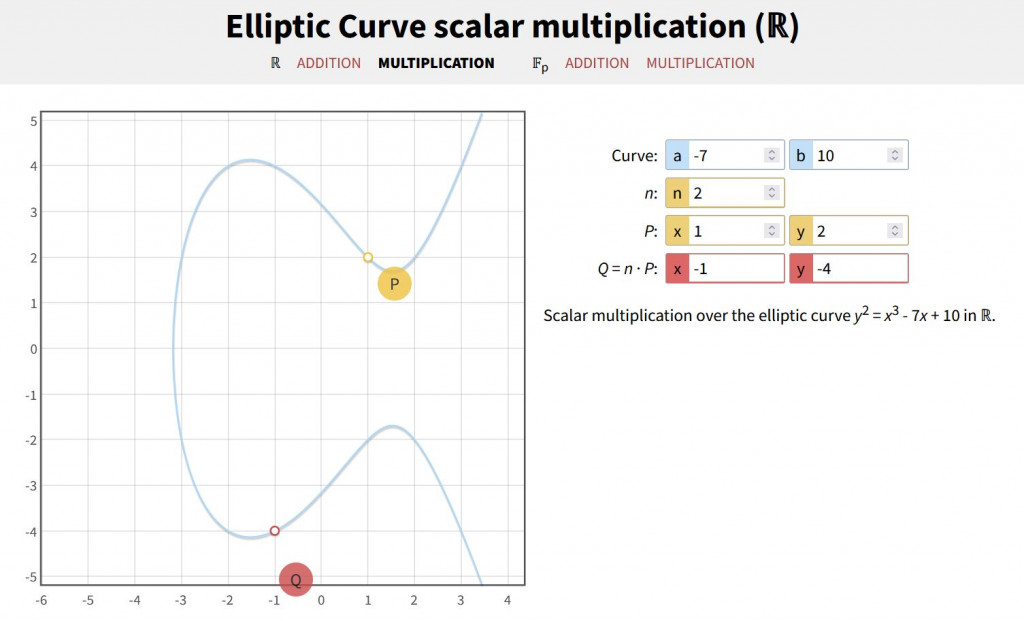
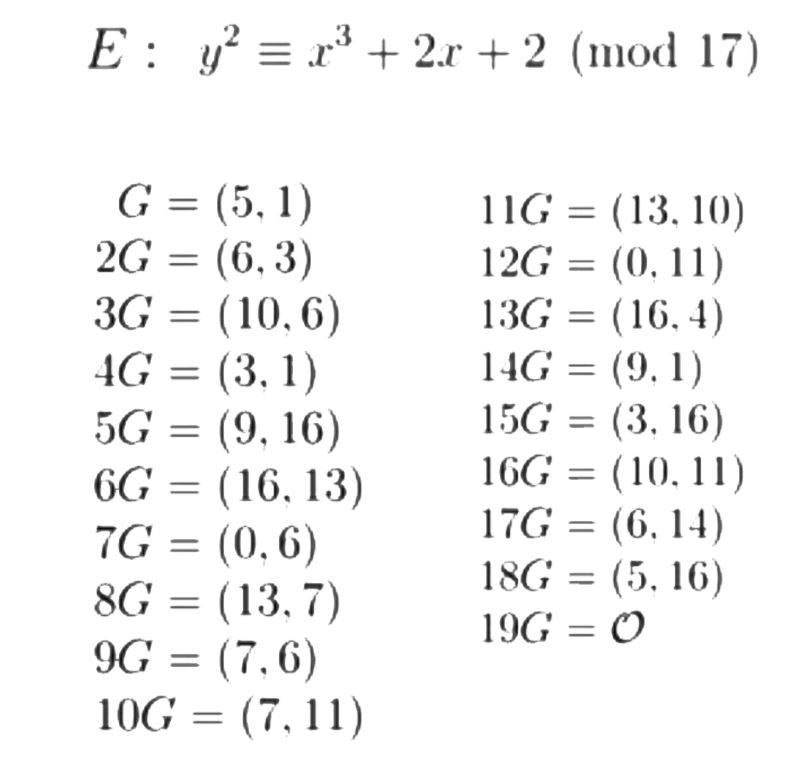
• 接下來要討論簽章驗章部分。之前有提過非對稱式要產生一組金鑰對，這邊也很特別，給定一數字 k，跟基點 G 計算 K = kG ，則這邊的私鑰就是 k ，公鑰就是 K。特別之處在於 k 是一維，而 K 是二維。比方說以上圖乘法來看，k=2，G=(5,1)，K=(6,3)

• 有了橢圓曲線定義的公私鑰之後，接下來就可以進行簽章、驗章的運算，這邊則是參考 Signing with ECDSA 的演算法進行運算，詳細計算可以參考我之前的影片 眼前的加不是加，你說的乘是甚麼乘?? 透過CVE-2022-21449 漏洞來了解 橢圓曲線簽章演算法計算方式 (Psychic Signatures)。 以下是相關計算結果。

• 每次看完都覺得數學好難，光要會運算就要花很多時間，更別提背後的數學意義。但問題來了，當(r,s) = (0,0) 會發生甚麼事情呢? 在計算 s^-1 的時候 Java 是透過 費馬小定理來運算，參考資料內的圖片如下 :

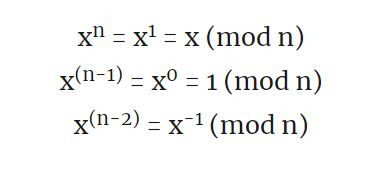
• 也就是說當 s=0， Java 其實是計算 s^(n-2) = 0 當作是 s^-1 的數值，導致後面一堆計算出來結果為 0，在跟帶入的 r=0 相比，自然會得到相等的結果。

• 終於到了尾聲了，數學的部分就只出現在這次文章中，下次則是要開始說這個漏洞在實際案例上的使用會長甚麼樣子。

參考資料 :

1. Day 24. 非對稱式加密演算法 - 橢圓曲線密碼學 Elliptic Curve Cryptography , ECC (觀念篇)
2. Elliptic Curve Cryptography: a gentle introduction
3. Elliptic Curve point addition
4. Elliptic Curve Cryptography: ECDH and ECDSA