繼第 8 天的「19. Remove Nth Node From End of List」，今天來解 這題！還沒看過第 8 天或再之前天數的朋友，歡迎也去看看~

話不多說，我們開始吧！

基本資訊

• 難度： Medium
• 網址： https://leetcode.com/problems/rotate-image

演算法與資料結構

• Matrix

題意

給予一個 n x n 的二維陣列，請順時鐘旋轉 90 度。

請直接修改傳入的二維陣列，運算途中不得宣告新的二維陣列。

範例

[[1,2,3],   [[7,4,1],
 [4,5,6], -> [8,5,2],
 [7,8,9]]    [9,6,3]]

矩陣旋轉

在線性代數裡面，向右旋轉90度矩陣為

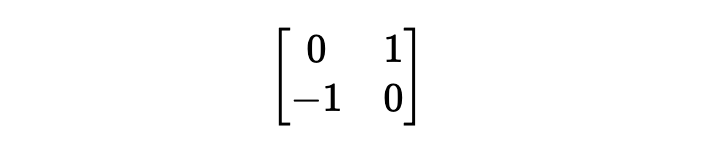
來自 轉置 和 水平反射 的相乘：

轉置

轉置矩陣為行列交換：

水平反射

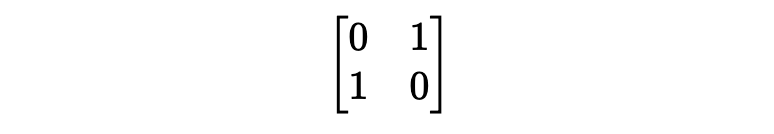
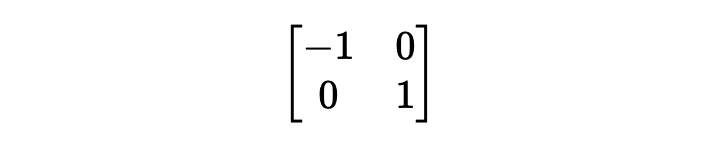
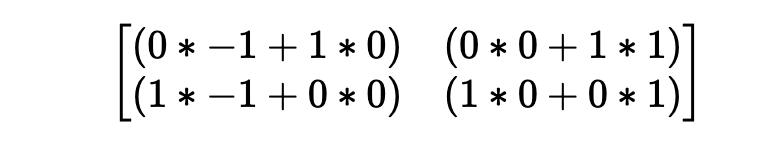
兩者相乘即可得出旋轉矩陣

得

實作

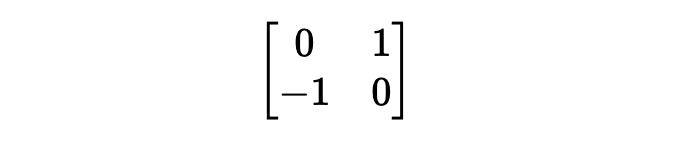
根據以上證明，在實作的時候就可以進行下列兩步驟

1. 轉置 / 行列交換
2. 水平反射 / 水平翻轉

以這個為例

1 2
3 4

1. 轉置 / 行列交換

先進行轉置，轉置完後為：

1 3
2 4

也就是說

• 當 row == column 的時候不交換
• 不相等的時候 matrix[row][column] 和 matrix[column][row] 交換

2. 水平反射 / 水平翻轉

進行翻轉之後就會得到最後結果：

3 1
4 2

在這一個階段的運算會進行

• row 維持不變
• 找到另一半邊的 column - columns 數減當前 column
• swap

程式碼

接著就可以開始寫程式碼了：

class Solution {
    func rotate(_ matrix: inout [[Int]]) {
        let numberOfRows = matrix.count
        
        // 轉置
        for row in 0..<numberOfRows {
            for column in row..<numberOfRows {
                let temp = matrix[row][column]
                matrix[row][column] = matrix[column][row]
                matrix[column][row] = temp
            }
        }
        
        // 水平反射
        for row in 0..<numberOfRows {
            for column in 0..<(numberOfRows/2) {
                let newColumn = numberOfRows - 1 - column
                let temp = matrix[row][column]
                matrix[row][column] = matrix[row][newColumn]
                matrix[row][newColumn] = temp
            }
        }
    }
}

執行結果

• Runtime: 4ms (Beats 96.99%)
• Memory: 14MB (Beats 51.88%)

複雜度分析

資料集為 n x n ，令 m 為 n x n 的總數。

結語

如果有什麼問題和回饋歡迎留言一起討論，

今天就到這裡，明天見！