集合 ( set ) 就像是「只有鍵,沒有值」的字典,一個集合裡所有的鍵都不會重複,因為集合不會包含重複的資料的特性,常用來進行去除重複的字元、或判斷元素間是否有交集、聯集或差集之類的關聯性。
原文參考:集合 set
本篇使用的 Python 版本為 3.7.12,所有範例可使用 Google Colab 實作,不用安裝任何軟體 ( 參考:使用 Google Colab )
集合由「數字、字串或布林」所組成,同一個集合裡的項目,可以是不同的型別,建立集合有兩種方式:
set()
使用 set() 可以建立空集合,或將串列、tuple、字串或字典轉換為集合,使用的方法為「set(要變成集合的元素)」。
如果建立時出現重複的項目,只會保留一個,如果是字典,只會保留鍵,如果是布林,True 等同 1,False 等同 0。
a = set()
b = set([1,2,3,4,5,1,2,3,4,5])
c = set({'x':1,'y':2,'z':3})
d = set('hello')
print(a) # set()
print(b) # {1, 2, 3, 4, 5} 只留下不重複的部分
print(c) # {'x', 'y', 'z'} 如果是字典,只保留鍵
print(d) # {'l', 'o', 'h', 'e'} 只留下不重複的部分
大括號 {}
如果不是空集合,可以使用「{項目}」建立集合 ( 單純寫大括號,會變成「空字典」 )。
a = {0,1,2,3,'a','b',False}
print(a) # {0, 1, 2, 3, 'a', 'b'} False 等同於 0,所以只保留 0
使用「集合.add(項目)」可以將某個項目加入集合中,下面的程式會將 x 和 y 兩個文字加入 a 集合。
a = {0,1,2,3,4,5}
a.add('x')
a.add('y')
print(a) # {0, 1, 2, 3, 4, 5, 'x', 'y'}
有兩種方法可以移除集合裡的某個項目:
remove()
使用「集合.remove(項目)」,可以將指定的項目移除,不過如果該項目不存在,就會執行錯誤。
a = {0,1,2,3,'x','y','z'}
a.remove('x')
print(a) # {0, 1, 2, 3, 'y', 'z'}
discard()
如果不希望在移除項目時發生執行錯誤的狀況,可以使用「集合.discard(項目)」,將指定項目移除
a = {0,1,2,3,'x','y','z'}
a.discard('x')
a.discard('a') # 不會發生錯誤
print(a) # {0, 1, 2, 3, 'y', 'z'}
集合有四種運算型態,分別是「交集、聯集、差集、對稱差集」,透過下圖可以了解四種運算型態。
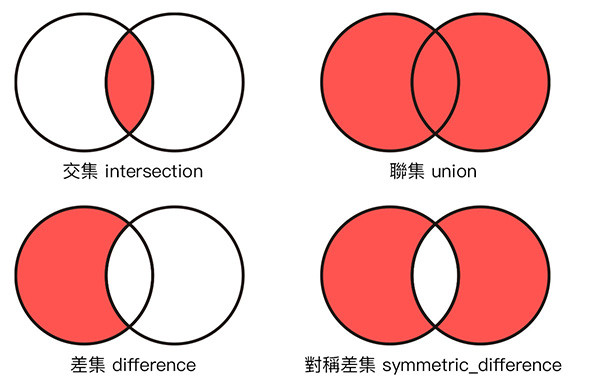
使用集合運算有兩種方法,一種是使用特定的方法,另外一種則是使用「符號」( 集合運算子 )
| 集合 | 方法 | 運算子 |
|---|---|---|
| 交集 | a.intersection(b) | a&b |
| 聯集 | a.union(b) | a|b |
| 差集 | a.difference(b) | a-b |
| 對稱差集 | a.symmetric_difference(b) | a^b |
下方的程式,會呈現進行 a 對 b 進行集合運算後的結果。
a = {1,2,3,4,5}
b = {3,4,5,6,7}
# 交集
print(a.intersection(b)) # {3, 4, 5}
print(a&b) # {3, 4, 5}
# 聯集
print(a.union(b)) # {1, 2, 3, 4, 5, 6, 7}
print(a|b) # {1, 2, 3, 4, 5, 6, 7}
# 差集
print(a.difference(b)) # {1, 2}
print(a-b) # {1, 2}
# 對稱差集
print(a.symmetric_difference(b)) # {1, 2, 6, 7}
print(a^b) # {1, 2, 6, 7}
假設有 A、B 兩個集合,超集合和子集合的關係可以參考下圖:
| 集合 | 說明 |
|---|---|
| 超集合 | A 完全包含 B,A 和 B 所包含的元素可能完全相同 |
| 真超集合 | A 完全包含 B,且具有 B 沒有的的元素 |
| 子集合 | B 完全被 A 包含,A 和 B 所包含的元素可能完全相同 |
| 真子集合 | B 完全被 A 包含,且 A 具有 B 沒有的的元素 |
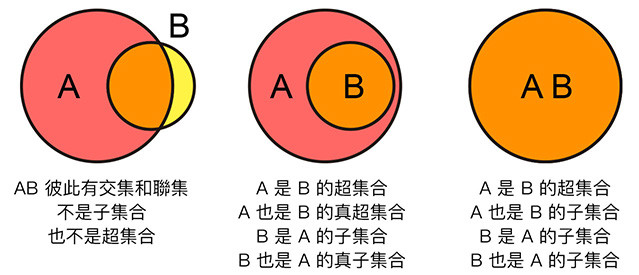
下面的程式列出四個集合,使用「大於、小於、等於」可以呈現彼此的關係,從印出的結果可以看到各個集合之間的關係。
a = {1,2,3,4,5,6,7}
b = {3,4,5,6,7}
c = {1,2,3,4,5,6,7}
d = {6,7,8,9}
print(a<=a) # True 自己是自己的子集合
print(b<=a) # True b 是 a 的子集合
print(b<a) # True b 也是 a 的真子集合 ( 因爲沒有等於,完全包含 )
print(c<=a) # True c 是 a 的子集合
print(a<=c) # True a 也是 c 的子集合
print(d<a) # False d 和 a 沒有子集合或超集合關係
此外,使用「b.issubset(a)」方法可以檢測 b 是否為 a 的子集合、「a.issuperset(b)」方法可以檢測 a 是否為 b 的超集合。
a = {1,2,3,4,5,6,7}
b = {3,4,5,6,7}
c = {1,2,3,4,5,6,7}
d = {6,7,8,9}
print(b.issubset(a)) # True b 是 a 的子集合
print(a.issuperset(b)) # True a 是 b 的超集合
print(c.issubset(a)) # True c 是 a 的子集合
print(d.issubset(a)) # Fasle d 不是 a 的子集合
使用「len(集合)」可以回傳某個集合的長度 ( 有幾個元素 )。
a = {1,2,3,4,5,6,7}
print(len(a)) # 7
使用「元素 in 集合」可以檢查集合中是否存在某個元素,如果存在就是 True,不存在就是 False ( 使用「元素 not in 集合」可以判斷不存在 )。
a = {'a','b','c','d',1,2,3}
print('b' in a) # True
print(2 in a) # True
print(99 in a) # False
大家好,我是 OXXO,是個即將邁入中年的斜槓青年,我有個超過一千篇教學的 STEAM 教育學習網,有興趣可以參考下方連結呦~ ^_^
