電子簽章

雜湊函數最著名的應用就是進行電子簽章

回顧前幾天談到的公鑰加密也可以進行電子簽章，Alice用私鑰將明文M加密傳給Bob，Bob可用Alice所發佈之公鑰將密文還原，確認該明文為Alice所授權

不過當M很大時，用私鑰將其加密計算需要花很長時間，同時傳輸相當大的密文與明文的過程也須很大的頻寬，很耗費資源

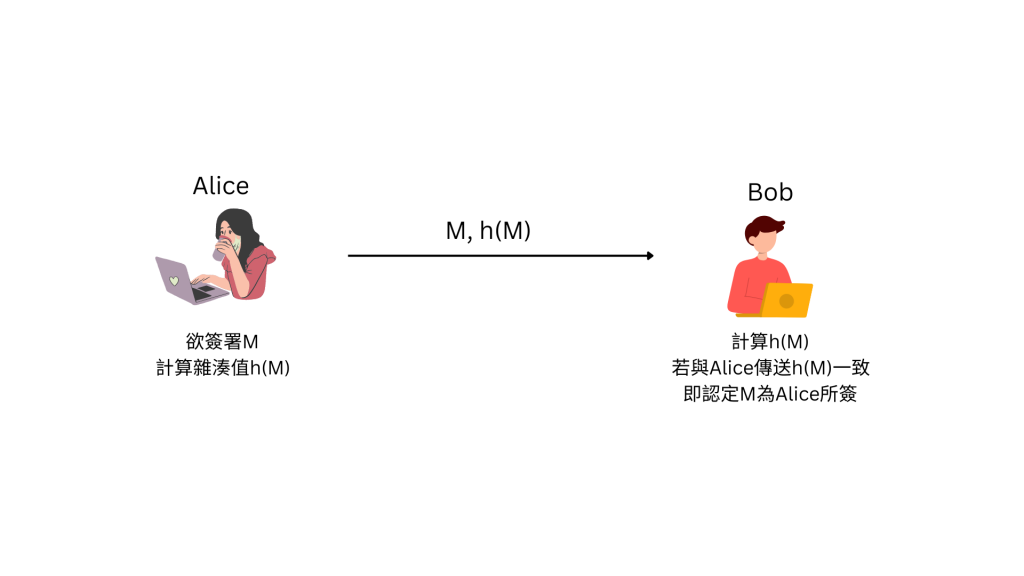
使用雜湊函數會讓這一切方便地多，Alice可以將很大的M送進雜湊函數中得到較小的S，並將M與S一同傳輸給Bob，Bob可以自己執行雜湊函數將M轉換檢查是否為S

根據雜湊函數的特性，Bob收到的明文需與Alice的明文相同，否則兩雜湊值會不同，藉此確認該明文確實由Alice所簽署

線上競標

假設Alice, Bob, Charlie三人欲參與線上競標

三人上繳自己提出的買價，由出價高者得標
由於三人對彼此以及對競標系統不信任，例如Alice擔心競標系統在她上傳買價後意外或故意將其買價洩露給對手；又或者Alice上傳買價100元、Bob上傳買價120元後，Charlie利用系統漏洞得知此二資訊後，出價121元得標

因為這些問題的考量，三方都不願當前兩個競標的人

有鑒於這些考量，競標平台可以請三方上傳自己價格的雜湊值
當收到所有的雜湊值後，平台會公布雜湊值，並要求三方公佈自己的真實競標價格作為驗證

由於攔截給平台的雜湊值得不到任何資訊，以上的不信任問題也得以被解決

減少垃圾郵件

這邊定義不需花費太多努力生產(CPU計算量)的郵件為垃圾郵件

我們可以利用雜湊函數的特性減少一方傳送垃圾郵件的數量

給定要傳送的文件本體M(包括寄件者與收件者地址)以及當前時間T，寄送者必須找出一個數值R使得
h(M, R, T) = (0, ..., 0, X)，使得生成出的雜湊值前面有N個0
此R找到方能寄出(M,R,T)，收件者一方只需驗證這三者生成的雜湊值前面有N個0即可

和加密貨幣的挖礦類似，都是一種工作量證明(proof-of-work)系統

寄件方平均而言得嘗試 個R，而接收方只需計算1次雜湊函數而已，如此增加寄件方的寄件成本

對於N=40是個對一般寄件者份量還算輕鬆的計算量，但是對垃圾信件來說計算成本相當昂貴，收件者可以調整N的大小來決定寄件方所需做的努力來控制接收垃圾郵件的頻率