今天我們來算個數學

生日問題1

我們從小到大應該都會遇到一些人，很巧合地與自己同一天生日
想像今天大家在同一間教室，請問教室至少要多少人，才能使你遇到跟你同一天生日的人的機率大於50%呢？

如果高中數學還記得的讀者可以先自己試試看

數學計算

至少遇到一人生日與你同一天的機率，就是全部扣去大家都跟你不同天的機率，因此可得到，稍微按個計算機可以得到N至少253人

機率詮釋

有時候如果遇到太難算的機率問題可以交由模擬的方式來處理

由於每次遇到的人是隨機，無法保證每次都能找到與你相同生日的人

機率的意思，可以想像成千上萬個平行宇宙的你正在進行這個實驗，我們在每個宇宙中隨便找N個人到某間教室，每個宇宙的你在同一個瞬間打開了教室的門，並尋找是否有人與你生日同一天，若有則回報1；無則回報0

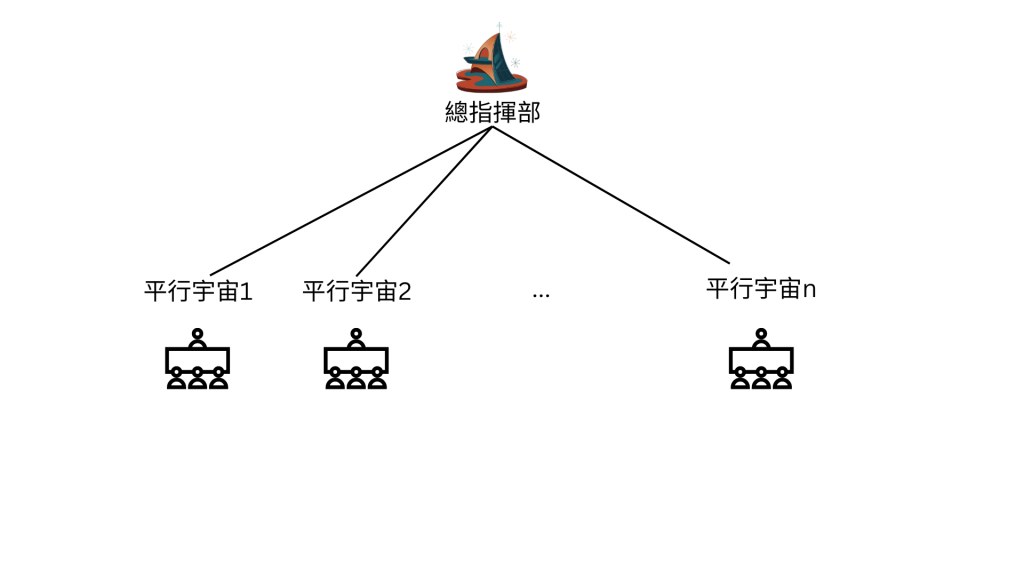
等到收到所有的回報後，指揮部將計算其 比例，此比例即為這個事件發生之機率（這是根據事件發生頻率，結合大數法則的一種詮釋方式，還有很多種詮釋機率的方式）

以下我用模擬的方式來求事件發生之機率

import numpy as np

my_birthday = 1
n = 10_000

N = 253

X = np.random.randint(0, 365, size=(N, n))

probability = np.any(X == my_birthday, axis=0).mean()

print('probability = {:.2f} for N = {}'.format(probability, N))

各位可以調整N的大小來得出不同班級人數，存在與自己生日同一天人的機率

生日問題2

第二個生日問題就沒那麼容易了

請問班上至少幾人，才能讓至少有兩人生日同一天的機率超過50%？

數學的部分交給各位來算😎

以下呈現模擬的程式：

n = 10_000

N = 23


X = np.random.randint(0, 365, size=(N, n))


def if_duplicate(a):
    if len(list(set(a))) != len(a): return True
    return False

probability = np.apply_along_axis(if_duplicate, 0, X).mean()

print('probability = {:.2f} for N = {}'.format(probability, N))

可以看到，只要23人，就有50%以上的機率班上有兩人同一天生日，各位可以找找N多少可以讓配對發現的機率到90%

這數字少得有點違背直覺，因此這個問題又稱為生日悖論

各位可以想想問題出在哪裡

這邊提供給各位一個小直覺，想讓會產生n個隨機的值可以命中，大概要進行n次比較

如生日問題1，班上有N個同學，只能提供N次與正確答案的比較，因此N需要與365差不多的數字

生日問題2中，班上N個同學可提供N(N-1)/2約N平方組比較，因此 解得N大約19左右即可找到配對

與雜湊函數的關係

有關以上生日函數的啟示，假設有一個會產生N位元的雜湊函數，至少需比較
個數字便有50%的機會找到兩個不同的東西產生相同雜湊值 (就跟班上至少幾人可以找到兩個同一天生日一樣，只要根號等級的個數即可)

相比於N位元的對稱密鑰，平均得嘗試 才可命中(這也可以用算的，給各位當小練習😎)

因此，雜湊函數所生成的位元數必須為對稱密鑰的兩倍，方能達到相同的安全效果

生日攻擊

若雜湊函數的輸出位元不夠多，便有可能遭受攻擊

回憶雜湊函數的電子簽章方式：
Alice利用雜湊函數h進行電子簽章，先計算明文M雜湊值S，再將n位元的雜湊值用自己的私鑰加密得到[S]
最後，將加密的雜湊值[S]與明文M傳送給Bob

要驗證簽章，Bob用Alice發布的公鑰解密[S]，並檢查是否與S一致藉此認證為Alice所簽名

假設Trudy想要讓Alice簽名邪惡的訊息E(叫Alice給Trudy錢之類的)，他可以利用以下手法進行攻擊：

• Trudy先製造一個Alice可能願意簽名的無害訊息I(偽裝成Alice例常收到的郵件)
• Trudy製造 個很像I的訊息，每一個都改一點其中的文字、符號，使其整體文意不變
• 同樣生成 個邪惡訊息，每個都與E文意相同，只是稍微改其中文字而已
• Trudy將 個I的變種與 個E的變種丟入雜湊函數計算，根據生日問題2，Trudy很有可能找的到兩個I與E的變種，其雜湊值相等
• Trudy將該變種I寄送給Alice，待其回傳I與私鑰加密後的[h(I)]給Trudy
• 由於[h(I)] = [h(E)]，Trudy便可憑藉變種E與Alice加密的雜湊值偽造Alice的簽名

以上的過程並非攻擊Alice的公鑰加密系統，而是利用暴力解攻擊雜湊函數h
為了避免此攻擊發生，實務上的雜湊函數輸出位元都足夠大，使得 大到無法全部計算