今日學習重點

訓練深度學習模型實質上就是計算答案與優化答案的過程，在此過程中常常涉及許多複雜的計算，而在今天我們將探討深度學習能自動抽取特徵的原因以及講講整個模型訓練的過程，今日的學習重點如下:

1. 學習深度神經網路(Deep Neural Networks, DNN)的原理
2. 理解前向傳播(Forward Propagation)與反向傳播(Backward Propagation)的目的
3. 認識優化器(Optimizer)、學習率(Learning rate)、損失值(Loss)之間的關係。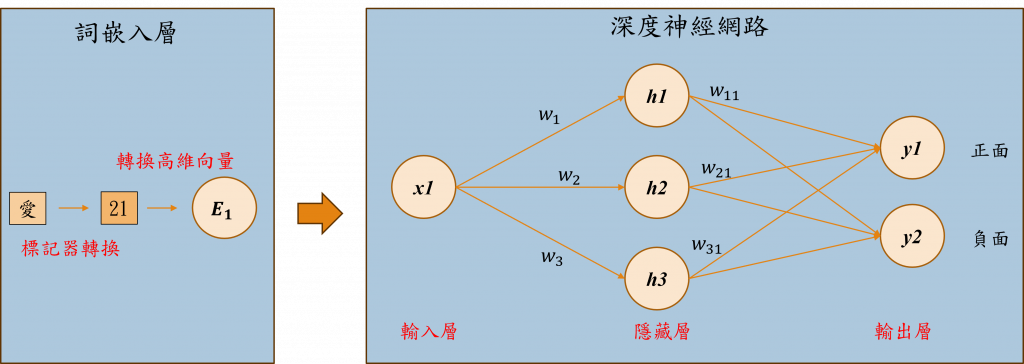

深度神經網路(Deep Neural Networks, DNN)

深度神經網路（Deep Neural Networks，DNN）是一種多層感知器（Multilayer Perceptron，MLP），由多層神經元（Neuron）組成。其目的是跨越不斷調整神經元之間的權重（Weight）來模仿人類大腦的功能。這種結構能夠自動學習複雜的輸入特徵和模式，以進行對未知資料的分類或預測。在上圖中的範例是通過創建1維的詞嵌入向量來進行深度神經網路的運算，使其能夠分類出該單字是正面評價還是負面評價的。

小提示:
通常詞嵌入層的維度都會是高維向量(BERT是768維)，在這裡使用1維的目的是為了方便後續的公式理解。

深度神經網路主要由三個部分組成，分別是輸入層(input layer)、隱藏層(hidden layer)以及輸出層(output layer)。其中隱藏層越多層能處理的輸入資料也就越複雜。但要注意的是，如果處理的資料相對簡單，那麼使用較少的隱藏層，模型的效果會更好。接下來讓我們深入了解這三個部分的各自角色。

輸入層(input layer)

深度神經網路的第一層被稱作輸入層，該層的主要目的是獲取外部數值資料，如在進行文字分類時，我們會將詞嵌入層的資料傳送至此。在這層中並無特殊的計算公式，僅負責將資料傳送至下一層。

隱藏層(hidden layer)

隱藏層是深度神經網路的關鍵部分，該層接收特徵x1、x2、x3...xn的輸入，並透過和各隱藏層中的權重w1、w2、w3...wn進行運算，來計算出每個隱藏層神經元的結果。以上圖為例各神經元的計算結果h1 = x1w1、h2 = x1w2、h3 = x1w3。當有了h1、h2、h3的值之後，我們就可以根據這些數據來算出模型的整體輸出結果。

輸出層(output layer)

當隱藏層將資料傳遞給輸出層後，該層會透過h1、h2、h3來計算出模型的結果，也就是y1 = h1w11 + h2w21+ h3w31的結果，這個結果便是模型預測的機率。這樣解釋可能不夠清楚，假設正面評價的標籤是y1，那麼y1的輸出結果應該更接近1；若反面評價的標籤是y2，那麼y2的輸出結果就應該更接近於0。如此一來我們就能夠根據最終的輸出y1、y2的結果來判斷最有可能的情況。

在以上的步驟中也就是深度學習的前向傳播(Forward Propagation)過程，所以我們也可以說前向傳播是模型計算結果的過程。

模型該怎麼修正輸出結果

在任何神經網路裡，兩個步驟都是不可或缺的，它們分別是前向傳播與反向傳播(Backward Propagation)，而我們已經掌握了前向傳播的概念，接下來需要解析的則是反向傳播的過程，此部分將會被分成以下幾步：

【STEP 1 對最後一層輸出進行Softmax】

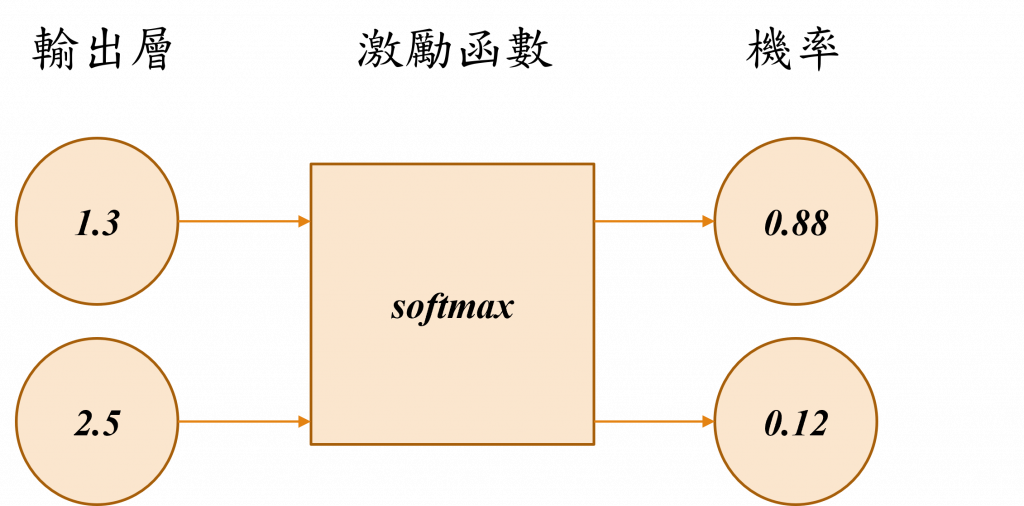
首先我們需要透過損失函數(Loss Function)來計算出模型在這次運算中的損失值，如同我們在前面的小節所提到的，輸出層的結果是模型的機率輸出，這需要透過名為Softmax的激勵函數(Activation Function)進行轉換，該函數能將輸出層的數字轉換為機率值，這個步驟的目的就是為了更精確地計算模型的損失值。

小提示
激勵函數是一種在模型不同層中所使用的數學函數，該函數的目的是為了將計算出來的線性結果轉換成非線性，這樣做的原因是因為現實中的數據通常是以非線性呈現的，因此我們加入激勵函數能夠使計算結果更符合現實。

【STEP 2 計算模型的損失】

接著我們就能夠通過該方式計算模型的損失，最簡單的計算模型方式，就是計算標籤(Lable)與預測機率的誤差。

這時我們能先將標籤進行One-Hot Encoding轉換的動作，讓正面評價的標籤為[1, 0]，並假設預測輸出是[0.88, 0.12]，那麼在計算模型的損失時，我們可以直接算出|1 - 0.88| + |0 - 0.12| = 0.24的損失結果。

小提示:
在前幾天，我們提到One-Hot Encoding在自然語言處理上的問題，這是針對詞彙轉換成向量時可能會遇到的問題，而這次我們選擇使用詞嵌入來進行詞彙轉換，而One-Hot Encoding則用於標籤的轉換過程。

【STEP 3 計算輸出層梯度】

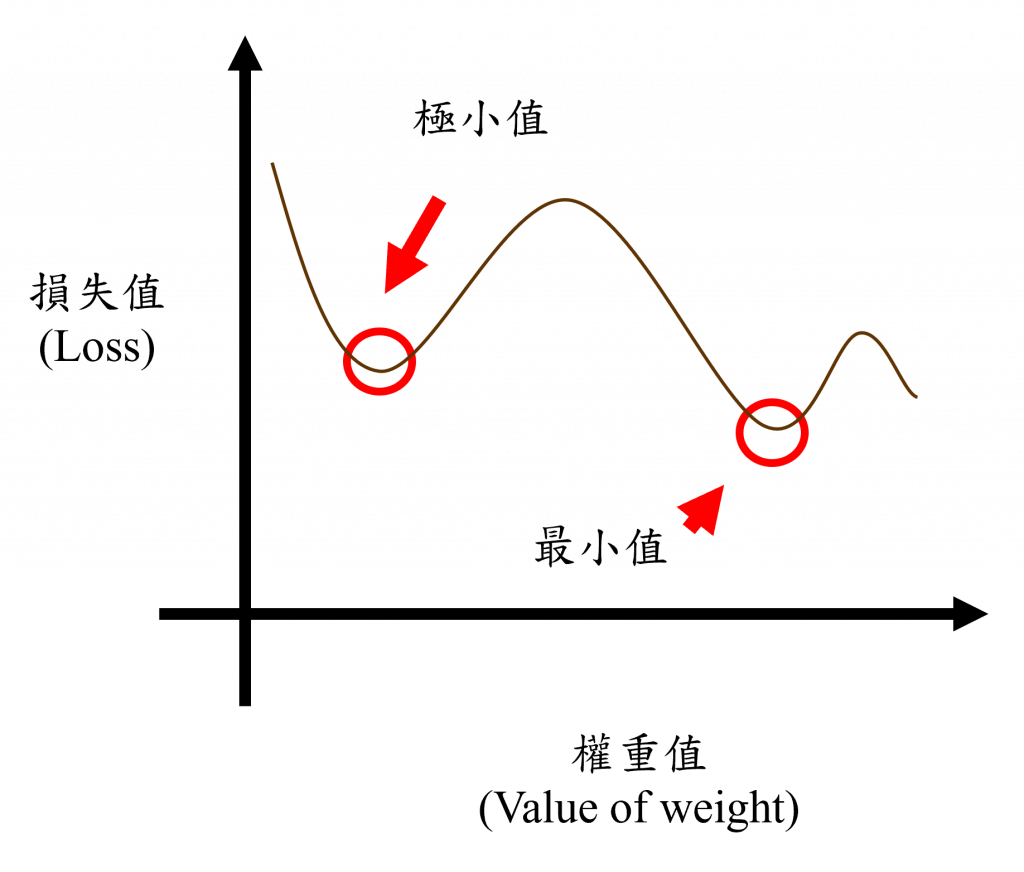
我們現在來到最困難的部分，那就是計算神經元梯度的過程，而我們計算梯度的目的就是為了找到各神經元的變化方向，以幫助我們找到最小值或極小值，而計算的第一步進行我們需要找到損失函數L對輸出層的輸出的梯度。

假設輸出層有n個神經元，我們計算每個神經元的梯度為:

其中ai(L)是輸出層的第i個神經元的輸出。

【STEP 4 計算隱藏層梯度】

接下來，我們需將梯度向後傳播至隱藏層，以計算出每一層的梯度，在這步驟我們可以透過輸出層梯度進行連鎖率運算，我們便可以得出第L層中第i個神經元的梯度。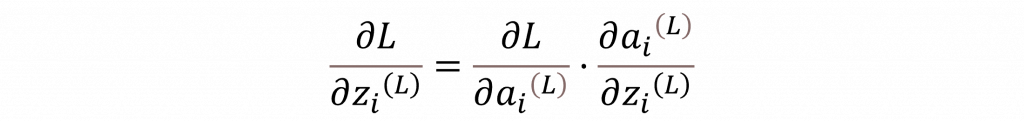

這樣就會一直將梯度傳播到上一層的神經元，重複這個過程，直到計算出輸入層的梯度為止。

【STEP 5 計算各權重梯度】

最後我們可以計算每個權重的梯度，對於連接第L-1層第j個神經元與第L層第i個神經元的權重，我們可以透過以下公式來進行計算。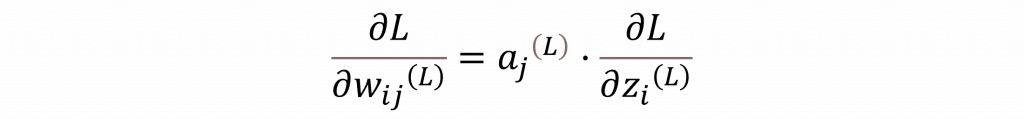

【STEP 6 更新權重】

當我們計算出各權重的梯度後，我們就能得知該曲線的變化程度，這時我們可以選擇使用梯度下降法(Gradient Descent)或其他優化器(Optimizer)來更新權重，以降低損失函數的數值。對於梯度下降法的更新規則，如下所示：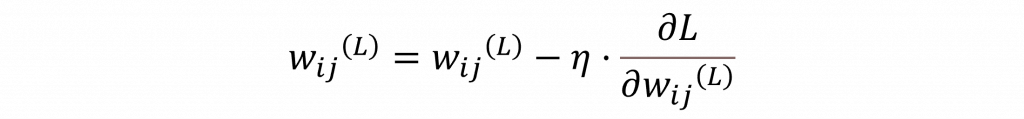

其中𝜂代表的是學習率，這是用來調整移動速率的值，若該值設定過大，會導致無法收斂的狀況。因此在大多數的優化器中，該值通常只設定為1e-3。

不過你可能聽到這裡會有些不太了解的地方，所以我在這裡簡單把整個訓練過程說明一遍：首先我們會通過模型計算結果(前向傳播)，接下來透過損失函數計算目標與預測結果的誤差，然後反向傳播計算各神經元的梯度，最後透過優化器調整權重。

按照這個過程來，模型將能夠不斷地通過調整權重的方式降低模型的損失值，以期算出最佳的目標，這就是我們所說的訓練模型實際上正在進行的動作，而在不同後神經網路中，不外乎都是通過這種方式進行訓練的。

後話

今天我們已經坦討並說明了在深度學習中會使用的一些數學公式，同時解釋了深度神經網路的模型架構，而在明天的內容中我將利用Pytorch程式碼來向你示範該如何使用深度神經網路訓練出我們在第三天所使用的詞嵌入層權重。

那麼我們明天再見！

內容中的程式碼都能從我的GitHub上取得:
https://github.com/AUSTIN2526/iThome2023-learn-NLP-in-30-days