昨天我們談了 Classification，並且講述可以透過 Logistic Regression 來解決這個問題。不過昨天並沒有講到的是關於模型的選擇，今天小小提一下。

雖然原則上我們會採用 Sigmoid Function 來作為模型的基礎，不過其實你可以自行決定 的長相。

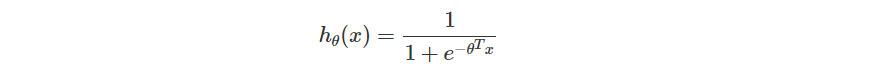
也就是說如同過去的 Regression 問題你可以自己決定要 , 之類的模型，在這裡你同樣也可以這樣做，而 Classification 不過是在這個 Polynomial 後面多連接一個 Sigmoid 而已。

Cars - Purchase Decision Dataset

今天我們會使用 Kaggle Cars - Purchase Decision Dataset 來練習簡單的 Classification。在這個 Dataset 當中包含了幾個 Column

• User ID: 單純的流水號
• Gender: 生理性別 (Male / Female)
• Age: 年齡
• AnnualSalary: 客戶年收入
• Purchased: 最後是否下單 (0 / 1)

由於流水號對於買不買可說是沒有關聯，所以這裡我就直接忽略這個欄位。而由於這次只想簡單描述只有兩個變因的情境，所以我挑選了 年齡 以及 客戶年收入 作為變因，而 最後是否下單 則為 label。

在開始之前

接下來的實作建議在 jupyter notebook 或是 Google Colab 當中運作會比較方便。

在接下來的實作我們會需要

• python3
  我使用的是 3.10 這個版本
• numpy
  我使用的是 1.23.5 這個版本
• matplotlib
  我使用的是 3.5.1 這個版本
• pandas
  我使用的是 2.0.1 這個版本

開始實作

一如既往，我們大致上會歷經三個步驟

1. 定義函數
2. 將資料輸入進模型，並評估模型好壞
3. 調整參數大小

函數的部分我們有 Sigmoid，而搭配的線性函數則是單純的 ，以更簡單的形式來描述是 。

那麼接下來就進入正題吧！

引入函式庫、讀取資料

這次同樣會使用到 numpy、matplotlib、pandas 和 seaborn。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

接下來將資料讀取進來。

data = pd.read_csv('car_data.csv')
labels = ['Age', 'AnnualSalary', 'Purchased']
m = data.shape[0]
!mkdir -p res

之後我會想把每個階段預測出來的 boundary 做成圖，放在 res 資料夾當中，所以這裡有一個 mkdir 指令。
不過如果你並不是在 jupyter 或是 colab 上運行則可以直接忽略這行。

切割參數

接下來我們要把切成我們想要的 。特別的是，我們在這裡還把 標準化了。

這是為了避免待會把資料丟進 Sigmoid 之後極小的數值會對應到趨近於零的數字，導致後續 log 的運算出現問題。

標準化也就是將資料扣除平均後除以標準差。

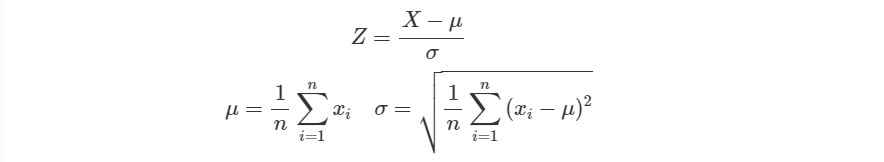
x0 = data[labels[0]].values.reshape(m, 1)
x1 = data[labels[1]].values.reshape(m, 1)
y = data[labels[-1]].values.reshape(m, 1)

x0 = (x0 - np.mean(x0)) / np.var(x0)
x1 = (x1 - np.mean(x1)) / np.var(x1)

製作矩陣 X

接下來我們要把 以及常數項的倍率 1 一起做成一個矩陣，後續就可以直接使用這個矩陣做運算。

X = np.append(x0, x1, axis=1) # 合併 x0 和 x1
X = np.append(X, np.ones((X.shape[0], 1)), axis=1) # 加上 1

資料分布

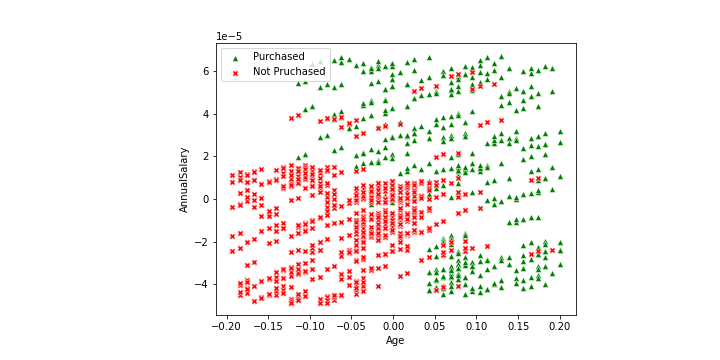
接下來試著先看一下資料的分布如何。基本上就是分成兩種狀況

1. 最終有購買的以綠色標記
2. 最終沒購買的以紅色標記

plt.figure(figsize=(10, 5))
plt.subplots_adjust(left=0.3, right=0.8)
sns.scatterplot(x = x0[y == 1],
                y = x1[y == 1],
                marker = "^",
                color = "green",
                label = "Purchased")
sns.scatterplot(x = x0[y == 0],
                y = x1[y == 0],
                marker = "X",
                color = "red",
                label = "Not Pruchased")
plt.xlabel(labels[0])
plt.ylabel(labels[1])
plt.savefig('scatter.png')
plt.show()

函數定義

首先定義一下 Sigmoid Function。

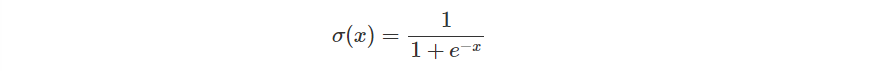
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

接下來定義一下 Loss Function。

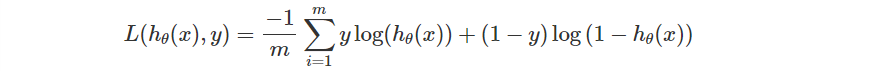
Losses = []
def Loss(x, y, theta):
    y_pred = sigmoid(np.dot(x, theta))
    return np.sum(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred)) / (-m)

再來是梯度的定義。

def gradient(x, y, theta):
    y_pred = sigmoid(np.dot(x, theta))
    return np.dot(x.T, (y_pred - y)) / m

最後為了後續畫圖方便，我把整個繪圖的功能寫成一個函數。基本上包含了三個部分。

1. 繪製有購買的標記
2. 繪製沒購買的標記
3. 繪製當前分割範圍

在分割這邊目前我還沒有找到一個好方法可以直接畫出直線，因此暫且先使用繪製梯度的方式來表示兩個不同的預測區域。

函數的定義會接入當前的 ，接著有一個 id 方便我們儲存多個圖片。

def draw(theta, id):

這一部分跟前面一樣，只是兩個 scatter plot。

sns.scatterplot(x = x0[y == 1],
                y = x1[y == 1],
                marker = "^",
                color = "green")
sns.scatterplot(x = x0[y == 0],
                y = x1[y == 0],
                marker = "X",
                color = "red")

在來繪製預測區域的部分，我選擇先取出我要繪製的範圍，也就是看 和 的最大最小值。接下來從中 sample 出 50 個間隔相同的點。

MIN_x, MAX_x = np.min(x0), np.max(x0)
MIN_y, MAX_y = np.min(x1), np.max(x1)

sample = 50
x_boundary = np.linspace(MIN_x, MAX_x, num=sample)
y_boundary = np.linspace(MIN_y, MAX_y, num=sample)

把全部的點對建立起來，待會函式庫就會幫我們去看過這些所有的區域。

xx, yy = np.meshgrid(x_boundary, y_boundary)

再來要提供的是每個點的預測結果，所以把全部的 和 以及常數倍率 1 都先合併在一起，就如同前面製作矩陣 一樣。

# 合併 xx, yy
x_plot = np.append(xx.flatten().reshape((sample**2, 1)), yy.flatten().reshape((sample**2, 1)), axis=1)
# 加上倍率
x_plot = np.append(x_plot, np.ones((x_plot.shape[0], 1)), axis=1)
# 預測結果若 > 0.5 則是預測有購買(1)，反之沒有(0)
y_plot = np.dot(x_plot, theta).reshape(xx.shape) > 0.5

最後就可以透過 contourf 來繪製圖片。

plt.contourf(xx, yy, y_plot, alpha=0.3)
plt.savefig(f'res/{id}.png')
plt.show()

設定 Hyperparameters

與以往相同，我們需要設定 epochs 、 learning rate 以及 參數初始值 。這裡我們設定的數值如下。

epochs = 30000
lr = 0.1
theta = np.zeros((2 + 1, 1))

更新參數

更新參數的邏輯也是相同的。

1. 計算 Loss
2. 計算 Gradient
3. 更新
4. 輸出訊息

特別的是我們會每 1000 個 epoch 輸出一次當前預測的圖片。

for i in range(epochs):
    loss = Loss(X, y, theta)
    d_theta = gradient(X, y, theta)
    theta -= lr * d_theta
    Losses.append(loss)
    print(f'epoch: {i}\tloss: {loss}')
    
    if(i % 1000 == 0):
        draw(theta, i // 1000)

觀察 Loss Function

在來通常會看一下 Loss Function 是否如同預期有好好的下降。

plt.plot([i for i in range(len(Losses))], Losses)
plt.show()

觀察結果

依照上面的參數去執行的話，你會得到的 Loss Function 應該會是這個樣子。

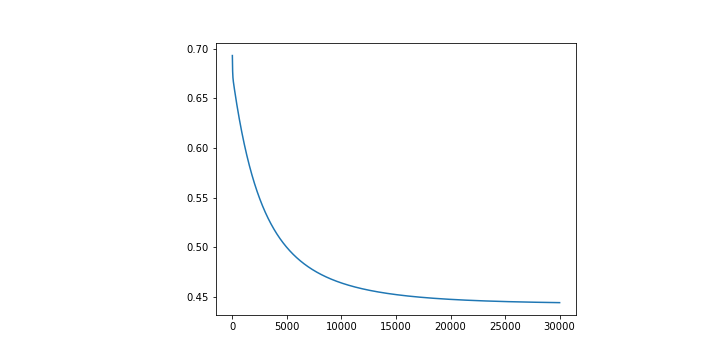
看起來是有穩定下降的。之所以會設定 30000 個 epochs 是因為大致上會在這個數字附近收斂而已。

在來當然要看的就是模型預測出來的結果如何，我們剛剛已經有在訓練的過程當中去輸出圖片了，後續我把它做成了 gif，可以更好的觀察更新的過程。

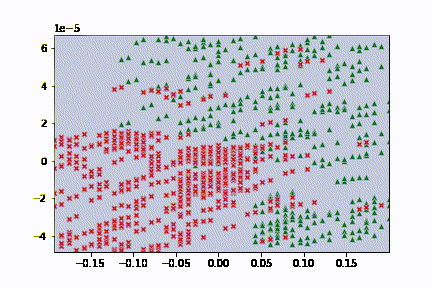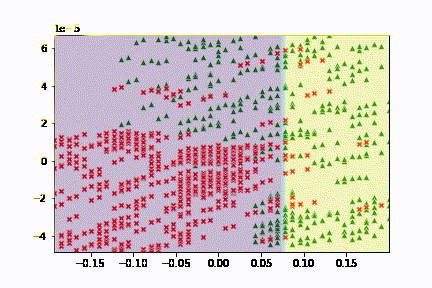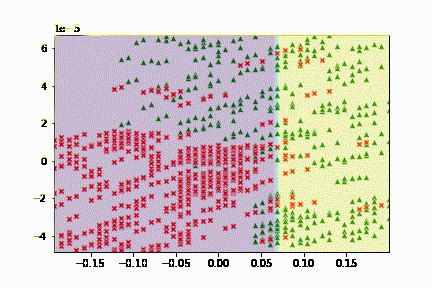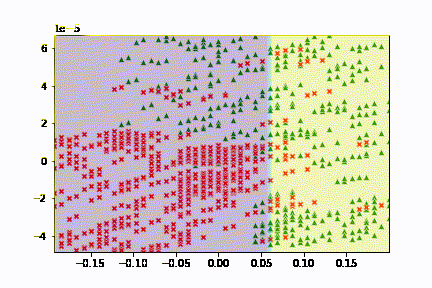
可以觀察到基本上可以觀察到函數的更新方向是固定的，不過畢竟線性能夠切出來的區域良莠還是有差，所以結果沒有想像中的還要理想。

有趣的是，你可以嘗試一些不同的初始值，也許你會看到的切法會長得不一樣。

最終實作的結果放在 Github 上，可以參考。

小結

在今天的小嘗試當中可以發現到，其實並不是每次單純的把資料丟進去處理就是 OK 的了，有些時候你必須要先對資料做一些預處理之後才能有好的效果，或甚至是才能夠順利運行。

起初我在寫這一份 code 的時候其實也是沒有做標準化的，中間會遇到 divide by zero in log 的問題，才會想到也許是因為數值過大，然後又搭配了 Sigmoid 函數，所以造成這樣的結果。

此外，這次也看到了另一種以 梯度 來視覺化結果的方法，雖然與預期的直線有所不同，但也讓我多認識到一個可以簡單視覺化 Logistic Regression 的小工具。

至此我們已經看過了幾個實作，但中間仍然有許多的問題尚未回答，而是單純地把資料丟進預想的模型當中，然後 Loss 跟模型看起來就都會還不錯了。

接下來我們會花一些時間去了解在實作的過程當中可能會遇到那些問題，而這些問題又應該要用怎樣的方式去處理比較妥當，或是普遍來說會怎樣實作。