[未完稿 qwq]

昨天我們談了 SVM 的基本概念，知道他是一個能夠做 Classification 的工具，並且比起 Logistic Regression，因為有了 Large Margin 的特性，使得它能夠有相當不錯的表現，而且能夠避免 Outlier。

今天我們要再談到 SVM 能夠劃出非線性的 boundary 這個特性。

Some Great Intuitives

過去我們解決 Classification 問題的時候考慮的通常都是一個單一的直線或是平面去切割出兩個區域，不過如果現在資料散佈的狀態無法單純使用一個直線去切開的話，這時候就會很需要有非線性的方法。

像是這一個例子，顯然任何一條直線都不太能夠直接切割出好的區域。

看似困難的問題，轉換視角也許能有不同啟發

如果我們試著把這些點投影到 3D 空間上，像是底下的圖片。
欸，是不是海闊天空！

透過這種投射到另一個維度，能夠讓我們有更加直覺的方法去找出一個平面切出兩個區域，這個區域就比較直覺了。

Kernel

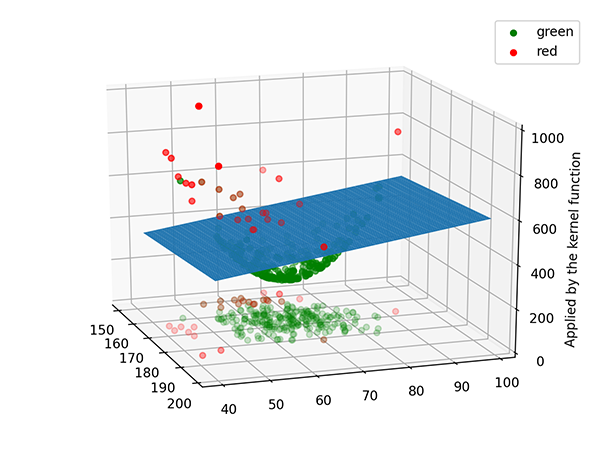
那麼要如何投影到更高的維度呢，並且能夠維持原先資料彼此之間的關係，不會使得投影過後切割出來的區域跟原先的資料並不相關呢？SVM 的作法是透過定義一個被稱為 Kernel 的東西。

Kernel 基本上只是一個內積函數，而並非直接將資料投影到一個更高維空間，而是單純的告訴你在這個高維的空間當中，點跟點之間的內積關係。Kernel function $K$ 必須要符合 Mercer's theorem 。

• $K$ 是對稱函數，意即 $K(x_i, x_j) = K(x_j, x_i)$
• $K$ 是連續函數
• $K$ 這個變換以矩陣來表示

最終我們的 Kernel Function 一定可以找到一個 $\phi(x)$ 使得

$$
K(x_i, x_j) = \phi(x_i)^T\phi(x_j)
$$

有了 Kernel Function 之後我們就可以把每個資料丟進去 Kernel Function

• Linear
  $$
  K(x_i, x_j) = x^Tx
  $$
• Polynomial
  $$
  K(x_i, x_j) =
  $$