延續昨天的，還有神經網路跟深度學習沒有寫
今天把這部份寫完。
昨天已經用線性模型做了一遍，那如果是用神經網路怎麼做呢?

再回看講師的nnnotebook

神經網路

首先什麼是神經網路? 這個網路上已經有很多相關知識
所以就不再贅述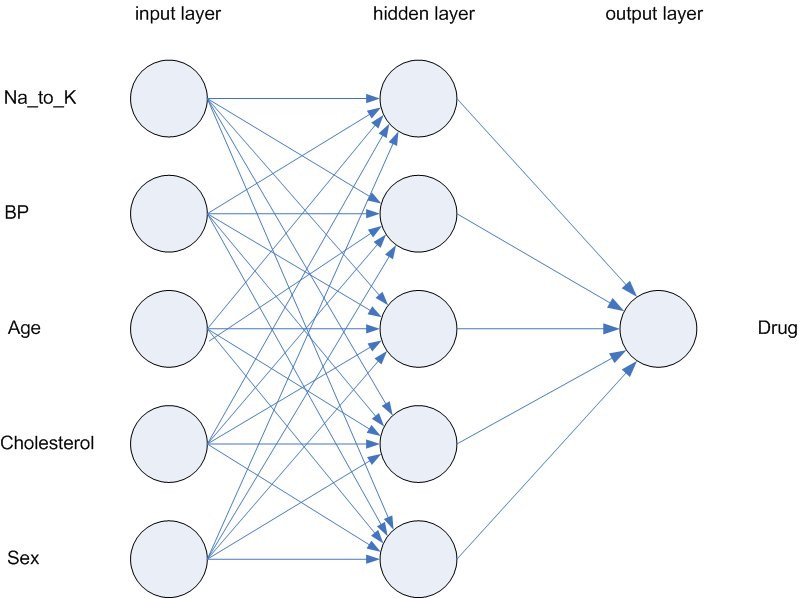

由上圖可知，很多個特徵被當成神經元，中間有一層hidden layer ，最後會有一個輸出層。
所以我們就來看一下講師怎麼帶我們寫code!

def init_coeffs(n_hidden=20):
    layer1 = (torch.rand(n_coeff, n_hidden)-0.5)/n_hidden
    layer2 = torch.rand(n_hidden, 1)-0.3
    const = torch.rand(1)[0]
    return layer1.requires_grad_(),layer2.requires_grad_(),const.requires_grad_()

init_coeffs這個function 顧名思義，就是初始化係數。
那function 裡面又做了什麼事呢?
可以看到有2層，第1層torch.rand(n_coeff, n_hidden) 創建了一個隨機矩陣 ，元素在0~1 之間，-0.5 跟之前的操作一樣，只是為了把範圍控制在[-0.5~0.5]

比較特別的是他特地除以hidden的層數(n_hidden)
我理解這主要是確保權重的範圍，避免梯度爆炸或是梯度消失的問題
第2層torch.rand(n_hidden,1)-0.3
torch.rand(n_hidden, 1)：這邊建立了一個形狀為 (n_hidden, 1) 的隨機張量。這個張量表示了第二個隱藏層的權重矩陣。n_hidden 代表隱藏層中的神經元數量，這裡的 1 表示輸出層只有一個神經元。
這個矩陣中的每個元素都是從均勻分佈（在0到1之間均勻分佈）中隨機抽樣的。

-0.3：初始化後，這個隨機矩陣的每個元素都會減去0.3。
這是為了對權重進行一些小的偏移或擾動。在神經網路中，這種偏移可以幫助打破對稱性，並且可以更快地訓練出不同的特徵檢測器。

const 就是用來初始化神經網路的常數項，也就是bias。這個bias將在神經網路的運算中會被加到輸入和權重的線性組合中，以調整網路的輸出。這樣可以增加網路的表達能力，這樣可以擬合不同的數據模式。

最後把這3個tensor 都加入梯度追蹤計算, 並且回傳。到此我們的初始設定就完成了

def calc_preds(coeffs, indeps):
    l1,l2,const = coeffs
    res = F.relu(indeps@l1)
    res = res@l2 + const
    return torch.sigmoid(res)

l1,l2,const 表示第1層的權重，第2層的權重，與常數項。
res = F.relu(indeps@l1) 這邊是神經網路的第一層運算，
先將indeps 與 l1 做矩陣相乘（indeps@l1）然後通過 F.relu 函數應用非線性激活函數 ReLU（修正線性單元）到矩陣乘積的每個元素上

關於relu可以參考解釋

res = res@l2 + const
接下來，將中間結果 res 與第二層權重 l2 做矩陣相乘（res@l2），並將常數項 const 加到結果上。

`return torch.sigmoid(res)：最後，將第二層的輸出 res 通過 sigmoid 函數進行轉換，以計算最終的預測值。sigmoid 函數將輸出的值映射到範圍 [0, 1]，用於表示二元分類的概率。

寫好了初始化權重，也寫好了預測，接下來我們就要寫update 權重
不斷的優化update 之後，才能選一個較好的pred

def update_coeffs(coeffs, lr):
    for layer in coeffs:
        layer.sub_(layer.grad * lr)
        layer.grad.zero_()

這邊主要目的是根據梯度下降法來調整模型的權重，以降低損失函數的值
程式相當簡單
他把遍歷每一層權重，針對每一層，都做.sub_(), 將梯度存在layer.grad中
再乘上lr 後剪去，這樣就可以更新權重
最後再用grad.zero_() 的方法將權重的梯度清零，以準備下一輪梯度計算。

所以我們這邊就是重寫了這幾個方法，再重用前一天的train_model 來跑跑看!

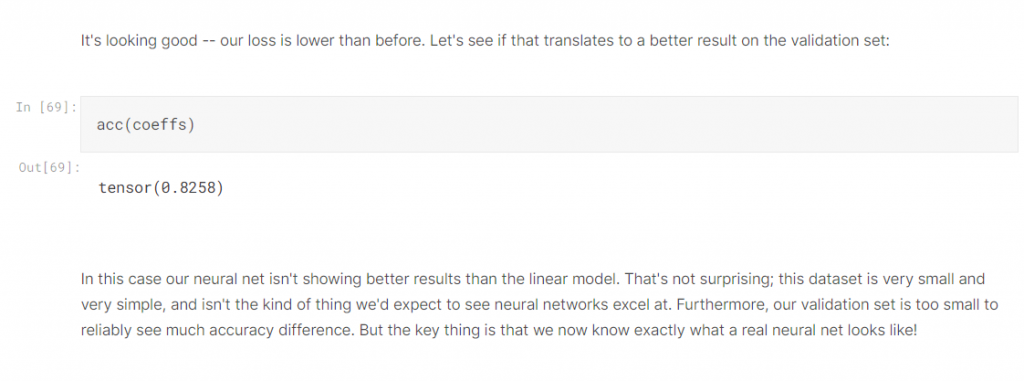
結果並沒有比較好! 反而更差了!這也就說明了為什麼以前神經網路沒人用
後面發展出深度學習才大紅大紫。

但講師的這段程式太簡潔了，看了很久，今天就先這樣