昨天介紹兩個常用的損失函數，今天要帶大家認識：如何最小化損失函數的值？
我們可以用 「梯度下降法」 或是 「反向傳播」 這兩個方法調整機器學習模型的權重和參數讓誤差極小化。今天先跟大家介紹「梯度下降法」明天來介紹反向傳播

梯度下降法（Gradient Descent）

梯度下降法（Gradient Descent）是通過計算損失函數對於模型參數的梯度（斜率），來指示在當前權重和參數下，如何調整它們以減小損失。我們來舉兩個簡單好懂的例子

梯度下降法的主要思想是根據損失函數的梯度信息來找到損失最小化的方向，並向該方向調整參數。這樣的過程反覆進行，直到達到收斂，模型參數不再有顯著的變化。不同變種的梯度下降法，如批量梯度下降、隨機梯度下降和小批量梯度下降，區別在於每次計算梯度時使用的數據樣本數量。

梯度下降法在機器學習和深度學習中廣泛應用，用於訓練各種類型的模型，包括線性回歸、神經網絡、支持向量機等，以優化模型的性能。

1.想像你是一位地質學家，你站在山頂，這次的目標是尋找山上的「最低點」（即損失函數的最小值）。雖然你站在山最高處，但你不知道哪個方向才是最陡峭下降的方向。所以梯度下降法則告訴你幾個方法：

• 觀察地勢：首先觀察自己所處的位置的坡度和傾斜方向，這相當於計算損失函數對當前參數的梯度。

• 向下走一步：根據你觀察到的坡度和傾斜方向，選擇一個合適的方向，並向下走一步，然後重新觀察地勢。

• 反覆迭代：你一直反覆執行觀察地勢和向下走的步驟。

• 找到最低點：當你不再能夠走下去，你會停下來，這時你所處的位置就是山腳的最低點，也就是損失函數的最小值。

2.想像我們現在在人生顛峰，因為太累了所以現在要換一份最輕鬆的工作。我們不知道哪個工作是最輕鬆的，所以需要在不斷嘗試的過程中找到最適合的。所以梯度下降法則告訴你幾個方法：

• 觀察：觀察市場的需求，這相當於計算損失函數對當前參數的梯度。

• 目標函數：找到最輕鬆的工作，這就是我們的目標函數，我們要使得這個理想度最大化。

• 嘗試工作：開始尋找工作，不斷地應聘不同的職位。每份工作應聘都相當於一次迭代，試圖找到一份輕鬆度更高的工作。

• 反覆迭代：根據每份工作的理評估，逐漸調整自己的求職策略。如果一份工作的輕鬆度高於當前工作，就會考慮接受這份工作。（梯度下降法不斷調整模型參數以尋找最小的損失值。）

• 找到最佳工作：當無法找到一份比當前工作輕鬆的工作，或者達到了某個停止條件，就會決定接受目前的工作，認為它是最好選擇。

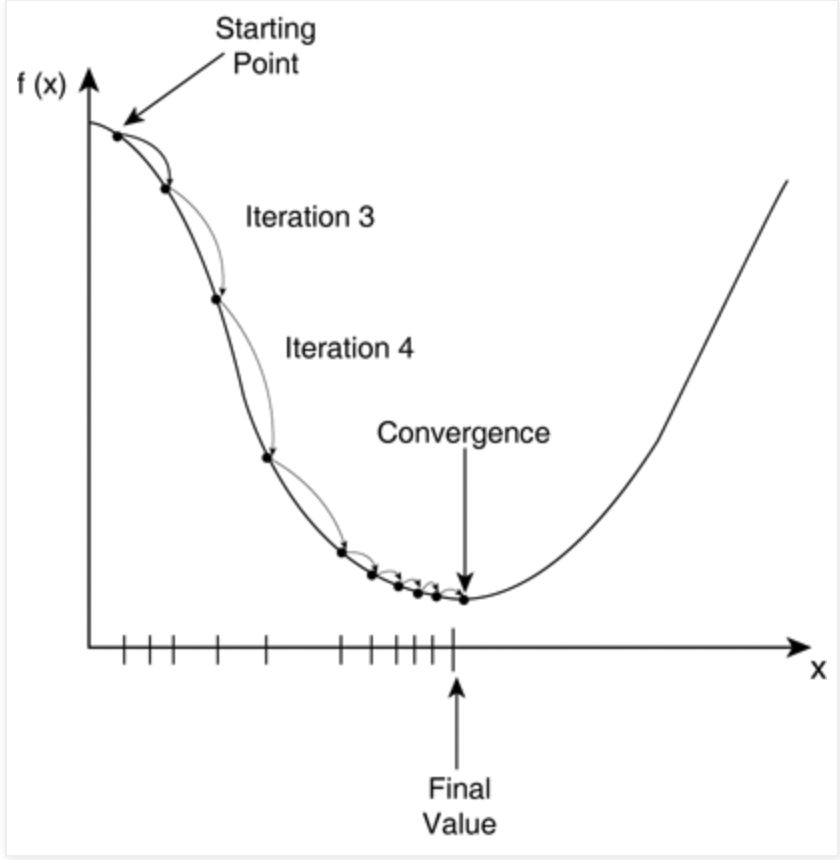
資料來源：http://strivingworksmartobserver.blogspot.com/2017/05/ml-stochastic-gradient-descent.html 搜尋日期：2023/09/26
X是為權重，y則為損失值，希望損失值減少（往谷底走）

當然我們在架設模型時，不太可能只有一個參數，就像我們之前寫出來的神經網路模型總共有50890個參數。無論模型有多少個可訓練參數，利用梯度下降法反覆迭代修正權重參數，使權重參數值調整到損失值得最低點就是我們在追求的。