由前文中貝氏定理的敘述，觀察先驗的假設為離散的狀況: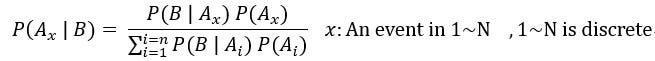

其分母會是一個固定的常數。所以後驗機率會與分子有正相關，也就是和"概似度乘上先驗機率"有正相關: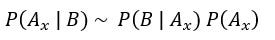

觀察貝氏定理，如果先驗的假設為連續的狀況: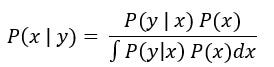

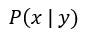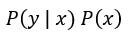其分母是固定的，可視為常數，所以是與分子有正相關， 也就是和"概似度乘上先驗機率"有正相關: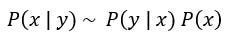

對於連續的假設，有無限的值，需要用到機率密度函數（Probability density function，簡寫作PDF ）之分佈來假設先驗機率。

機率密度函數有這些定義的分佈:

The probability density function including Standard normal distribution, beta distribution, gamma distribution, exponential distribution, Weibull distribution, Cauchy distribution, Log-normal distribution etc…

面對這些函式，如果對於貝氏定理中的分母，要對這些PDF函式積分，有時非常困難程式化；如果有共軛之證明推導出的公式，會相對容易計算出後驗分佈，如果沒有則令人頭痛。另一方面，我們可能無法得知一開始的先驗分佈最好的參數，只能用平均或建議的值來做起始。

馬可夫鏈蒙地卡羅MCMC中有一種方法可以避開複雜的積分運算，面對各種建議分佈，此演算法為: Metropolis–Hastings。

假設以貝氏定理的公式: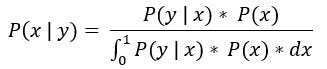

其步驟為:

Step1:
先選出一個初始假設後驗

Step2:
以適當的機率密度函數，當作先驗分佈(本輪的先驗分佈)。

Step3:
因為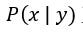正相關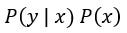，所以於先驗分佈中，求出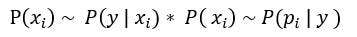

Step4:
由Step2的先驗分佈中，以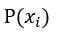當作新的建議分佈的平均中點，然後計算此建議分佈的參數，新的建議分佈就產生了。

由算出的新的建議分佈中，隨機找出一個假設當作建議假設，為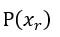， r 表示隨機的意思，建議假設也取得了。

Step5:
因為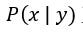正相關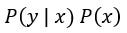，所以於Step2中的分佈(本輪的先驗分佈)，求出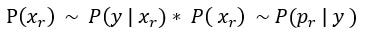

Step6: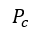
是初始假設算出來的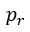，是建議假設算出來的，都是以Step2中的分佈(本輪的先驗分佈)來計算。於此步驟要選出一個當作下一輪迭代的候選初始假設(相當於Step1)。

選擇方式為: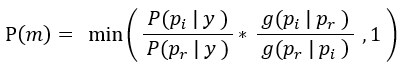

而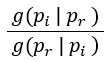為轉換因子，也可看成修正參數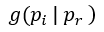，表示初始假設先驗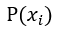再以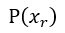為中心的建議分佈的機率密度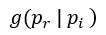，表示初始假設先驗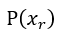，再以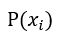為中心的建議分佈的機率密度。

Step7:
如果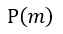等於1，則保留;
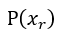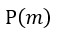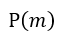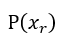如果小於1，則從 0~1均勻分佈中隨機抽一個數字，若小於則保留，反之保留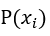

Step8:
重新至Step1，將初始假設後驗改為Step7所選擇。

經過多輪的迭代，將每個Step7的次數統計成百分比(每種假設所出現次數 / 總共幾輪)，會形成一個統計出來的後驗分佈，也就是我們所要求出的後驗分佈。

參考資料:

https://vioshyvo.github.io/Bayesian_inference/conjugate-distributions.html

https://jvanderw.une.edu.au/L10_IntroBayesianInferenceandConjugateModels.pdf

貝氏統計：原理與應用 , 邱皓政 , 2020

https://en.wikipedia.org/wiki/Metropolis%E2%80%93Hastings_algorithm

https://bookdown.org/rdpeng/advstatcomp/metropolis-hastings.html

https://bookdown.org/rdpeng/advstatcomp/metropolis-hastings.html

https://towardsdatascience.com/a-zero-math-introduction-to-markov-chain-monte-carlo-methods-dcba889e0c50

AI 必須！從做中學貝氏統計 , Therese M. Donovan, Ruth M. Mickey , 2022

http://www.columbia.edu/~mh2078/MachineLearningORFE/MCMC_Bayes.pdf

https://en.wikipedia.org/wiki/Monte_Carlo_method

https://statweb.stanford.edu/~cgates/PERSI/papers/metrop.pdf

https://people.duke.edu/~ccc14/sta-663/MCMC.html