此篇要來看貝葉斯定理如何去協助機器學習判斷的一些重點。前面文章有稍微提到貝葉斯也是透過不斷更新權重來達成最佳結果，於此來重點式了解其運作。

1.貝葉斯定理 Basic deduction of Bayesian theorem

推導的定理整理如下:

2.後驗機率由先驗機率更新的學習過程

圖解: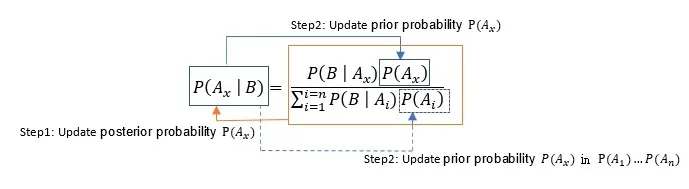

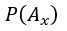為先驗機率，某個假設 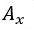成立的初始信心程度。
先驗機率相當於觀察資料以前，假設成真的機率；先驗有屬於自己的分佈(機率質量函數或機率密度函數)。邊際機率也可以描述它。

如果是離散的狀況，先驗分佈的總和必須為1；如果是連續的狀況，可解釋先驗分佈下的總面積要為1(積分為1)

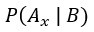為後驗機率，表示B假設成立時，某個假設 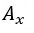亦成立的信心程度。

後驗機率也有自己的分佈(機率質量函數或機率密度函數，通常與先驗同樣性質，繼承先驗的分佈)，如果是離散的狀況，後驗分佈的總和必須為1；如果是連續的狀況，可解釋後驗分佈下的總面積要為1(積分為1)。

所以透過貝氏定理得到的後驗機率，其後驗分佈相當把先驗分佈做權重的分配後，所得到的新的分佈。權重可以依據概似度來決定。

上圖step1 為本次迭代時將計算的後驗機率更新後，step2再將每個更新後的後驗機率轉變成下一個迭代的先驗機率，重複多次迭代後，先驗機率分佈會趨近為一個收斂的分佈。

何謂概似度?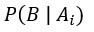
位於分母，為概似度，為觀察資料所得到的，表示在第i個假設成立時觀察資料B的機率；
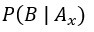位於分子，亦為概似度，為觀察資料所得到的，也是分母 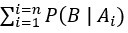的其中一個。概似度可以解釋成觀察已發生的資料形成的機率。概似度可以有各種數學分佈描述，再透過觀察資料計算。

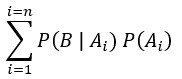表示概似度乘上先驗機率的總和，此總和不必為1，但一定是常數(固定)。

概似度可使用數學函式來描述，如機率質量函數或機率密度函數。透過觀察資料，利用數學函式所算出的概似度總和不必為1，因為概似度可由不同種的機率或參數算出來的。而機率質量函數或機率密度函數各自自己的分佈特性就是分佈中的和為1，所以算出的後驗機率分佈性質也同等為各自導入的機率質量函數或機率密度函數的性質，概似度只是過程，類似權重，有不同因子決定，所以其和不一定也不必為1。

補充說明

機率質量函數（probability mass function，pmf）

機率質量函數 是離散隨機變數在各特定取值上的機率。
數學描述為: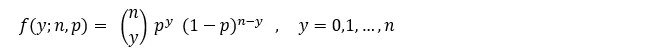

函數分佈中的所有值必須非負，且總和為1。

機率質量函數可以定義在任何離散隨機變數上，包括常數分佈, 二項分佈（包括伯努利(Bernoulli)分佈）, 負二項分佈, 卜瓦松(Poisson)分佈, 幾何分布以及超幾何分佈於隨機變數上.

機率密度函數（Probability density function，PDF ）

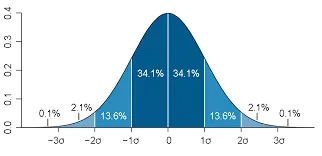
連續型隨機變數的 機率密度函數，在不致於混淆時可簡稱為密度函數，是一個描述這個隨機變數的輸出值，在某個確定的取值點附近的可能性的函數。圖中，橫軸為隨機變數的取值，縱軸為機率密度函數的值，而隨機變數的取值落在某個區域內的機率為機率密度函數在這個區域上的積分。當機率密度函數存在的時候，累積分布函數是機率密度函數的積分。

所有機率密度函數分佈中曲線下的面積為1。