今日學習重點

先前有些重要的知識我們尚未完全補充，因此我在今天我將會把這些部分都告訴你，讓你知道我們為何選擇使用此種損失函數與激勵函數，同時也會實作我一直未提及的中文斷詞方式，今天的主要內容包括以下幾點：

1. 隱藏式馬可夫模型(HMM)斷詞方式
2. 損失函數的應用場景與解析
3. 激勵函數解析與可視化

隱藏式馬可夫模型(HMM)

在中文斷詞的處理上，存在許多不同的方法，其中最基本的方式就是使用預先建立的詞彙字典來匹配文本中的詞語，這種策略稱為字典匹配法(Dictionary Matching Method)，但然而這種方法在處理廣大的中文字時，可能會遇到因異體字而導致該詞彙不在字典中的問題，或者遇到過多的生僻字等相關問題。

不過在中文的文法中，有些任務可能需要包含這些生僻字，因此許多方法傾向於採用統計學的做法，其中最常見的一種方法就是隱藏式馬可夫模型(HMM)。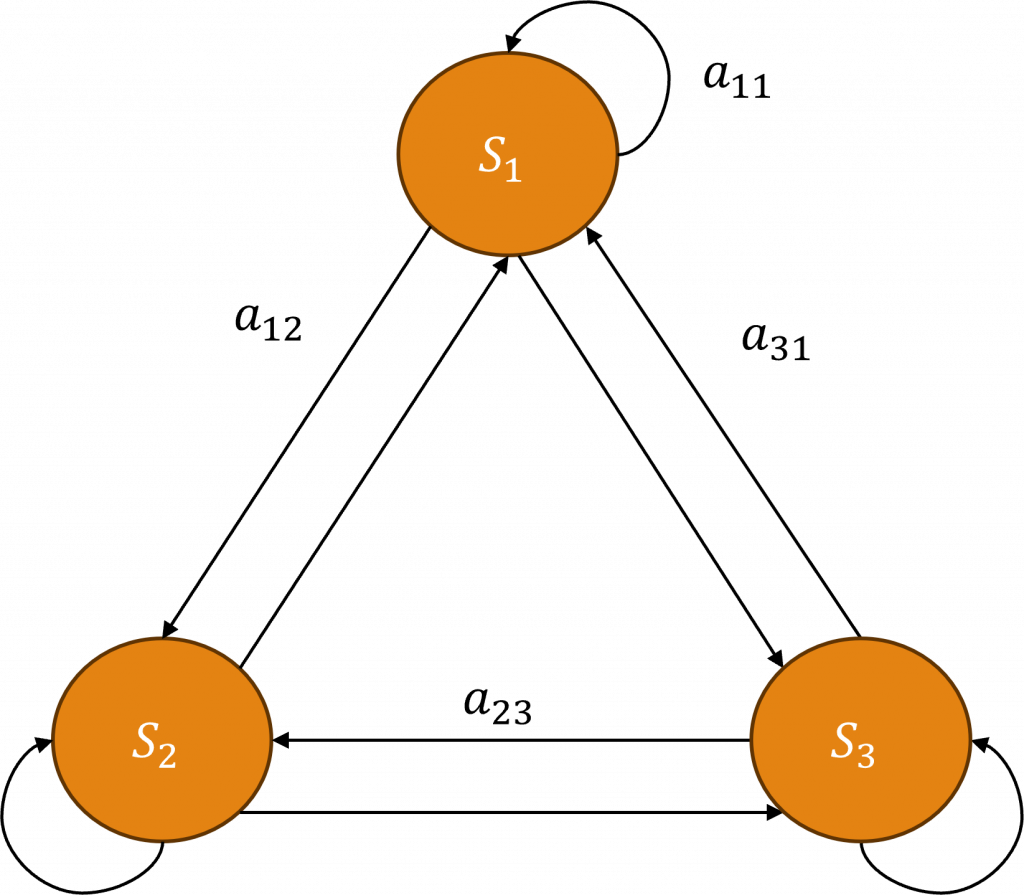

在隱藏式馬可夫模型中，我們將每一個文字稱之為S，並將連接兩個文字序列的稱為a，當進行文字處理時，該模型會發放出三個邊，其中包括自我連接a11、與下一個序列的連接a12以及與上一個序列的連接a13，這三個邊的總和將會等於1。

在演算的方式上，我們會隨機選擇一個狀態作為起點S0~Sn，然後按照設定的邊a進行移動，直到達到預先設定的最大步數，這樣我們便可以計算每一條路徑的機率值，擁有這個機率值後，我們能設定一個閾值，用來將可能文字路徑儲存下來。

雖然理論看起來相當簡單，可是實際上程式碼的應用稍微複雜一些，畢竟該演算法主要工作內容是計算出所有的路徑，並針對所有序列的概率進行估算，以從中找出最有可能的文字解析，因此還會衍生出更多的演算法，但這可能跟深度學習關聯性不大，在這裡我們只需瞭解該演算法的基本原理即可。

在實現程式碼的部分，Python中有個名為Jieba的中文斷詞函式庫，其可以幫助我們進行這些複雜的計算。在以下的程式中你將會看到，只需執行該段程式碼，就能輕鬆地完成斷詞工作。

# 需先執行pip install jieba

import jieba
text = "我喜歡自然語言處理"
seg_list = jieba.cut(text, HMM=True)
print("/".join(seg_list))
#---------------輸出------------
我/喜歡/自然/語言/處理

損失函數

我們在訓練模型時，使用了多種不同的損失函數來進行訓練，但對於剛開始學習這些知識的你，可能對於其用法並不十分理解，因此當時我並未深度講解，而現在我決定將我們使用過的所有損失函數進行整理並解析，並指出在哪些情況下需要使用這些損失函數。

二值交叉熵损失(Binary Cross-Entropy Loss, BCEloss)

二值交叉熵損失（Binary Cross-Entropy Loss)是一種針對二分類問題的損失函數，該函數主要對模型在二分類任務中的最後輸出結果進行評估，其計算方式如下：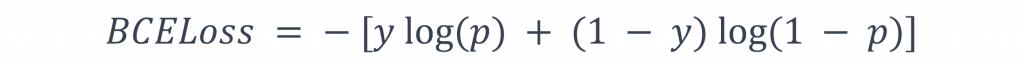

在計算公式中，y是我們賦予模型的標籤，它通常是0或1，而p則是模型最終的輸出結果，常常會使用sigmoid函數來將其縮放至0~1的範圍內。當y等於1時，我們希望「(p)越接近1越好」，這對映的是公式ylog(p);當y等於0時，我們則希望「(p)越接近0越好」，這對映的是公式(1 - y)log(1 - p)。透過這樣的調整方式，使p的數值能越來越接近實際的標籤數值。

交叉熵損失（CrossEntropyLoss）

交叉熵損失（CrossEntropyLoss）主要適用於分類任務，包含二分類與多分類，它常見於多類別分類任務中，交叉熵損失的基本概念是去評估模型預測輸出和標籤之間的差距，對於一個使用One-hot encoding編碼的樣本，交叉熵損失的計算是如下進行的：

此公式中我們進行了不同的類別機率的對比，通過p(i)以及log(p(i))的相乘，我們可以嚴懲預測機率和標籤1之間的差異，同時也對其他類別的預測機率與0之間進行處置，如果模型的預測趨近於真實標籤。

在Pytorch中，該公式已經內含了softmax與One-hot encoding的運算，因此針對我們的模型輸出，就不應該再進行softmax處理，以免產生計算上的錯誤。

NLLLoss (Negative Log Likelihood Loss)

NLLLoss (Negative Log Likelihood Loss)與交叉熵損失都專門用於多類別分類任務且十分相似。不過NLLLoss的公式不需要進行One-hot encoding的轉換，所以在運算速度上會較快。

因此在處理輸出量大的情況時，我們通常會使用NLLLoss，該方法的計算原理非常直觀，它透過-log來衡量預測值與實際值之間的差距，透過這樣的方法，可以使數值更穩定，下列是它的計算公式: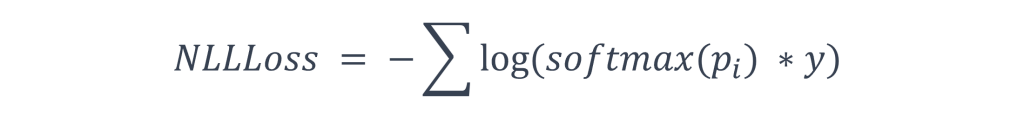

小提示:
-log是一種常用的方法，用來簡化機率分佈的變異數，當我們選擇使用對數概似函數作為損失函數，它可輕易的與其他損失函數進行對比及組合，以滿足不同問題的需求，因此在損失函數中常常會看到-log的身影。

激勵函數

我們先前已經介紹過許多激勵函數，所以你應該對此有基礎的認識了，而現在我將進一步地將這些函數可視化，並解釋它們的使用場合，但在開始之前我們需要先定義一個函數，讓我們能接收外部輸入的激勵函數公事以及x軸範圍為參數，以便進行可視化的動作。

def draw(x, label, activation):
    # 標題
    plt.title(f'{label} Function')
    # X Y軸名稱
    plt.xlabel('Input')
    plt.ylabel('Output')
    
    # 圖表大小
    plt.figure(figsize=(8, 6))
    
    # 繪製折線圖
    plt.plot(x, activation(x), label=label, color='b')
    
    # 格線樣式
    plt.axhline(0, color='black',linewidth=0.5)
    plt.axvline(0, color='black',linewidth=0.5)
    # 顯示格線
    plt.grid(True)
    plt.legend()
    plt.show()

ReLU

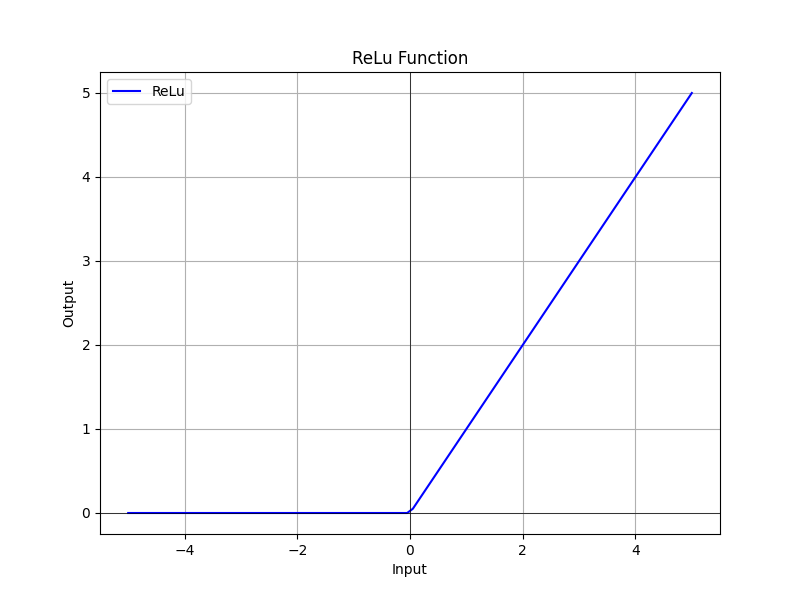
ReLU函數的主要功能在於協助神經網路學習非線性關係，在處理複雜數據和任務時，這維度的重要性不言而喻，這原因可以歸結為Wx+b的最終計算結果均為線性，因此使用該函數能更破壞掉這種線性關係，使其更有效地產出接近實際狀態的輸出，讓我們一起看下方的公式：

該公式代表著，當輸x大於零時ReLU函數傳回x本身，當x小於或等於0時ReLU返回0，這同時也代表著該神經元並不會被啟用，這種方式有助於神經網路進行強化特徵和剔除特徵的功能，該曲線我們可以透過以下程式來生成:

def relu(x):
    return np.maximum(0, x)
    
x = np.linspace(-5, 5, 100)
draw(x, 'ReLu', relu)

但這種方式也存在一些問題，當輸入為負數時，輸出平均值為零，於是會產生所謂的死亡神經元問題(Dead ReLU Problem)，也就是某些神經元可能永遠無法被激活，不過ReLU的效能仍然十分強大，因此仍然是神經網路中最常用的激活函數之一。

Softmax

softmax的作用主要是將一組原始分數z(i)轉換成表示機率分佈，該函數能夠將每個z(i)轉換為介於0到1之間的機率值，並同時確保所有類別的機率總和等於1。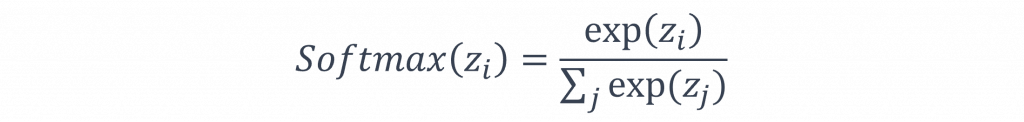

該公式我們有在【Day 10】掌握文字翻譯的技術(中)-為何需要注意力機制中，曾經簡單提及過注意力分數的計算方式，其實現方式如下。

def softmax(x):
    e_x = np.exp(x - np.max(x))  
    return e_x / e_x.sum()
    
x = np.linspace(-5, 5, 100)
draw(x, 'Softmax', softmax)

tanh

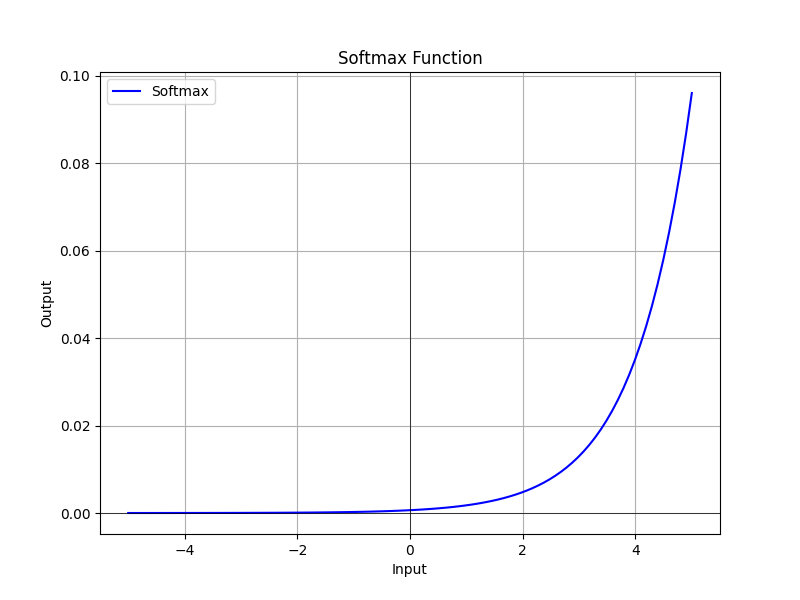
tanh函數的輸出範圍在-1~1之間，這表示對於任何實數輸入，輸出都會在這個範圍內，並且該函數輸出均值為0。這意味著當輸入接近0時，tanh的輸出接近0，所以它包含正負值的資料更具區分性(中心化性質)，所以該函數常見於時間序列模型中，作為計算資料機率分布的狀態，該曲線的公式如下。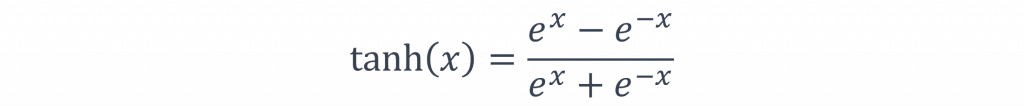

它通常被應用在神經網路的隱藏層，因中心化性質與S曲線的特色使其能夠處理各種資料分佈，進而解決一些梯度消失的問題，在許多情況下它被認為是sigmoid函數的替代選擇，以下是該曲線的實現方式：

def tanh(x):
    return np.tanh(x)
    
x = np.linspace(-5, 5, 100)
draw(x, 'tanh', tanh)

sigmoid

Sigmoid函數的輸出範圍介於0~1之間，這對於處理二元分類問題極為實用，因為我們可以將該輸出直接作為機率值，同時Sigmoid是一種平滑曲線函數，意味著它在整個輸入範圍內都可以連續求導，此特性對於梯度下降等最佳化演算法的運作非常重要，其數學函數公式如下：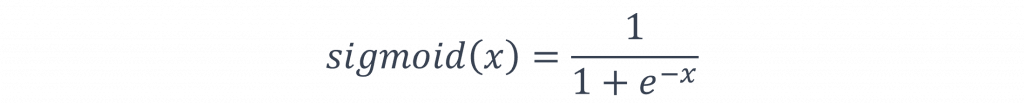

Sigmoid也有一些缺點，其中一個主要問題是當輸入遠離零時，梯度會接近於零，這與ReLU所造成的問題相同，因此他也會產生梯度消失問題，其實現曲線的方式如下:

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
    
x = np.linspace(-5, 5, 100)
draw(x, 'Sigmoid', sigmoid)

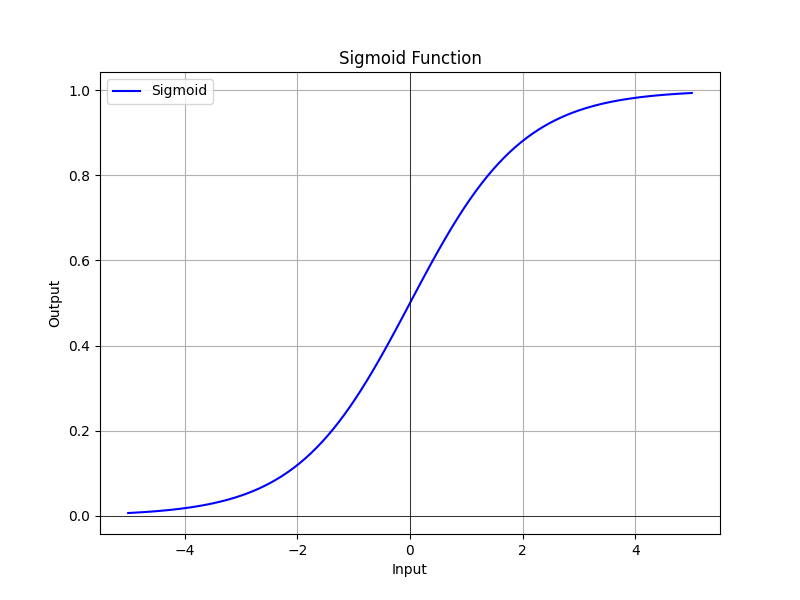
從以上的激勵函數中，我們可以瞭解到雖然不同的激勵函數對應的動作各有所異，並也都存在各自的優缺點，因此在設計神經網路時，我們必須考慮這些函數的特性，並進行實驗以決定什麼樣的設計最合理才是最正常的模型設計方式。

後話

這次我將介紹了一些在深度學習中至關重要但之前未提及的概念和技術，深入理解這些內容對於掌握神經網路的調整與訓練過程十分關鍵，如果你已經掌握了我們到目前為止所學習的內容，那麼對於當下市面上的自然語言處理模型，你應有一定程度的認識，不過你還需要進一步強化模型訓練策略，所以我將會陸續介紹一些在自然語言處理領域中，市場上的經典模型。

那麼我們明天再見！

內容中的程式碼都能從我的GitHub上取得:
https://github.com/AUSTIN2526/iThome2023-learn-NLP-in-30-days