【Day 16】解析詞嵌入預訓練模型的奧秘(下)-fastText中Subword建立的重要性

2023 iThome 鐵人賽

DAY 16

AI & Data

30天內成為NLP大師：掌握關鍵工具和技巧系列第 16 篇

15th鐵人賽

austin70915

2023-10-01 21:13:03

386 瀏覽

分享至

前言

今天我們將結束對詞嵌入預訓練模型理論的討論，在前面的幾天中你可能會發現範例程式碼中，有些部分和公式有所出入，這是因為這些詞嵌入預訓練模型原本並非「深度學習」模型，而是屬於「機器學習」的範疇，並且最一開始是採用非監督式學習(Unsupervised Learning)來進行任務，也就是在無標籤的情況下進行學習。不過這些技術已被廣泛運用於「深度學習」的詞嵌入層中，因此我採取了一些方法將其轉換成深度學習模型。

那為何要這樣做呢？因為我們可以運用這些已經被訓練過的詞嵌入預訓練模型，並通過時間序列模型來更全面地調整這些文字的權重。而今天我們將會學習這些詞嵌入預訓練模型的最後一項重要技術fastText，今天的學習重點如下:

理解子詞（Subword）的建立方式
理解子詞（Subword）的向量合併方法
學習層次Softmax（Hierarchical Softmax）的原理

fastText

相較於我們前幾天所講解的兩種詞嵌入預訓練模型，FastText的效能表現出類拔萃，它是基於Word2Vec中的CBOW方法進行變化的方法，使其不僅考慮每個字的上下文訊息，還能分析詞彙內部的子詞（Subword）訊息，因為這樣的設計FastText能夠理解並處理詞彙中的詞綴，對於處理稀有詞彙或罕見詞彙也有極其出色的表現，所以這項技術非常適合處理特定領域的文本或高度專業化的任務，而它的主要技術特點包括了子詞嵌入（Subword Embeddings）和層次Softmax（Hierarchical Softmax）。

子詞嵌入（Subword Embeddings）

在Word2Vec與GloVe的模型中，我們都是透過滑動一個視窗來找尋文字的前後詞彙，這種動作的專有名詞叫做N-Gram，它這是語言模型的一種演算法，其基本概念是按照文字內容的位元組順序進行大小為N的滑動視窗操作，最終生成長度為N的位元組片段序列。

而在模型fastText中就會先對每一個詞彙進行N-gram的切割，然後將其放入到詞嵌入向量空間中，我們可以先看到以下的簡易程式碼:

def create_subwords(word, min_length=3):
    subwords = []
    length = len(word)
    
    for start in range(length):
        for end in range(start + min_length, length + 1):
            subword = word[start:end]
            subwords.append(subword)
    subwords[0] = "<" + subwords[0]
    subwords[-1]= subwords[-1]+ ">" 
    
    return subwords

word = "apple"
subwords = create_subwords(word)
print(subwords)
#----------------輸出----------------
['<app', 'appl', 'apple', 'ppl', 'pple', 'ple>']

在上述的程式碼中，我們可以看到<代表文字的開頭，而>代表文字的結尾，而在fastText模型中apple這個詞彙的向量表達就是這六個詞彙向量的整合（我們可以透過torch.mean來整合向量訊息），當然在實際模型運作中，詞彙的切割方式可能會更加繁複，這裡我們只是提供一個簡化的範例程式。

層次Softmax（Hierarchical Softmax）

我們先前所使用的Softmax需要透過不斷的迭代計算出每一個結果的機率，導致在計算效率上極度緩慢，其時間複雜度達到O(N)，然而在fastText中，它選擇使用層次Softmax（Hierarchical Softmax）的方式來將時間複雜度降至O(logN)，而能讓它降低複雜度的方法就是透過霍夫曼樹（Huffman Tree）來找出每個解的最短路徑，現在讓我們來看看這種方式的具體操作。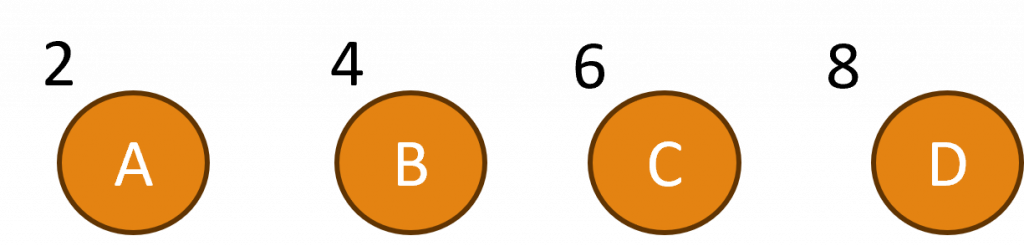

假設我們有一個向量z，包含四個類別(葉節點)N，而每一個類別都有其對應的權重資訊。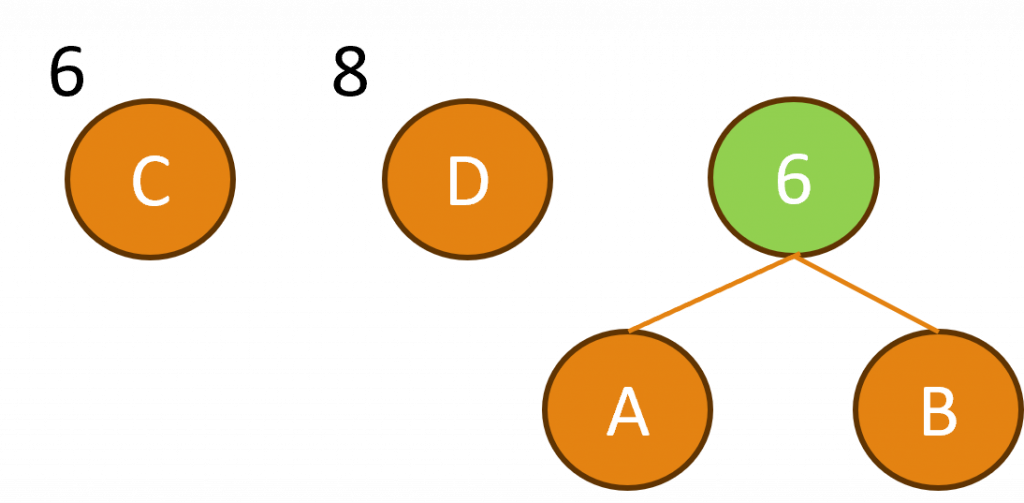

接下來我們將運用霍夫曼樹來建立一個二元樹結構，在此過程中會將兩個最小的葉節點N合併成一個新的內部節點，而這個新節點的權重將等於原先兩個葉節點的權重相加。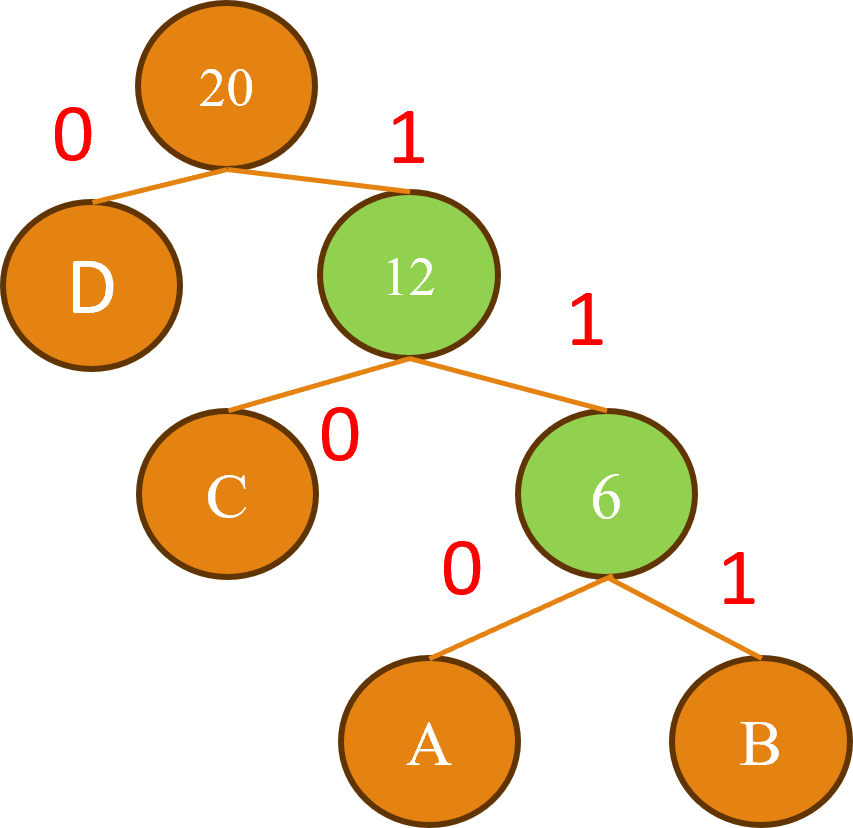

接下來不斷的重複這個合併的過程直到所有節點都被合併完畢，當樹建立完畢後我們將右節點編號作為1，左節點編號作為0，藉此建立了一個霍夫曼樹的結構。

而我們對於層次Softmax需要計算從根節點到每個葉節點的路徑機率，當計算到達葉節點的機率時，就代表得出了一個特定的類別，我們可以使用以下公式來進行計算：

在這個公式中我們首先將向量z與每個內部節點的權重W(i)進行內積運算，然後將結果通過Sigmoid函數σ，來將其轉換為範圍在0~1之間的機率值，根據這個機率值，我們便可以決定是選擇左子節點或是右子節點，而我們會持續這樣的操作，直到到達葉節點為止，最終則會輸出該葉節點所對應的類別機率。

這也就是層次Softmax的運作原理，簡單來說它就是透過利用霍夫曼樹的結構，來降低計算時間的複雜度，以簡化多類別分類的計算過程，以下是該方法程式碼實作的實際結果：

class HierarchicalSoftmax(nn.Module):
    def __init__(self, input_size, num_classes):
        super(HierarchicalSoftmax, self).__init__()
        self.num_classes = num_classes
        self.tree = self.build_tree(input_size)

    def build_tree(self, input_size):
        tree = nn.ModuleList()
        for i in range(self.num_classes):
            tree.append(nn.Sequential(
                nn.Linear(input_size, 1),  
                nn.Sigmoid(),
            ))
        return tree

    def forward(self, x):
        outputs = []
        for i in range(self.num_classes):
            output = self.tree[i](x)
            outputs.append(output)
        return torch.cat(outputs, dim=1)

在上述程式碼中，因建立一個葉節點需要知道模型的輸出大小，但我們不確定模型的輸出大小，因此我們可以使用ModuleList()來動態建立葉節點，而整體計算過程相單簡單，我們只需分別針對各類別使用不同的σ(W(i)z+b)進行計算，並將計算結果存入outputs串列中，最後將這些串列結合，就能代表每個葉節點的機率。

後話

你是否發現FastText的算法看起來比其他兩種更簡單一些呢？這是因為FastText的出現時間要晚於Word2Vec和GloVe，（分別是在2016年、2013年及2014年），較晚的發展給FastText帶來了一個優勢，就是可以直接以深度學習的角度來進行計算，因此與基於機器學習的Word2Vec和GloVe相比它的算法公式更為精簡，如果你想深入瞭解如何簡化Word2Vec和GloVe的公式，你可以參考我過去寫的程式碼，那裡有詳細地實現了用深度學習方法簡化複雜機器學習公式的過程，明天我將正式比較這三種模型的效能差異。

那麼我們明天再見！

內容中的程式碼都能從我的GitHub上取得:
https://github.com/AUSTIN2526/iThome2023-learn-NLP-in-30-days