圖片來源

今天開始要來講演算法相關的主題，在進入「最大數與最小數找法」之前，要先來談談 Big O Notation

▌Big O Notation (大O表示法)

Big O notation, sometimes also called “asymptotic analysis”, primarily looks at how many operations a sorting algorithm takes to completely sort a very large collection of data

如同以 KPI 作為一個工作績效的衡量指標，衡量演算法效益的指標就是 Big O Notation， O 代表 "Order of"（次序）的 function，表示演算法的時間複雜度（執行速度），以運算次數來計算執行速度

例如：今天 TODO List 裡有 n 筆資料，簡易搜尋法會需要執行 n 次，執行時間是 O(n)。二元搜尋法 會需要log n 的步驟來執行這 n 筆資料，執行時間是 O(log n)
n：正整數，代表輸入規模、資料量大小，可簡單看為要排序的陣列長度

常見的Big O 執行時間，「由快到慢」排列：

• O(1)：無論輸入的大小如何增加，執行時間都保持恆定，不隨著輸入大小的變化而變化
• O(log n)：也稱為對數時間，是一種時間複雜度，代表演算法有「二元搜尋法」
• O(n)：也稱為線性時間，代表演算法有「簡易搜尋法」
• O(n * log n)：執行時間隨著輸入大小n的增加而呈線性對數增長。代表演算法有「快速排序法」
• O(n ^ 2)：執行時間與輸入大小的平方成正比，代表演算法有「氣泡排序法」、「插入排序法」、「選擇排序法」
• O(n!)：又稱「階層」時間，非常慢的演算法

PS. 在演算法中，log n 通常指的是以 2 為底的對數，即以二進制為基數的對數。例如：log 8 = 3

▌逐一比較法

從第一個數看起，記錄到目前為止最大或最小的數，逐一往後面的數找下去，如果接下來的數比所記錄的數更大或更小，就取代之，直到最後一個數為止

舉例：請找出 8、56、49、38、7、64、25、76 裡「最大數」、「最小數」

▪「最大數」

• 步驟一：找出目前最大的數：8
• 步驟二：56 比 8 還大，所以 56 變成目前最大數，以此類推，一個一個比下去
• 步驟三：得到的最大數為 76

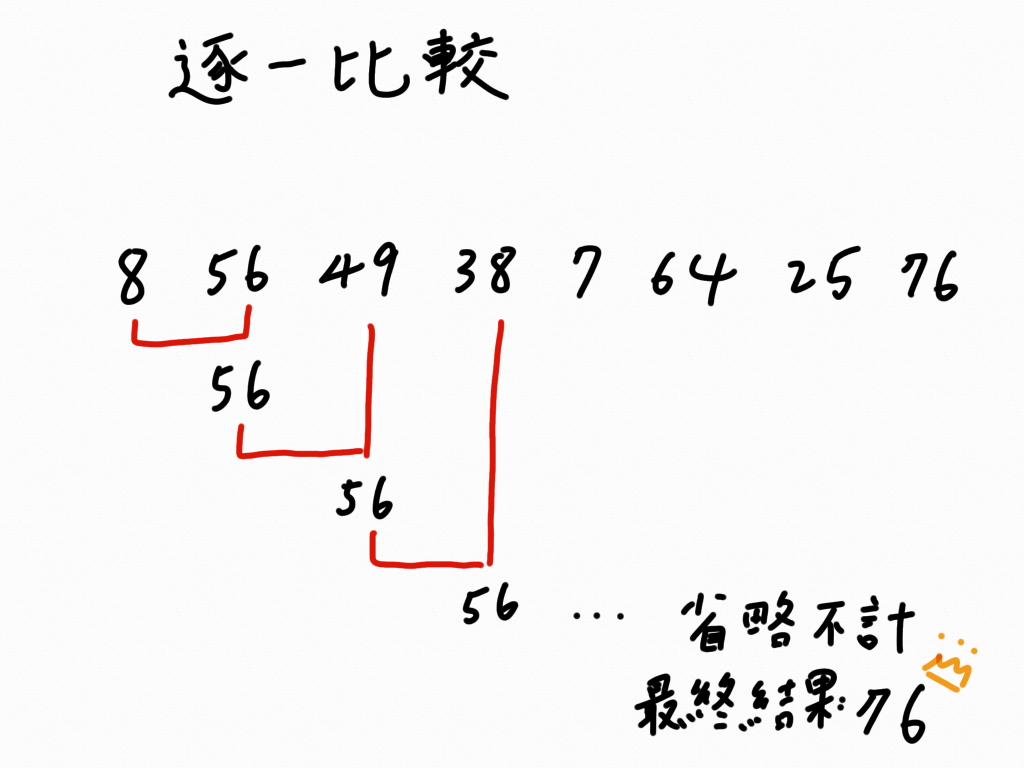
我們可以知道要在八個數裡找出「最大數」，總共要比較七次。同理可推，給定 n 個數，共要比較 n - 1 次才能找到「最大數」

▪「最小數」

• 步驟一：最大數扣除後，剩下七個數，分別為 8、56、49、38、7、64、25
• 步驟二：找到目前最小的數 8
• 步驟三：56 比 8 大，繼續一個一個比下去
• 步驟四：得到最小數為 7

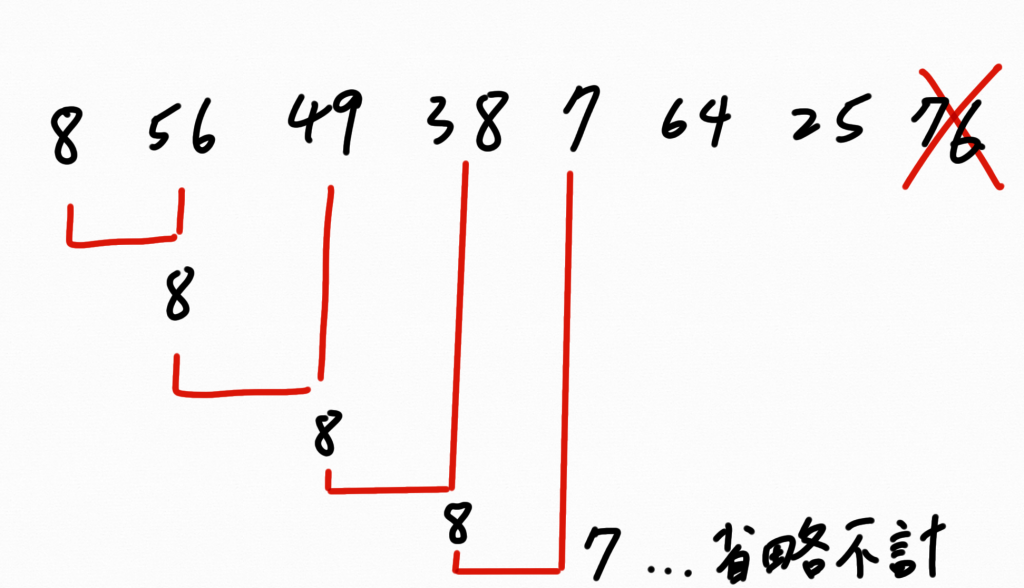
我們可以知道要在八個數裡找出「最小數」，總共要比較六次。同理可推，給定 n 個數，共要比較 n - 2 次才能找到「最小數」

在「逐一比較法」中，要找出「最大數」和「最小數」共需有比較 (n-1) + (n-2) = 2n - 1 次

說了那麼多來統整一下「逐一比較法」的特點：

• 比較每一個資料集合中的元素，然後根據比較結果調整它們的位置，直到整個數列排序完成
• 效率取決於所處理的資料集合大小，對於較大的資料集合，逐一比較法的時間複雜度可能會變得很高，效率較差
• 較適用於較小型的資料集合
• 最簡單的「逐一比較法」是氣泡排序（Bubble Sort），其時間複雜度為O(n^2)，其中n是數據集的大小

▌兩兩比較法

也稱為「相鄰元素比較法」，將比較大或小的數不斷兩兩比較，直到最後勝出的數為即為最大或最小數

舉例：請找出 8、56、49、38、7、64、25、76 這八個數裡的「最大數」和「最小數」

▪「最大數」

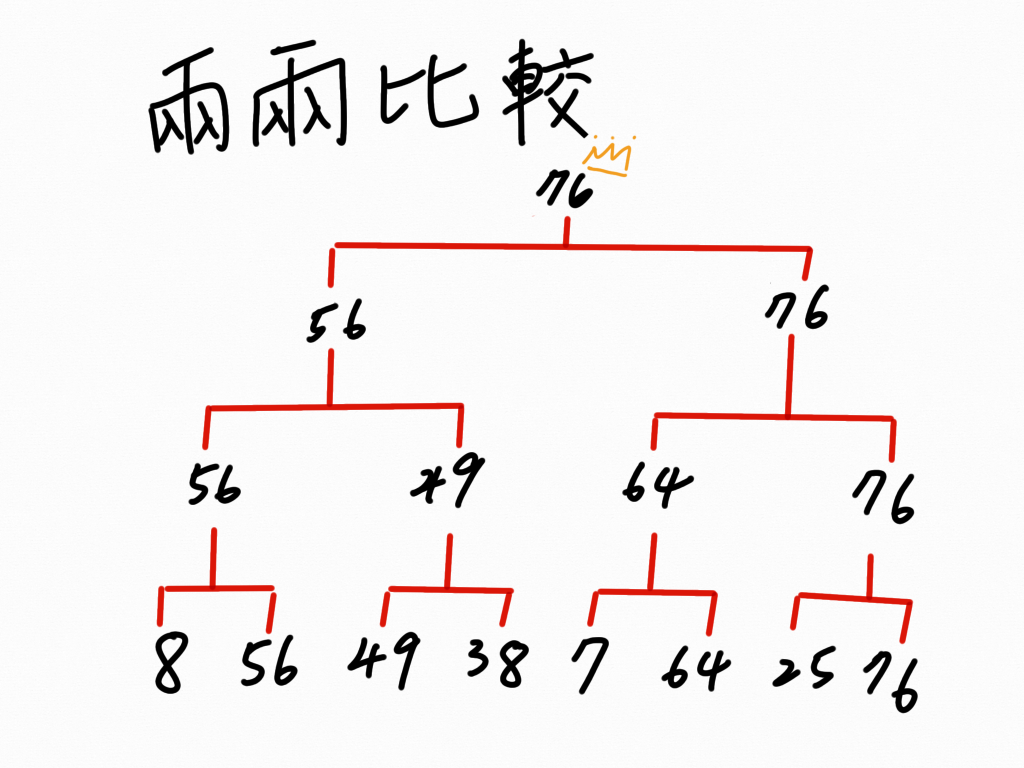
我們可以在上圖中得知，要在八個數裡找出「最大數」，共要比較七次。同理可推，給定 n 個數，共要比較 n - 1 次才能找到「最大數」，與「逐一比較法」相同

▪「最小數」

只要把第一輪兩兩比較中那些輸的數再做比較就可以，第一輪比較就是最下層那幾個數，比輸的有 8、38、7、25，共四個數，比較三次會得到最小數。同理可推，給定 n 個數，共要比較 n/2 - 1 次才能找到「最小數」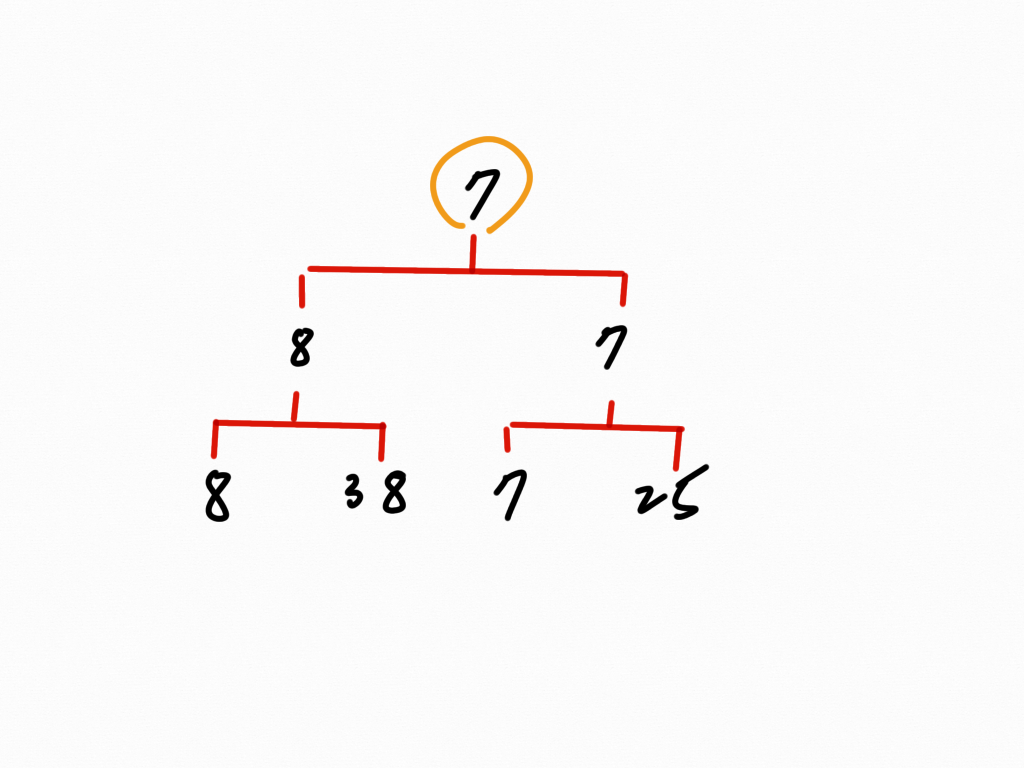

在「兩兩比較法」中，要找出「最大數」和「最小數」共需要比較，(n-1) + (n/2 - 1) = 3n/2 - 2 次

「兩兩比較法」的特點：

• 對資料集合中的每一對相鄰元素進行比較，然後根據比較結果調整它們的位置，直到整個數列排序完成
• 最簡單的兩兩比較法是插入排序（Insertion Sort），其平均和最壞情況的時間複雜度是O(n^2)。插入排序在小型數據集上的效率比氣泡排序好一點

▌總結

這兩種演算法的效率都較低，特別是對於大型資料集而言。如果需要處理大型的資料集，通常會更傾向使用其他更高效的演算法，如快速排序（Quick Sort）、合併排序（Merge Sort）或堆排序（Heap Sort），有較低的平均時間複雜度，通常是O(n log n)，會在後面篇章介紹

▌參考資料

1. 計算機概論 全華出版
2. 白話演算法 旗標出版
3. PJ - Big O Notion