▌合併排序法（Merge Sort）

「合併排序法」（Merge Sort）在 1945 年由馮紐曼（他真的是天才><）首次提出，跟「快速排序法」一樣都是一種分治法（Divide and Conquer)

▪ 什麼是分治法？

它的特性是將原本的問題拆解成兩個或多個較簡單的子問題，直至這些子問題可以簡單到直接求解。一般會經歷分割（Divide）、遞歸（Conquer）、合併（Merge）這些過程，以本篇要談論的「合併排序法」來說，過程如下：

1. 分割（Divide）、遞歸（Conquer）： 遞歸和分割在合併排序法中是一起工作的。分割會把長度為 n 的序列割成兩個大約相等的子數組(= 1/2 n)，直到每組都只有一個元素；遞歸則會呼叫自身來對這子數組進行排序

在這兩個遞歸呼叫中，每個子數組又會被分割成兩個更小的數組，然後合併排序函數會再次被遞歸地呼叫來對它們進行排序
2. 合併（Merge）：把兩邊排序好的陣列合併在一起

遞歸： 合併排序的函數會呼叫自身，在每次呼叫時都會對更小的數組進行排序
分割： 在每次遞歸調用中，數組會被分割成更小的部分

「分」為下圖藍色的部分；「治」為下圖黃色的部份

圖片來源

以下用 JS 來實現合併排序法，假設有一陣列 [38, 27, 43, 3, 9, 82, 10]，會先將陣列每次拆分成兩組同大小的子陣列，直到每組都只有一個元素再進行排序後合併

function mergeSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }

  const half = Math.floor(arr.length / 2);
  const left = arr.slice(0, half);
  const right = arr.slice(half);

  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  let result = [];
  let i = 0, j = 0;

  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) {
      result.push(left[i]);
      i++;
    } else {
      result.push(right[j]);
      j++;
    }
  }

  return result.concat(left.slice(i)).concat(right.slice(j));
}

const arr = [38, 27, 43, 3, 9, 82, 10]; // 原序列
const sortedArr = mergeSort(arr);
console.log(sortedArr); // [3,9,10,27,38,43,82] // 合併後的序列

▪ 執行時間

如果有 50 萬筆的資料，使用合併排序的執行時間如下

const arr = [];
for (let i = 0; i < 500000; i++) {
  arr.push(Math.floor(Math.random() * 500000));
}

const start = new Date().getTime();
const sortedArrs = mergeSort(arr);
const end = new Date().getTime();

const time = end - start;
console.log(`排序執行時間：${time}毫秒`); 

/* 
排序執行時間：240毫秒
排序執行時間：251毫秒
排序執行時間：273毫秒
*/

這個執行時間只是個參考，依照寫法的不同可能有不一樣的執行時間。上面的範例主要是想表達幾十萬筆資料，半秒鐘不到就可以排序完成，可見合併排序法在處理大型的資料量上是很快速的，且其時間複雜度在不同情況下皆為 O(n log n)，代表它十分穩定

▪ 時間複雜度：

• 最壞情況：O(n log n)
• 最佳情況：O(n log n)
• 平均情況：O(n log n)

▪ 空間複雜度

• O(n)

▌堆積排序法（Heap Sort）

▪ 什麼是堆（Heap）？

「堆」是一個完全二元樹（complete binary tree），完全二元樹的特點是除了最後一層，其他層的節點都是全滿的狀態，而且最後一層節點會全部靠左，如下圖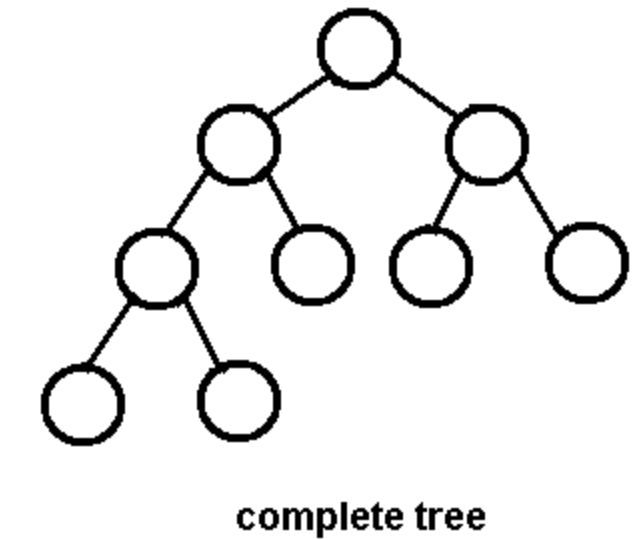

如果你對二元樹和節點沒有什麼概念可以參考這篇文章

• 樹狀結構 (Tree) - 你要了解的節點觀念
  https://ithelp.ithome.com.tw/articles/10336052

▪ 什麼是堆積排序（Heap Sort）？

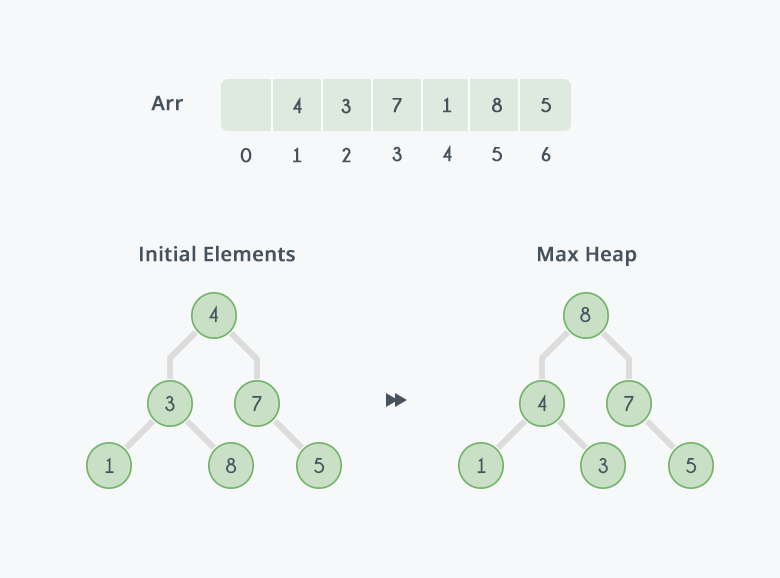
「堆積排序法」的特性是利用「堆積」資料結構的方法來進行排序，可以資料建立成 min-heap （最小堆）和 max-heap（最大堆），最大堆和最小堆的差別在於最大堆的根節點值總是會「大於」最小堆根節點的值！

• min-heap：以序列中「最小的值」當做根節點，並由小到大進行排序
• max-heap：以序列中「最大的值」當做根節點，並由大到小進行排序

圖片來源

執行的步驟可以初步分為兩階段：

1. 建立堆積（Heapify): 會將資料建構成「最小堆」或「最大堆」
2. 進行排序: 不斷從「堆」中取出最大（或最小）的元素一一進行排序，直到「堆」中的元素都被排除（eliminate）完
3. 最後會得到一個「由小到大」或是「由大到小」排序的序列

排序前的前置作業要把資料分為最大堆和最小堆，而在進行排序的過程中，包含「取出最大（或最小）元素」、「繼續排序」都不會佔用到額外的記憶體空間，都是在原數組中進行的，這也是為什麼堆積排序法也可以被視為一種原地（in-place）排序法。簡而言之，堆積排序會「重組」原數組來達到排序的目的，而不是創建一個新的數組

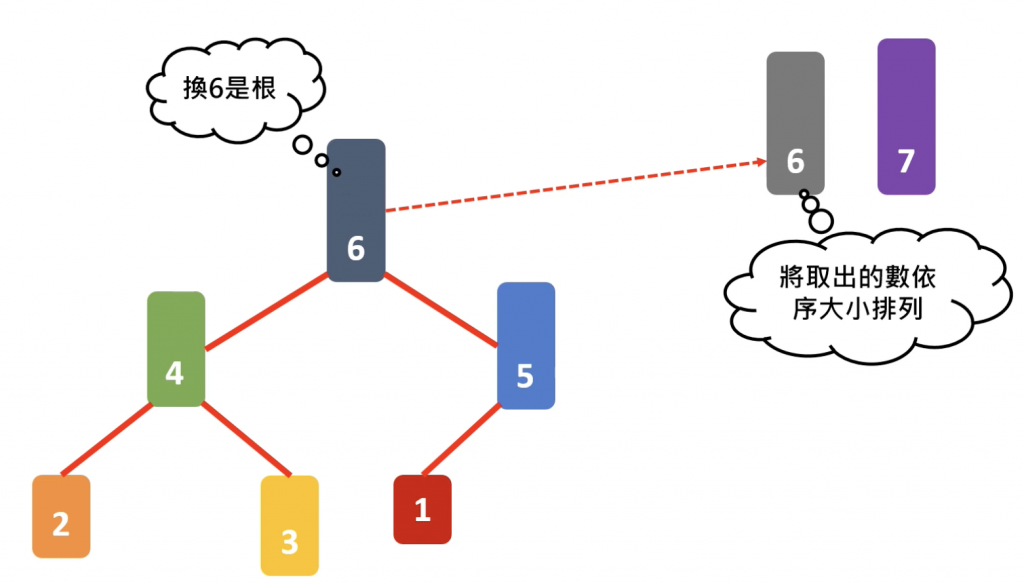
以下用 JS 來實現堆積排序法（以最大堆為例）

function heapify(arr, n, i) {
    let largest = i;
    let left = 2 * i + 1;
    let right = 2 * i + 2;

    if (left < n && arr[left] > arr[largest]) {
        largest = left;
    }

    if (right < n && arr[right] > arr[largest]) {
        largest = right;
    }

    if (largest !== i) {
        [arr[i], arr[largest]] = [arr[largest], arr[i]];
        heapify(arr, n, largest);
    }
}

function heapSort(arr) {
    let n = arr.length; // 9

    // 從最後一個非葉子節點開始，建立最大堆
    for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // 從最大堆中一一取出最大元素，並調整剩下的堆
    for (let i = n - 1; i >= 0; i--) {
        [arr[0], arr[i]] = [arr[i], arr[0]];
        heapify(arr, i, 0);
    }
}

let arr = [3, 1, 4, 1, 5, 9, 2, 6, 5];
heapSort(arr);
console.log(arr);  // [1, 1, 2, 3, 4, 5, 5, 6, 9]

▪ 執行時間

如果有 50 萬筆的資料，使用堆積排序的執行時間如下

// 5萬個隨機數字的數組
const tempArr = Array.from({ length: 50000 }, () => Math.floor(Math.random() * 50000));


const startTime = performance.now(); // 開始時間
heapSort(tempArr) // 執行堆積排序
const endTime = performance.now(); // 結束時間

const time = endTime - startTime;

console.log(`排序執行時間：${time}毫秒`); 

/* 
排序執行時間：14毫秒
排序執行時間：18毫秒
排序執行時間：22毫秒
*/

圖片來源

▪ 時間複雜度：

• 最佳情況：O(n log n) 或 O(n) (每個元素值都一樣時)
• 平均情況：O(n log n)
• 最壞情況：O(n log n)

▪ 空間複雜度

• O(1)
  因為堆積排序法為原地排序法，不會佔用到額外記憶體空間來保存排序過程中的中間結果，因此只需要固定的儲存空間來儲存變數（像是索引或是臨時變數等），這就確保了其空間複雜度是常數

▌總結

希望這篇能讓你對這兩種排序法有初步的了解～
「合併排序法」相較於「堆積排序法」來說更為穩定，而「堆積排序法」會被認為是不穩定的排序算法，是因為像是在有相同值元素的情況下，在建堆和調整堆的過程中，順序可能會被改變。這與其他穩定的排序算法（例如氣泡排序、合併排序等）有所不同，後者保證相同元素的相對順序不會被改變。

▌參考資料

1. 演算法介紹
2. Heap Sort 英文
3. Heap Sort 中文