排序是電腦很常用到的演算法也是很經典的演算法種類，排序相關的演算法如下：

▌選擇排序法（Selection Sort）

算是比較簡單的排序演算法。會在「未排序」的數列中找到最小（或最大）的元素，並將其移到「最左邊」

「選擇排序法」會將數列拆分成兩部分：

• 已排序：可選擇用「遞增」或「遞減」的方式來排列，就取決於你的需求了
• 未排序：找出「最小/最大的數」，將它和最前面的數對調。這個數不會小於已排序的的任何數，而且也不會大於未排序的任何數。對調完後可以把它歸入已排序的數列中

▪ 畫成圖如下：

圖片來源

▪ 拆解成步驟如下：

1. 找出「未排序」部分中的最小（或最大）元素

2. 將此元素與「未排序」部分的第一個元素交換位置。交換完後，此元素就可以被歸納為「已排序」的部分

其實主要就是一直在重複步驟 1 ~ 2，直到「未排序」部分為空。每次循環後，「已排序」部分就會增加一個元素，「未排序」部分會相對減少一個元素，最終達到整個數列排序的目的

「選擇排序法」的「時間複雜度」是 O(n ^ 2) ，對於較大的資料量來說，效率可不是非常好。如果對 Big O Notation 不是很了解，可參考昨天寫的這篇文章開頭部分

下面附上 JS 實現「選擇排序法」的範例程式，使用到了兩層迴圈

function selsectionSort(arr) {
  for(let i = 0; i < arr.length -1; i ++) {
    let minIdx = i;
    for(let j = i + 1; j < arr.length; j++) {
      if(arr[minIdx] > arr[j]) {
        minIdx = j;
      }
    }
    [arr[i], arr[minIdx]] = [arr[minIdx], arr[i]];  // 使用解構賦值來交換
  }
  console.log(arr); // [1,7,8,10]
  return arr;
}
selsectionSort([1,10,7,8]);

▌插入排序法（Insertion Sort）

插入排序法一樣可以分為兩個部分，一個是「已排序」、「未排序」。將「未排序」數列中的「第一個」數持續插到「已排序」數列中的適當位置

▪ 畫成圖如下：

圖片來源

▪ 拆解成步驟如下：

1. 找到「未排序」數列中的「第一個」數。以上方的圖片來舉例，我們要將 [8,7,5,9,1,6,2,4,3] 做排序，第一個元素 "8" 是已排序的，所以「未排序」數列中的「第一個」數為 "7"
2. 由小到大插到「已排序」的數列中，這時陣列的排序為 [7,8,5,9,1,6,2,4,3]，其中 7, 8 代表已排序的陣列

其實，就是一直在重複步驟 1 ~ 2而已，直到「未排序」的陣列為空為止

下面附上 JS 實現「插入排序法」的範例程式，可看出也使用到了兩層迴圈
「插入排序法」的「時間複雜度」在最壞和平均的情況下是 O(n ^ 2)，透過 insert sort & select sort 我們可有大概推敲到 O(n ^ 2)會有兩層迴圈的特性，執行時間會以指數成長。對於較大型的資料而言，此也不是最佳的選擇

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) { // 未排序的資料
    let currentVal = arr[i];
    let j;
    for (j = i - 1; j >= 0 && arr[j] > currentVal; j--) { // 已排序的資料
      arr[j + 1] = arr[j];
    }
    arr[j + 1] = currentVal;
  }
  console.log(arr); // 輸出：[1, 2, 30, 40]
  return arr;
}

insertionSort([40, 30, 2, 1]); 

▌冒泡排序法（Bubble Sort）

冒泡排序法（或稱「泡沫排序法」）是比較相鄰的元素，一樣可以將數列分成「已排序」和「未排序」兩部分。從未排序的數列中找到第一個數，並開始往後兩兩比較，如果 比較小/較大 就 往前/往後 移動，直到未排序數列的第一個數為止！

泡沫/冒泡排序（Bubble Sort）之所以被稱為「泡沫/冒泡」，是因為在排序過程中，較大（或較小）的元素會像泡沫一樣「浮」到數列的一端。相鄰的元素會被反覆地比較和交，如果一個元素比它旁邊的元素大（在遞增排序中），那麼這兩個元素就會被交換，不斷反覆進行這個過程

▪ 畫成圖如下：

▪ 拆解成步驟如下：

1. 一開始整個數列被歸納為「未排序」
2. 找出第一個數，以上圖為例就是 "5"
3. 並把他跟後面相鄰的元素 1 做比較，由於 5 比 1 大，所以 5 和 1 就會交換位置，接下來再繼續跟下一個相鄰元素 "4" 做比較，直到比到有數比當前元素還要大為止
4. 再回到步驟一，重複這個過程

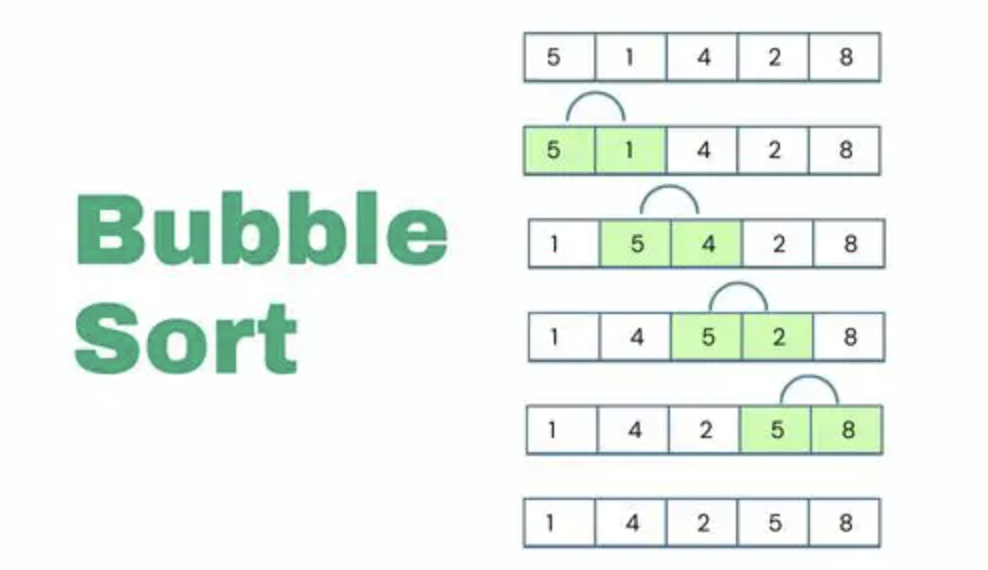
範例是以「遞增」方式來排序數列，如果是「遞減」，一樣從第一個數開始比較，只是遇到比較大的數要往左邊放

附上 JS 實現冒泡排序法「遞增」排列的範例程式。「冒泡排序法」的「時間複雜度」是 O(n ^ 2)，因此也不適合大型的資料

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - 1 - i; j++) { 
    // 上面減去 i 是因為在外層迴圈執行完一輪後，最大的元素會被推到數列的末端，就不再需要與它進行比較了
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  console.log(arr); // [1, 2, 3, 4]
  return arr;
}

bubbleSort([4, 3, 2, 1]);

▌快速排序法（Quick Sort）

比起前面的演算法，快速排序比較難懂一點。使用了分治法 把一個複雜的問題分成兩個或更多的相同或相似的子問題，直到最後子問題可以簡單的直接求解，原問題的解即子問題的解的合併，這也是它效率比較好的原因。（這邊我是截自維基百科，怎麼覺得有點繞口@@）

▪ 畫成圖如下：

圖片來源

▪ 拆解成步驟如下：

1. 先挑選數列中的任一個元素作為基準值（Pivot），以上圖中是挑了 "8"
2. 分割（Partitioning）：重新排列數組，所有比基準值小的元素放在基準值的前面; 比基準值大的元素放在基準值的後面。這邊你可能會看到 PivotIndex，這個詞，用來表示基準值在數列中的位置
3. 遞迴（Recursive）：對基準值左側和右側的兩個子數組重複以上的步驟

附上 JS 實現「快速排序法」的範例程式
在最差和平均的情況下，「快速排序法」有不同的時間複雜度。在最差的情況中執行時間為 O(n ^ 2)，就跟選擇排序法一樣；平均情況下的執行時間為 O(n log n)。會有這樣的差異來自於基準值的選擇，也就是當基準不斷的遇到最大或最小元素時，執行時間就會比較慢

function quickSort(arr) {
  if (arr.length <= 1) return arr; // 如果陣列長度 <1，就沒什麼好排列的
  
  const pivot = arr[0]; // 選擇第一個元素作為基準
  const left = []; // 存放比基準點小的元素
  const right = []; // 存放比基準點大的元素

  for (let i = 1; i < arr.length; i++) {
    arr[i] < pivot ? left.push(arr[i]) : right.push(arr[i]);
  }
   
  return quickSort(left).concat(pivot, quickSort(right));  // [1, 1, 2, 3, 6, 8, 10]
}

quickSort([3, 6, 8, 10, 1, 2, 1]); 

▌總結

以上介紹的這些排序演算法在不同的情況下具有不同的效能、特性。選擇排序法、插入排序法通常不太適合用在於大型資料集上，反而快速排序法會更適合，不過選擇一個好的基準值是快速排序法的效率好壞關鍵

▌參考資料

1. Searching & Sorting
2. 計算機概論 全華出版 & 白話演算法 旗標出版
3. 初學者學演算法