前言

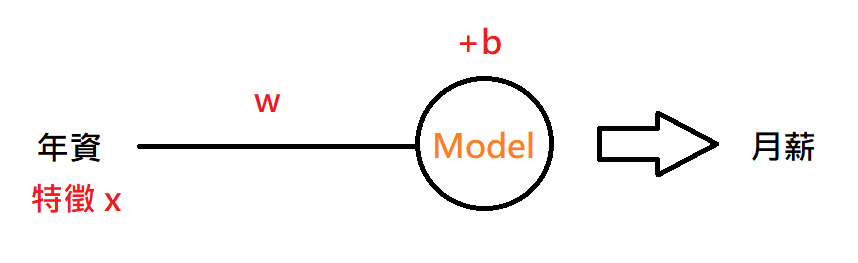
前面理論的東西講了這麼多，大家想必很想動手實作了吧，今天我們就要來著手搭建簡單線性回歸模型，我們要能夠輸入年資 ( 特徵 ) 並讓這個模型根據輸入的資訊去預測月薪，模型架構如下：

使用套件

下面是搭建模型所需的套件：

import pandas as pd # 用來做資料處理
import matplotlib.pyplot as plt # 繪製座標圖
from ipywidgets import interact # 座標圖互動效果
import numpy as np # 方便做陣列的運算

資料集

到下面提供的連結可以下載到資料集的部分，其特徵欄位名稱為 YearExperience，標籤欄位名稱為 Salary：

https://drive.google.com/file/d/1xGN9Hp6IGz2RmGnv7X8w3cpyxVcc2sXy/view?usp=drive_link

下面程式碼我們先讀取資料集 csv 檔，再將檔案中的特徵與標籤欄位 YearsExperience 和 Salary，分別設給變數 x 跟 y，兩者皆為 Series 物件，分別存放特徵與標籤欄位資料：

df = pd.read_csv("Salary_Data.csv")
x = df["YearsExperience"] # 特徵
y = df["Salary"] # 標籤

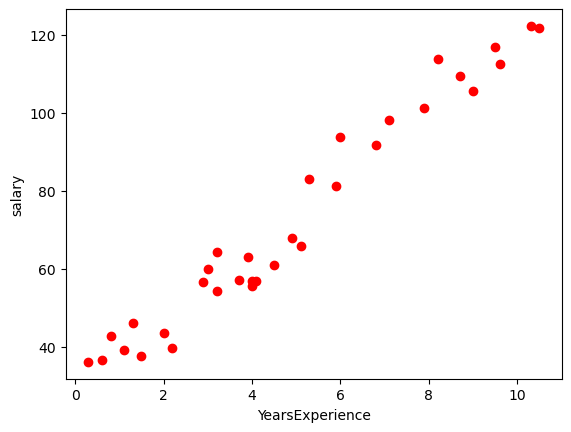
而我們必須要設計出一個 model，只要 input 年資它就會 output 預測的月薪，下面程式碼先把每筆訓練資料 ( 真實結果 ) 都畫到圖上 ( 每個點都是一筆資料 )，x 軸為年薪，y 軸為月薪：

plt.scatter(x, y, color="blue")
plt.xlabel("YearsExperience")
plt.ylabel("salary")
plt.show()

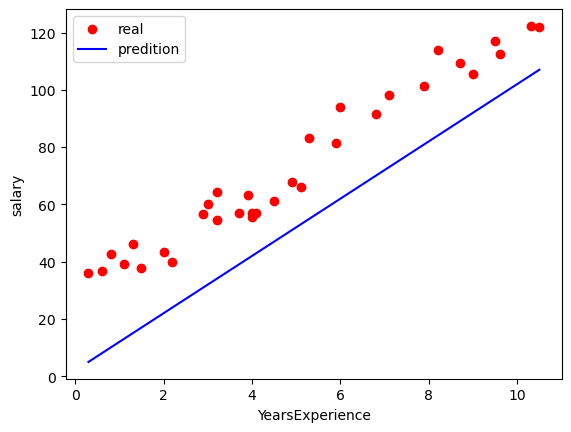
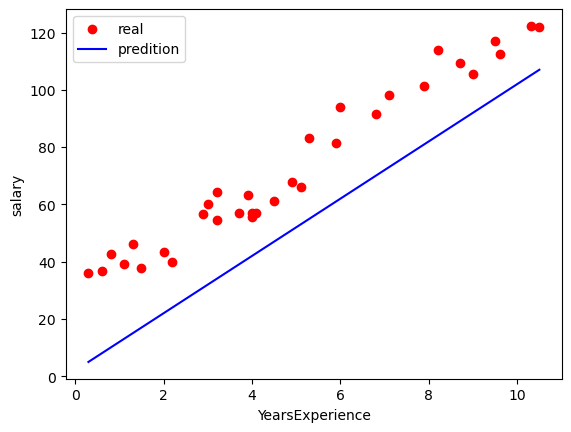
再來就要設計一個用來預測的 model，其實就是一條線 ( y_pred )，如果線越接近真實結果 ( 下圖中紅點 ) 就代表預測的越準確 ( 模型越好 )，因此下面程式碼中就定義 model 為 y_pred = w * x + b，讓 Input ( x ) 和 Output ( y_pred ) 之間存在著 Linear 的關係，然後再透過調整 model 參數 ( w、b ) 來讓我們的 model ( y_pred ) 更接近真實結果，而不同的參數也會影響到 model 的成本 ( 後面談到 )，下圖就是參數 ( w , b ) = ( 10 , 2 ) 時的模型，顯然和真實結果還是差了點距離：

w = 10 # 調整參數
b = 2 # 調整參數
y_pred = w * x + b # 定義的模型 function (model)
plt.scatter(x, y, color="red", label="real") # 真值資料
plt.plot(x, y_pred, label="predition") # 預測結果
plt.legend()

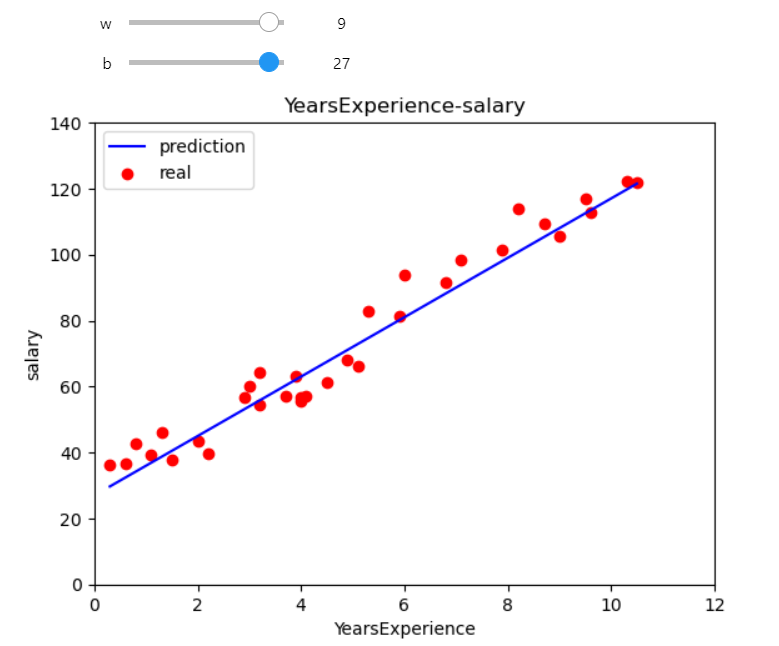
而為了要接近真實結果就得不斷調整參數 ( w、b )，這樣其實很累人又沒效率，因此下面程式碼就用了 interact ( ) 這個互動函數來幫助我們和座標圖互動，只要給它自定義的繪圖函數 ( plot_pred )，在這個函數裡面必須要有座標圖的存在，然後設定 w 和 b 為函數 Input 再設定值的範圍為 0 ~ 10，這樣就可以在這個範圍中任意滑動搖桿調整輸入參數並控制模型輸出至最接近真實結果，不用再反覆修改程式碼中的參數：

# 自定義繪圖函數
def plot_pred(w, b):
    y_pred = w * x + b # model
    plt.plot(x, y_pred, color="blue", label="prediction") 
    plt.scatter(x, y, color="red", label="real", marker="o")
    plt.xlabel("seniority")
    plt.ylabel("salary")
    plt.title("seniority-salary")
    plt.legend()
    plt.xlim([0, 12])
    plt.ylim([0, 140])
    plt.show()
interact(plot_pred, w=(0, 10, 1), b=(0, 30, 1))

成本 ( 損失 ) 函數

成本函數亦為損失函數，當我們所設計的 model 和真實結果差了一段距離，我們要知道到底差多少，就會用到 MSE 均方誤差 的方法來進行計算，可以用來求出 model 與真實結果之間的的相距成本，可以說這個損失函數是決定一個 model 好壞的標準，成本函數出來的值越高代表 model 越不準，反之越準確，MSE 損失函數公式如下：

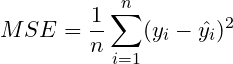
舉例來說，假設我們現在有 n 個真實結果 ( 上圖紅點 ) 和 model ( 上圖藍線 )，每個真實結果 在 model 上都會垂直對應點 ，兩點垂直相減再平方 ( 相減有可能為負 ) 就會得到兩點間距離，最後把每個 和每個 之間的距離計算其平均值就是這個 model 的損失成本。

回到今天我們做的 model ( y_pred )，model 的參數 ( w , b ) 的大小也會影響著成本大小，下面就是成本函數的實作，而我們求出成本 cost 後便把它平均 mean ( )，以免值太大：

def cost(w, b):
	y_pred = w * x + b # model
	cost = (y - y_pred) ** 2 
	return cost.mean() # 取成本平均值

上面程式碼中 cost.mean ( ) 的算法 :

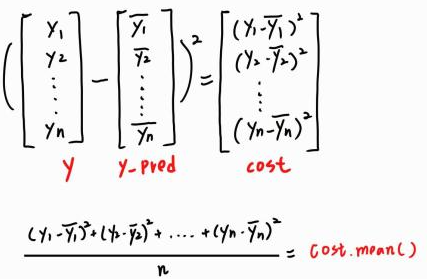
在得到了成本函數後，因為成本函數會受到參數的影響，我們就要來探討要取哪一組參數 ( w 跟 b )，才能夠使得這個 model 的成本最小，所以就必須要找到成本函數的最低點處的 w* 和 b* ( 最佳參數 )，找的方法有兩種，一個是暴力破解法，另個則是用梯度下降 Gradient Descent。

優化器

在機器學習中，優化器就是一種調整 model 參數使其成本函數最小 / 大的方法，常見的方式是透過迭代的更新參數值，不斷的減小成本以達到 model 最佳化的目標，這裡提到的優化器有暴力破解法和 梯度下降 Gradient Descent，並比較其差異：

暴力破解

暴力破解法是一種窮舉搜尋的方法，嘗試了所有可能的參數組然後計算每組的成本大小，最後使成本函數有最小值的參數組合，下面程式碼窮舉出 -100 ~ 100 的 ws 和 -100 ~ 100 的 bs，所以我們有 201 個 w 跟 201 個 b，所以最後會有 201 * 201 個參數組合，再宣告二維陣列 costs ( 成本矩陣 ) 來存放每組參數的成本，這部分的程式碼因為算法效率較低所以執行時間會較久：

窮舉出 201 個 w 跟 b

宣告存放每組參數成本的二維陣列 costs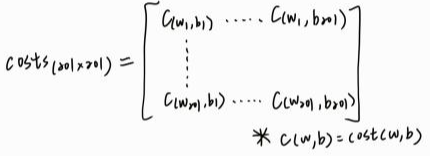

ws = np.arange(-100, 101) # 參數 w 範圍
bs = np.arange(-100, 101) # 參數 b 範圍
costs = np.zeros(shape=(201, 201)) # 存放參數組合的成本矩陣
i = 0
for w in ws:
    j = 0
    for b in bs:
        costs[i, j] = (cost(w, b)) # 算出該參數組合的成本並存入costs中
        j = j + 1
    i = i + 1

我們現在有了成本矩陣和參數的陣列 ws、bs，再透過 np.meshgrid ( ) 函數把參數陣列轉型就會得到參數矩陣 w_grid、b_grid，有這些矩陣就可以把三維的成本函數繪製出來，最後再把成本函數最小值 ( 最低點處 ) 的 w * 跟 b * 找出來：

plt.figure(figsize=(10, 10)) # 調整畫布大小
ax = plt.axes(projection="3d") # 建立三維座標圖
ax.view_init(15, 70) # 調整座標圖的仰角與旋轉角度
b_grid, w_grid = np.meshgrid(ws, bs) # 
ax.plot_surface(w_grid, b_grid, costs, cmap="Spectral_r", alpha=0.7) # 繪製圖形
ax.plot_wireframe(w_grid, b_grid, costs, color="black", alpha=0.1) # 繪製圖形框線
ax.set_title("cost function w-b")
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("cost")
w_index, b_index = np.where(costs == np.min(costs)) # 找出成本函數最小值的 w*、b* 位置
ax.scatter(ws[w_index], bs[b_index], costs[w_index, b_index], color="red") # 圖上點出最小值位置
print(ws[w_index], bs[b_index]) # 打印 w*、b*
plt.show()

# Ouput : [9] [29]

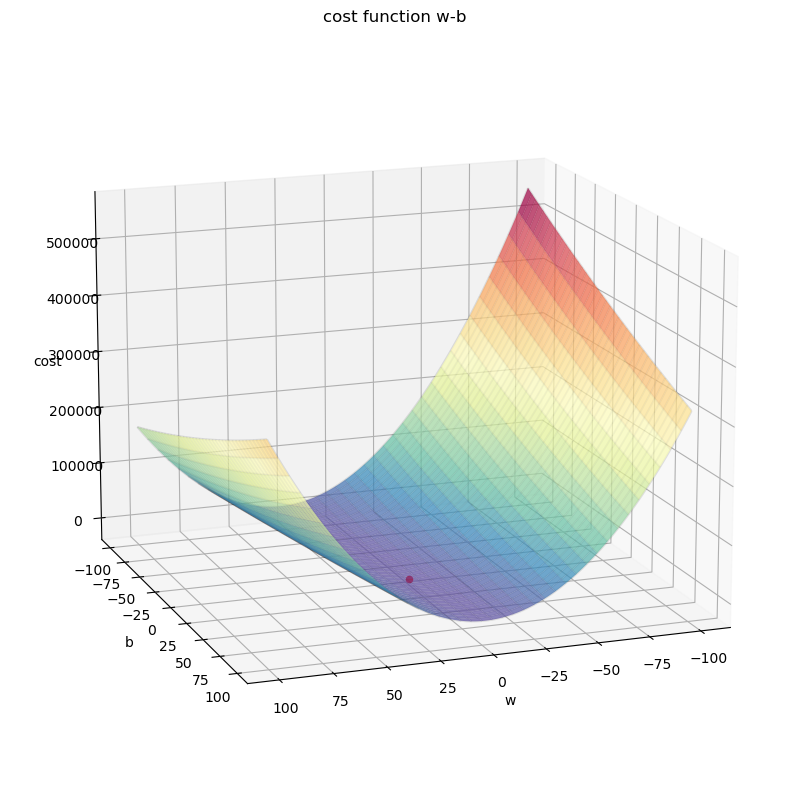
下圖為三維成本函數，紅點為函數的最低點 ( 最小值 )，那點存在著最佳參數 w*、b*：

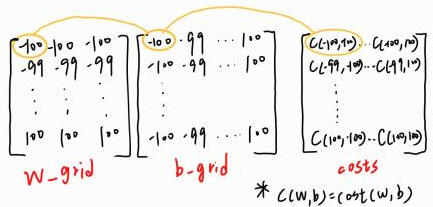
下面是 w_grid 和 b_grid ( w、b 參數矩陣 ) 和 costs ( 成本矩陣 ) 在繪圖時之間的對應關係和三維成本函數圖形 :

梯度下降 Gradient Descent

梯度下降是一種透過迭代來優化的算法，通過計算成本函數對於参数 ( w、b ) 的梯度，梯度就是由 w、b 方向導數分量 組成的向量，用來決定參數的更新方向。梯度下降會根據當前參數的梯度方向，沿着負梯度方向逐步調整參數值，直到找到最佳解。下面先定義一個求梯度的方法：

def gradient(w, b): # 求梯度
    w_gradient = (x * (y - (w * x) - b)).mean() # w 方向的導數
    b_gradient = ((y - (w * x) - b)).mean() # b 方向導數
    return w_gradient, b_gradient

計算梯度 w_gradient、b_gradient 偏微分的過程 :

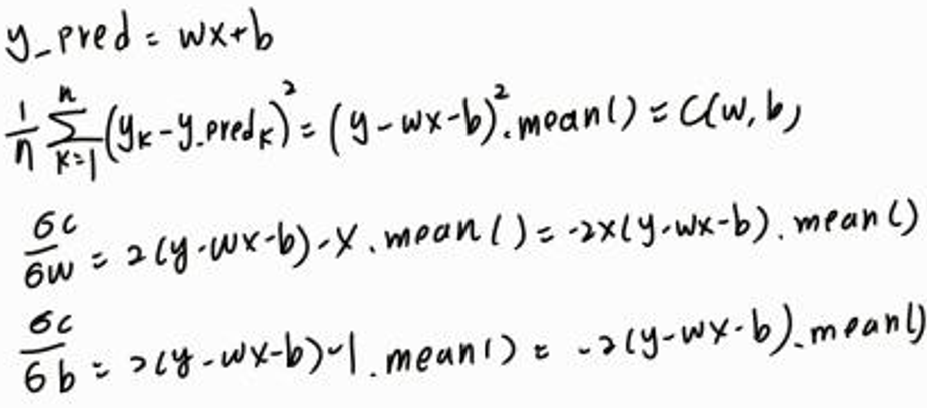
下面程式碼實作了梯度下降 ( Gradient Descent )，先決定一個起始參數，然後再讓參數依照梯度 ( Gradient ) 自己往函數的最低點方向移動，參數移動幅度大小會和斜率跟學習率 有關，w 參數的移動幅度公式 ， 是當前的 w，所以每個 都會等於上一個 w 再加上 ( )，w 值會經由迭代不斷更新直到 時該點 w 就是我們要找的最佳參數，而移動公式前面有一個 ，其大小可以自己設定，設的越大參數移動的幅度就越大，學習的速度也就愈快，反之 越小就越慢，而參數在移動的時候，因為要往最低點 ( 最小值 ) 處移動，所以該點上的斜率 > 0，就要讓參數往較小的地方走，若斜率 < 0 就要往較大的地方移動，所以移動幅度公式前面要加一個負號：

def gradient_descent(w_init, b_init, learning_rate, cost_func, gradient_func, run_iter, p_iter=1000):
    w = w_init # 設定初始 w
    b = b_init # 設定初始 b
    w_hist = [] # 存放更新後的 w
    b_hist = [] # 存放更新後的 b
    cost_hist = [] # 存放參數更新後的 cost
    for i in range(run_iter): # 進行迭代
        w_gradient, b_gradient = gradient_func(w, b) # 取得該點參數之斜率
        w_step = - learning_rate * w_gradient # 計算 w 方向移動幅度
        b_step = - learning_rate * b_gradient # 計算 b 方向移動幅度
        w = w + w_step # 更新 w
        b = b + b_step # 更新 b
        w_hist.append(w) # 紀錄更新後 w
        b_hist.append(b) # 紀錄更新後 b
        cost_hist.append(cost_func(w, b)) # 紀錄成本
        if(i % p_iter == 0): # 每隔幾次就 print 出來第當次迭代的次數、參數、參數的成本、參數斜率並調整印出格式
            print(f"time:{i:5}, cost:{cost_func(w, b): .4e}, w:{w: .2e}, b:{b: .2e}, w_gradient:{w_gradient: .2e}, b_gradient:{b_gradient: .2e}")
    return w, b, w_hist, b_hist, cost_hist

learning_rate = 1e-3 # 設定學習率
w_final, b_final, w_hist, b_hist, cost_hist = gradient_descent(-100, -100, learning_rate, cost, gradient, 20000, 1000)
print(f"final: w = {w_final:.2f}, b = {b_final:.2f}")

最終執行的結果並得到最佳解 ( w , b ) = ( 9.12 , 28.01 )，在一次次的迭代過程中，參數 w 和 b 會不斷地去做更新的動作，慢慢往梯度為 0 ( 最低點 ) 的地方去移動，每次迭代時參數都會更加接近損失函數最小值處，直到已達設定的迭代次數為止，而此時的參數就代表模型經過訓練後所得到的最佳參數，也就是下面輸出結果的 w = 9.12 與 b = 28.01：

time:    0, cost: 4.7317e+05, w:-9.16e+01, b:-9.87e+01, w_gradient:-8.40e+03, b_gradient:-1.32e+03
time: 1000, cost: 1.1491e+03, w: 1.87e+01, b:-3.60e+01, w_gradient: 5.13e+00, b_gradient:-3.42e+01
time: 2000, cost: 4.1627e+02, w: 1.48e+01, b:-9.49e+00, w_gradient: 3.01e+00, b_gradient:-2.00e+01
time: 3000, cost: 1.6436e+02, w: 1.24e+01, b: 6.02e+00, w_gradient: 1.76e+00, b_gradient:-1.17e+01
time: 4000, cost: 7.7765e+01, w: 1.11e+01, b: 1.51e+01, w_gradient: 1.03e+00, b_gradient:-6.89e+00
time: 5000, cost: 4.8000e+01, w: 1.03e+01, b: 2.05e+01, w_gradient: 6.06e-01, b_gradient:-4.04e+00
time: 6000, cost: 3.7769e+01, w: 9.79e+00, b: 2.36e+01, w_gradient: 3.55e-01, b_gradient:-2.37e+00
time: 7000, cost: 3.4252e+01, w: 9.51e+00, b: 2.54e+01, w_gradient: 2.08e-01, b_gradient:-1.39e+00
time: 8000, cost: 3.3043e+01, w: 9.35e+00, b: 2.65e+01, w_gradient: 1.22e-01, b_gradient:-8.14e-01
time: 9000, cost: 3.2627e+01, w: 9.26e+00, b: 2.71e+01, w_gradient: 7.16e-02, b_gradient:-4.77e-01
time:10000, cost: 3.2485e+01, w: 9.20e+00, b: 2.75e+01, w_gradient: 4.20e-02, b_gradient:-2.80e-01
time:11000, cost: 3.2436e+01, w: 9.17e+00, b: 2.77e+01, w_gradient: 2.46e-02, b_gradient:-1.64e-01
time:12000, cost: 3.2419e+01, w: 9.15e+00, b: 2.78e+01, w_gradient: 1.44e-02, b_gradient:-9.61e-02
time:13000, cost: 3.2413e+01, w: 9.14e+00, b: 2.79e+01, w_gradient: 8.46e-03, b_gradient:-5.64e-02
time:14000, cost: 3.2411e+01, w: 9.13e+00, b: 2.79e+01, w_gradient: 4.96e-03, b_gradient:-3.30e-02
time:15000, cost: 3.2410e+01, w: 9.13e+00, b: 2.80e+01, w_gradient: 2.91e-03, b_gradient:-1.94e-02
time:16000, cost: 3.2410e+01, w: 9.13e+00, b: 2.80e+01, w_gradient: 1.71e-03, b_gradient:-1.14e-02
time:17000, cost: 3.2410e+01, w: 9.13e+00, b: 2.80e+01, w_gradient: 1.00e-03, b_gradient:-6.66e-03
time:18000, cost: 3.2410e+01, w: 9.12e+00, b: 2.80e+01, w_gradient: 5.86e-04, b_gradient:-3.90e-03
time:19000, cost: 3.2410e+01, w: 9.12e+00, b: 2.80e+01, w_gradient: 3.44e-04, b_gradient:-2.29e-03
final: w = 9.12, b = 28.01

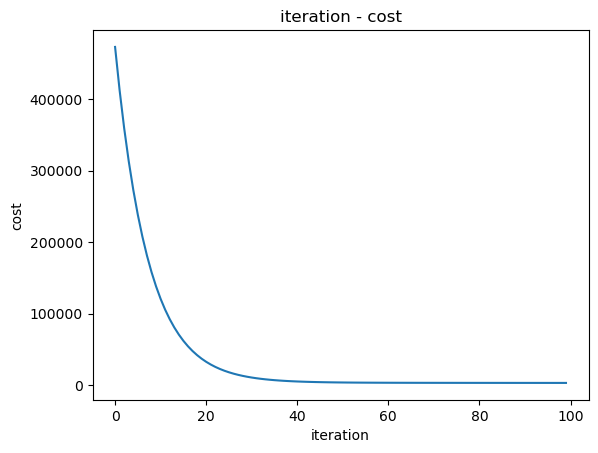
迭代次數與成本的關係圖 :

plt.plot(range(100), cost_hist[:100]) # 迭代次數 100 以內
plt.title("iteration - cost")
plt.xlabel("iteration")
plt.ylabel("cost")
plt.show()

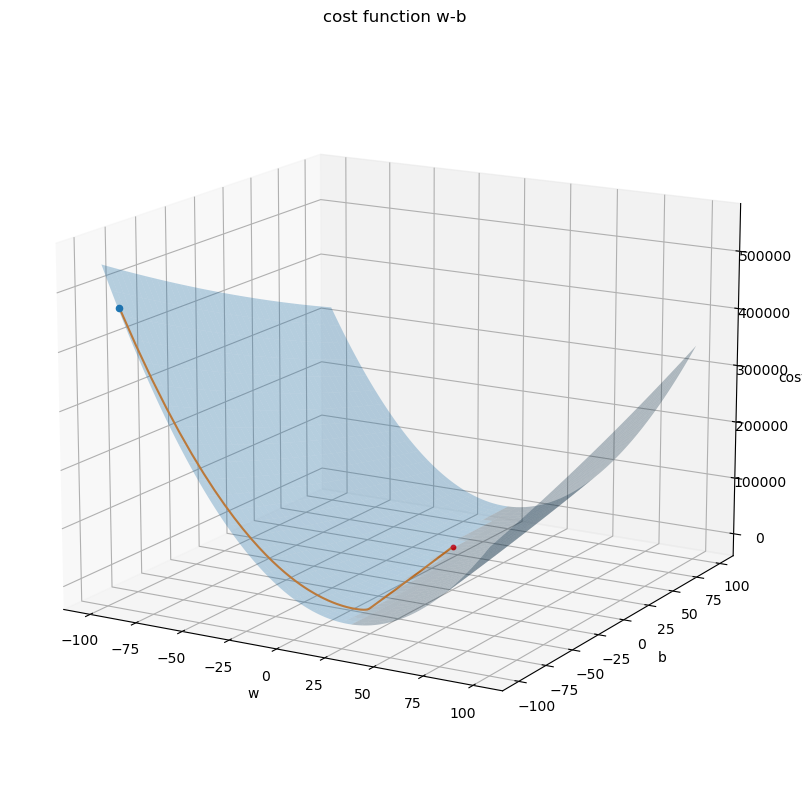
將執行梯度下降方法時參數移動的路徑畫在圖上，會發現參數會逐漸往最低點處移動 :

plt.figure(figsize=(10, 10))
ax = plt.axes(projection="3d")
ax.view_init(15, -60)
b_grid, w_grid = np.meshgrid(ws, bs)
ax.plot_surface(w_grid, b_grid, costs, alpha=0.3)
ax.set_title("cost function w-b")
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("cost")
w_index, b_index = np.where(costs == np.min(costs))
ax.scatter(ws[w_index], bs[b_index], costs[w_index, b_index], color="red", s=10)
ax.scatter(w_hist[0], b_hist[0], cost_hist[0]) # 第一次迭代更新時的參數和成本
ax.plot(w_hist, b_hist, cost_hist) # 參數移動路徑
plt.show()

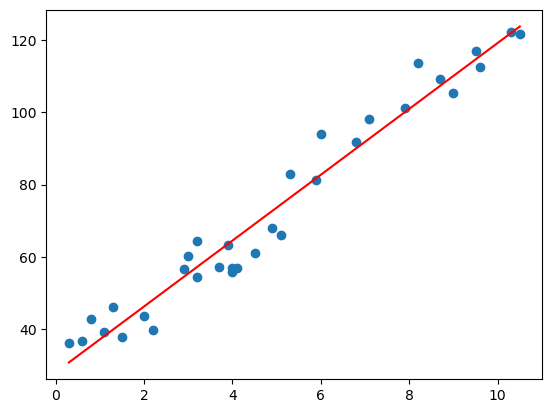
終於到了最後一步，就是把我們經過梯度下降找出的最佳模型參數代入到 model，其預測出來的線 ( 下圖紅線 ) 和真實結果 ( 下圖藍點 ) 做比對就可以知道 model 預測的真確性

plt.scatter(x, y) # 真實結果
plt.plot(x, w_final * x + b_final, color="red") # 模型線
plt.show()

比較暴力破解法與梯度下降

暴力破解適合用於參數空間較小，問題規模較小的情況，能夠找到絕對極小值，但它的計算複雜度極高，對於大規模問題往往不切實際。相較之下，梯度下降法適合用於大規模問題，可以高效的找到全域最佳解，在實際應用中，梯度下降通常是機器學習中求解最佳參數的常用方法，因為它能夠在合理的時間內找到最佳的解決方案。

小結

今天我們學到：

• 搭建簡單線性回歸模型與訓練
  • 使用暴力破解方法
  • 使用梯度下降方法
• 繪出模型在迭代過程中成本的變化
• 繪出梯度下降過程中參數的移動路線

我們下篇文章見 ~

參考資料

https://www.youtube.com/watch?v=wm9yR1VspPs

GrandmaCan-我阿嬤都會 - 機器學習課程