有系統地辨識和糾正錯誤

上一節為我們提供了一種對任何訊息進行編碼的方法 𝑚 變成一個碼字 𝑐。 這可以推廣到任何代碼。現在，我們討論一種系統方法來識別並可能糾正透過雜訊通道發送碼字時發生的錯誤。

假設鮑伯收到了該區塊 𝐜̃ 。該塊可能會也可能不會以某種方式被損壞。每個代碼對於它可以正確識別並隨後糾正的錯誤數量都有一定的容忍度。看到它的方法就是回憶一下 𝐜̃ = 𝐜 + 𝐞。誤差向量 𝐞 是 𝑛 位長，所以有 2𝑛 可能的錯誤。碼字 𝐜 其中儲存了一些資訊以幫助識別錯誤。但它還必須儲存訊息本身。所以從 𝑛 中的資訊位 𝐜 , 𝑘 資訊位正在儲存訊息，而 𝑛 - 𝑘
訊息位可用於識別錯誤。所以，程式碼最多可以識別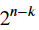不同的錯誤。例如，重複程式碼可以識別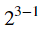= (四種不同的錯誤 - 要麼沒有錯誤，要麼恰好在三個位之一上出現錯誤)。類似地，漢明碼可以識別 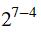= 八個不同的錯誤。

這裡的一般流程是什麼？我們在漢明程式碼範例中看到，我們將訊息的一些一致性檢查儲存為代碼字的一部分。我們說過前四位必須遵守一些奇偶校驗。一般來說，在任何線性程式碼中，都會有一些一致性檢查，並將由碼字上元素的線性方程組給出。這些方程式由碼字相乘的矩陣指定，並給出如下。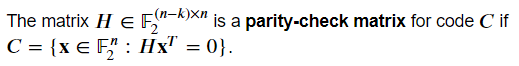

此定義表示程式碼由滿足約束的程式碼空間的所有元素組成 𝐻=0 。由於有 𝑛 - 𝑘 行到該矩陣，矩陣放置 𝑛 - 𝑘 程式碼空間元素的約束，留下一個 𝑛 − ( 𝑛 − 𝑘 ) = 𝑘 維空間。請注意，線性方程組可以線性變換為另一組等效方程式。因此，奇偶-慈善矩陣並不唯一。行操作將產生相同程式碼的其他奇偶校驗矩陣。

奇偶校驗矩陣中的限制顯然並不獨立於生成矩陣，因為生成矩陣包含有關代碼的所有資訊。

Error syndrome

我們已經了解到奇偶校驗矩陣可用於確定是否 𝐜̃ 是否是碼字。但是我們如何計算發生了哪個錯誤。想像一下愛麗絲發送代碼字 𝐜 它被扭曲為 𝐜̃ = 𝐜 + 𝐞 。現在，奇偶校驗矩陣的效果是，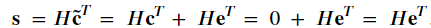

數量 𝐬 稱為錯誤綜合症(error syndrome)，並且是長度向量 𝑛 - 𝑘 。有 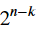可能的錯誤綜合症。我們在上面討論過，經典線性碼最多只能修正 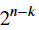錯誤。每個可糾正的錯誤對應於一個不同的錯誤綜合症。
例如，對於漢明碼， 𝐬 長度為3，並且有8種不同的綜合症對應於不同的零位或一位錯誤。

Distance of code

在討論程式碼時，一個重要的重點是它們的距離。距離決定了可以糾正的錯誤數量。每當代碼字發生錯誤時 𝐜 ，它會創造一個損壞的碼字 𝐜̃ 距離有一定的“距離” 𝐜 。如果距離很小，那麼仍然可以修正錯誤，但是如果距離大於某個值，則無法修正錯誤。此閾值稱為代碼的距離。我們將其形式化如下。

Hamming Distance

漢明距離（不要與漢明碼混淆；漢明只是一位有許多成就的科學家）將用於建立程式碼距離的概念。

兩個位元串之間的漢明距離 𝐬 , 𝐭 是它們具有不同符號的地方的數量。這將被表示為（𝑠 ，𝑡 ）

漢明距離決定了所需替換或錯誤的數量使得將長度- 𝑛的𝐬 轉換成另一個長度— 𝑛 向量 𝐭 ，反之亦然。因此，對於我們的目的來說，這是一個非常自然的定義。漢明距離可以計算為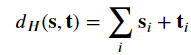

其中加法是在二進位字段中進行的，但求和是常規整數加法。

例如， 1011 和 0111 之間的距離是二。您必須翻轉前兩個才能從第一個轉到第二個，反之亦然。

參考資料:https://github.com/abdullahkhalids/qecft