前言

今天(2023/11/18)馬英九基金會公布藍白合民意調查的統計結果，雙方未達成共識，癥結點在於統計誤差認知有不同見解，到底統計誤差應該是3%或6%，我們就從統計學的角度說明，本文純就學術探討，無意捲入政治爭論。

理論基礎

假設柯文哲支持度 > 侯友宜支持度的機率為p，反之，為1-p，是標準的『伯努利分配』(Bernoulli distribution)，相關統計量如下：
平均數(μ) = p
標準差(σ) =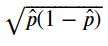

若柯文哲、侯友宜贏的機率是均等的，即p=0.5，依照上述公式計算 μ = 0.5，σ = 0.5，驗算如下：

std = (0.5 * 0.5) ** (1/2)
# 執行結果： std = 0.5

假設檢定

柯文哲主張：

若民意調查在統計誤差範圍內，即算侯友宜贏。
換句話說，柯文哲若未『顯著』勝過侯友宜，柯文哲就認輸了。

何謂『顯著』(Significant)? 要檢驗柯文哲是否『顯著』勝過侯友宜，通常會採用假設檢定(Hypothesis Testing)，訂定兩種假設：
對立假設 H1：柯文哲支持度(μ1) > 侯友宜支持度(μ2)
虛無假設 H0：柯文哲支持度(μ1) <= 侯友宜支持度(μ2)

依據中央極限定理(Central Limit Theorem)，有兩個重要的假設：

1. 即使原始資料不是常態分配，只要樣本數夠大，樣本平均數(μ)就會趨於常態分配(normal distribution)，因此，不論何種機率分配的資料都可以使用常態分配來檢定(z或t檢定)。
2. 平均數(μ)的標準差(σ)，又稱為『標準誤差』(Standard error)，要額外除以n開根號，公式如下：
   
   n:樣本數。

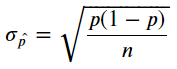
具備以上知識，就可以進行假設檢定了，檢定前要先設定『顯著水準』，一般會訂為5%，也可以說95%信心水準，以下圖常態機率分配說明：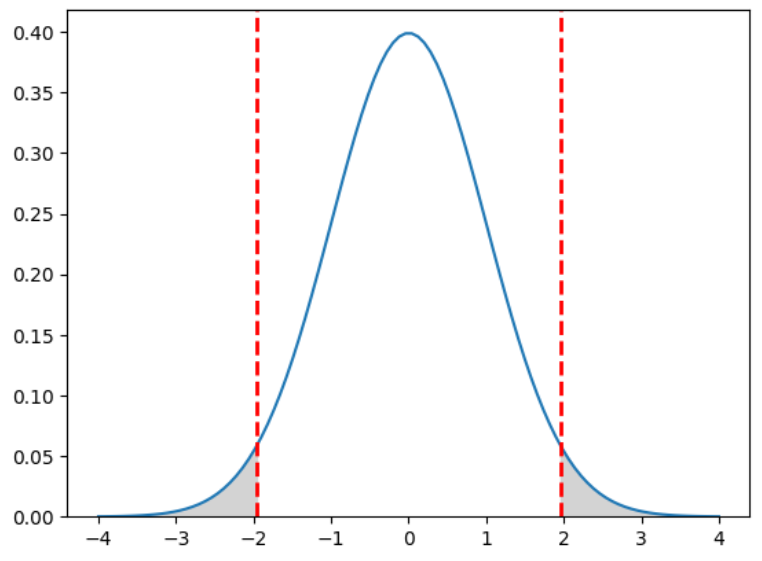

圖一. 5%顯著水準

亦即介於[μ-1.96σ, μ+1.96σ]的機率總和為95%，兩個灰色區域面積的機率和為5%，灰色區域稱為拒絕域，落入左邊灰色區域表示『柯文哲支持度顯著小於侯友宜支持度』，落入右邊灰色區域表示『柯文哲支持度顯著大於侯友宜支持度』，也就是說民調結果的統計量沒有掉入右邊灰色區域，柯文哲就認輸。

以下圖為例，大於紅線的藍色面積為5%，調查結果的統計量(紫線)如果在紅線(μ+1.96σ)右邊，就表示『柯文哲支持度顯著大於侯友宜支持度』，反之，若調查結果的統計量在紅線左邊，表示『柯文哲【未】顯著大於侯友宜支持度』，侯柯配就成局了。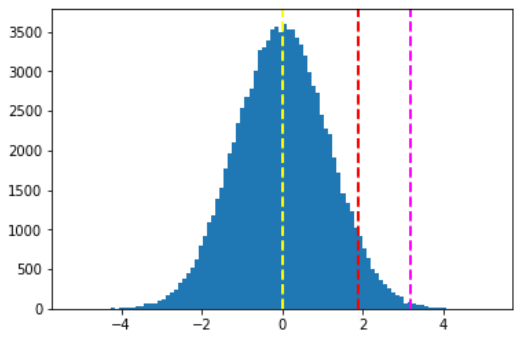

圖二. 假設檢定

統計誤差範圍計算

柯文哲講的統計誤差，嚴格上應稱為『抽樣誤差』(margin of error)，為信賴區間的一半，在顯著水準5%下即1.96σ，意思是如果調查結果介於(μ-1.96σ, μ+1.96σ)間，即圖一白色區域，落在此區間就有可能是抽樣產生的誤差，差異不顯著，相關說明可參閱『維基百科 Margin of error』或『什麼是抽樣誤差？老師和媒體都沒教你的那些事』。

一般民意調查若設定抽樣誤差(margin of error)為3%，那要調查多少人呢? 很簡單，依照抽樣誤差及標準誤差公式推算即可。

# 在顯著水準5%下，抽樣誤差 = 1.96 * 標準誤差(σ)
# 1.96 * σ = 0.03 (抽樣誤差)
# σ = (p * (1-p) / n) ** (1/2)
# ==> n = (p * (1-p)) * (σ ** 2)
n = 0.5 * 0.5 / ((0.03/1.96) ** 2)
print(n)

n=1067.1111111111109，因此，大部分的民調都設定有效樣本數為1068人，但拒答的人數無法預測，通常會多調查一些份數，因而每一份民調的有效樣本數會略有差異，參閱『2020年中華民國總統選舉民意調查 - 維基百科，自由的百科全書』：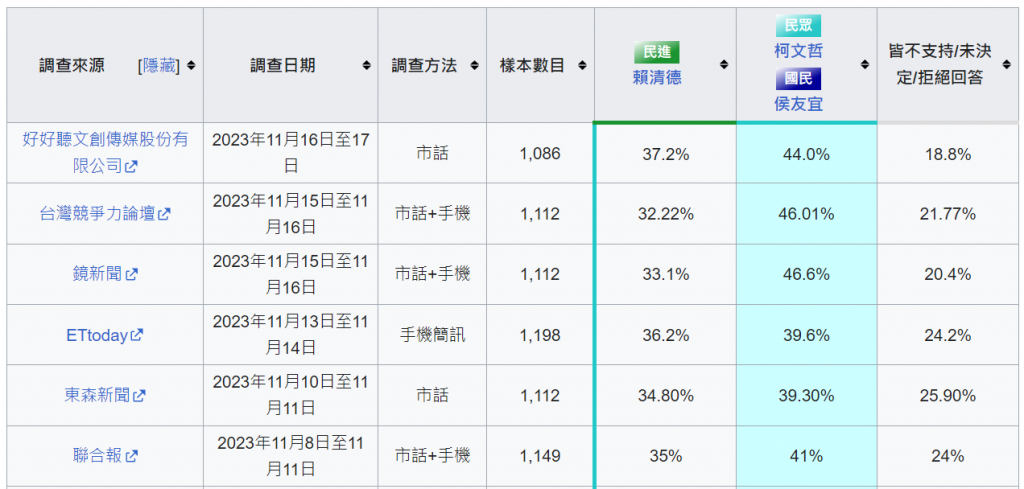

因為有效樣本數(n)不等，每一份民調計算出來的抽樣誤差也會有所差異，上表並未顯示，讀者可依公式計算，例如第一筆【好好聽文創傳媒股份有限公司】：

# 計算抽樣誤差
n=1086
std = 1.96 * ((0.5 * 0.5 / n) ** (1/2))
print(std)

抽樣誤差 = 0.02973795932268582，接近3%。

若調查的有效樣本(n)為2000份，則抽樣誤差為0.02191346617949794，即2.2%，計算如下：

# 計算抽樣誤差
n=2000
std = 1.96 * ((0.5 * 0.5 / n) ** (1/2))
print(std)

因此，柯文哲有時候講『讓3%』，有時候講『統計誤差範圍內』，算侯友宜贏，這兩種說法是不一致的，因為每一份民調的n都不一樣，抽樣誤差不會都等於3%，這是兩造的爭論點之一。

讀者如果只想知道抽樣誤差答案，不要寫程式，可以使用網頁計算器，也可以問ChatGPT，請參閱這則Yahoo新聞。

3%或6%

更大的爭論點是統計誤差範圍(即抽樣誤差)應該是3%或6%? 這也是說法不精準造成的結果，圖一為雙尾檢定(Two-tailed test)，但這場民調只關心『柯文哲是否顯著勝過侯友宜』，故應該只關心圖一右邊灰色區域，即民調統計量是否落入右邊灰色區域，也就是單尾檢定，應如下圖：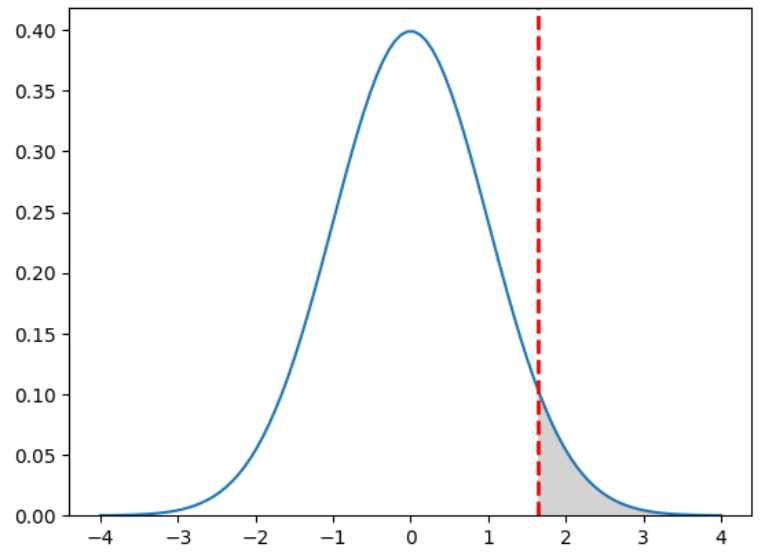

圖三. 單尾假設檢定

若『顯著水準』仍訂為5%，右邊灰色區域應加大為2倍，亦即紅線應為μ+1.645σ，驗證如下：

mean, std = 0, 1
# norm.cdf：常態分配的累積密度函數
Upper_bound = norm.cdf(mean + 1.645 * std, mean, std)
print(f'{Upper_bound:.3f}, {1 - Upper_bound:.3f}')

執行結果： 灰色區域機率總和為5%。

有人主張『抽樣誤差應該隨之加大為2倍，由3%擴大為6%』，這是錯誤的，因為1.645σ < 1.96σ，抽樣誤差反而變小，而民眾黨則堅持只讓3%，亦即『仍採用雙尾檢定，但只關心右邊灰色區域』，這與一般假設檢定作法也有所差異，如果採用雙尾檢定，假設應如下：
對立假設 H1：柯文哲支持度(μ1) ≠ 侯友宜支持度(μ2)
虛無假設 H0：柯文哲支持度(μ1) = 侯友宜支持度(μ2)

這又是表達不精準的問題，正確的講法應該是：
在5%顯著水準下進行單尾假設檢定，若民意調查結果柯文哲『顯著』勝過侯友宜，才算贏。
但一般民眾可能無法理解上述專業術語，建議可以改為：
以符合學理的民意調查方法下，柯文哲支持率領先侯友宜3%以上，才算贏。

結論

維基百科敘述：

19世紀英國首相班傑明·迪斯雷利曾說：『世界上有三種謊言：謊言，該死的謊言，統計數字』(Lies, damned lies, and statistics)。
統計數字由不同的人解讀，常會有截然不同的解釋，引用統計名詞時，務必要了解背後的理論基礎，精準描述問題及『假設』，不要隨意引用專業術語，不懂裝懂，只會自取其辱。

程式下載

相關程式可至這裡下載。

工商廣告:)

影音課程：

開發者必學：OpenAI API應用與開發。
ChatGPT企業實踐指南 | 技術透析與整合應用。
深度學習PyTorch入門到實戰應用。

書籍：

ChatGPT 完整解析：API 實測與企業應用實戰。
Scikit-learn 詳解與企業應用。
開發者傳授 PyTorch 秘笈
深度學習 -- 最佳入門邁向 AI 專題實戰。