前言

今年五月一篇論文【KAN: Kolmogorov-Arnold Networks】引發廣泛的討論，因為，它突破神經網路的框架，提出建構深度學習模型的另一種選擇，自1950年代以來，神經網路一直是建構深度學習模型的基礎，利用梯度下降法(Gradient descent)找到神經網路模型的最佳解，論文作者劉子鳴(Ziming Liu)創新思維，提出另一套演算法Kolmogorov-Arnold Networks，簡稱KAN，期望建構更好的深度學習模型。

神經網路與梯度下降法

在介紹KAN之前，先複習一下神經網路模型，神經網路係模擬生物神經傳導系統，藉由神經元傳導訊息，透過層層的分析與傳遞，最後傳到大腦，進行判斷，如下圖。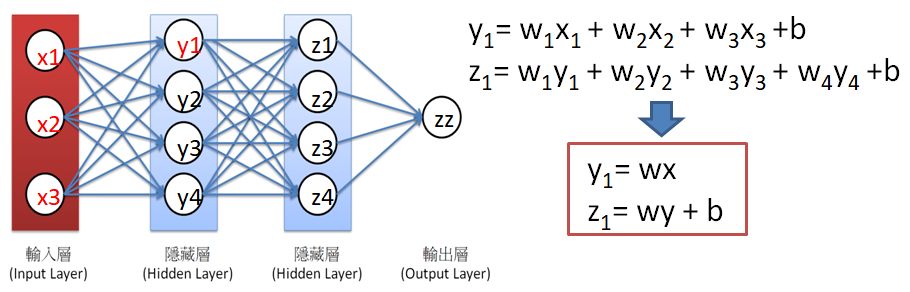

圖一. 生物神經傳導系統示意圖

學者將生物神經傳導系統簡化成神經網路(Neuron network)，如下圖，每個圓圈代表神經元，一個神經層擁有多個神經元，透過正向傳導(Forward propagation)，最後會到達輸出層，進行推論(Inference)，譬如辨識或生成。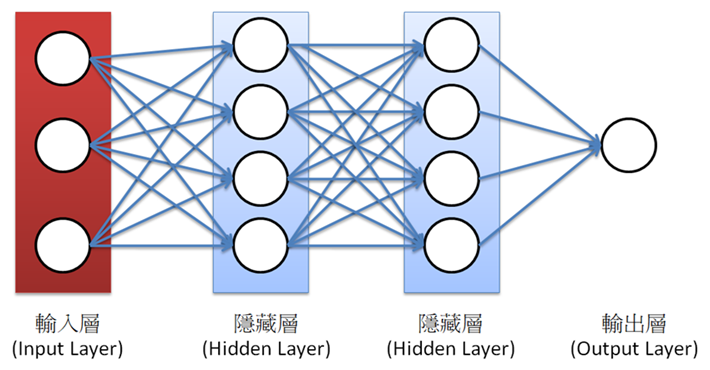

圖二. 神經網路(Neuron network)示意圖

若不考慮Activation Function，一個神經網路可視為多條迴歸(Regression)組合而成的模型，如下圖。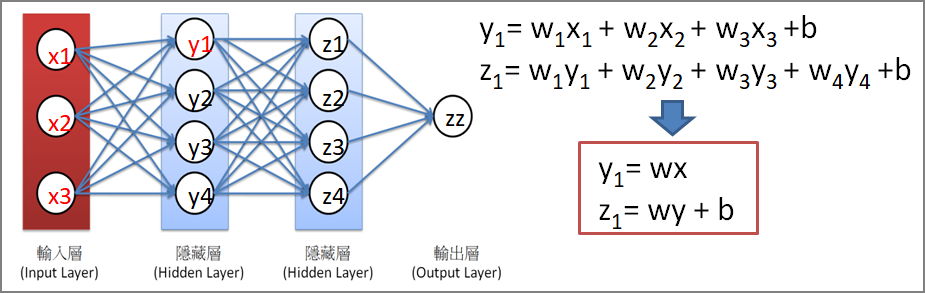

圖三. 簡化的神經網路

但簡化的神經網路只能產生線性模型，為達到最大通用性(Generalization)，學者加入Activation Function，將迴歸轉換為非線性函數，例如羅吉斯函數(Sigmoid)。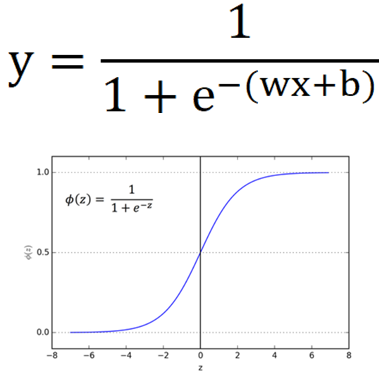

圖四. 羅吉斯函數(Sigmoid)

加入Activation Function後，要以數學求解神經網路就變的非常困難，因此，學者就提出優化法(Optimization)尋求近似解，其中最有名的演算法就是【梯度下降法】(Gradient descent)，運用正向/反向傳導反覆進行的方式，逐步逼近最佳解。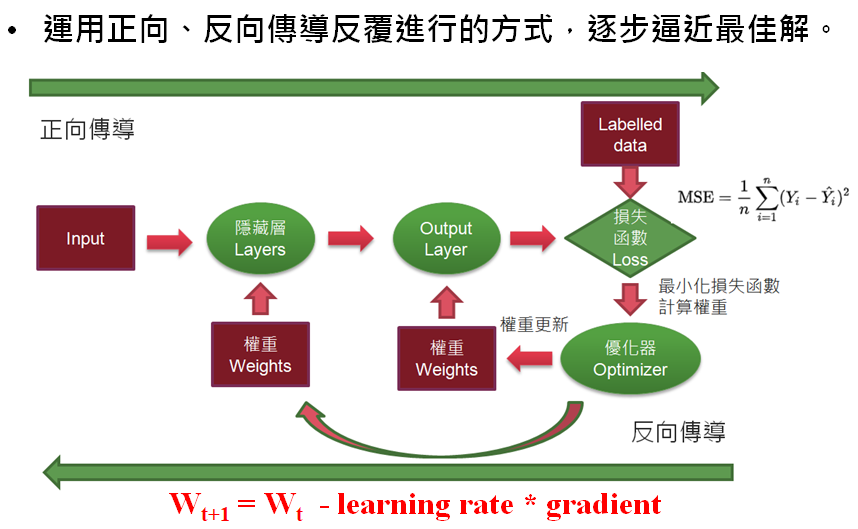

圖五. 梯度下降法(Gradient descent)

梯度下降法缺點

以上的機制有一個重大的缺點，建構神經網路時必須指定各個神經層後接何種Activation Function，例如圖六紅線標示，通常，隱藏層使用ReLU，輸出層使用SoftMax，事實上Activation Function有數十種，如何選用全憑經驗與實驗，也就是說，訓練模型前必須先固定Activation Function種類，因此，梯度下降法本質上還是在求解迴歸的參數--斜率(w)與偏差(b)。Activation Function種類可參閱維基百科，截取部分表格如圖七。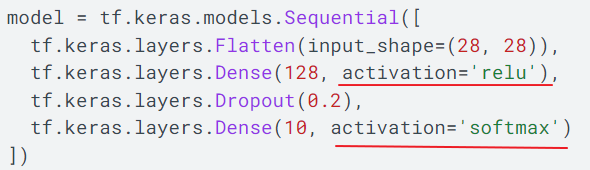

圖六. 神經網路模型建構的程式碼

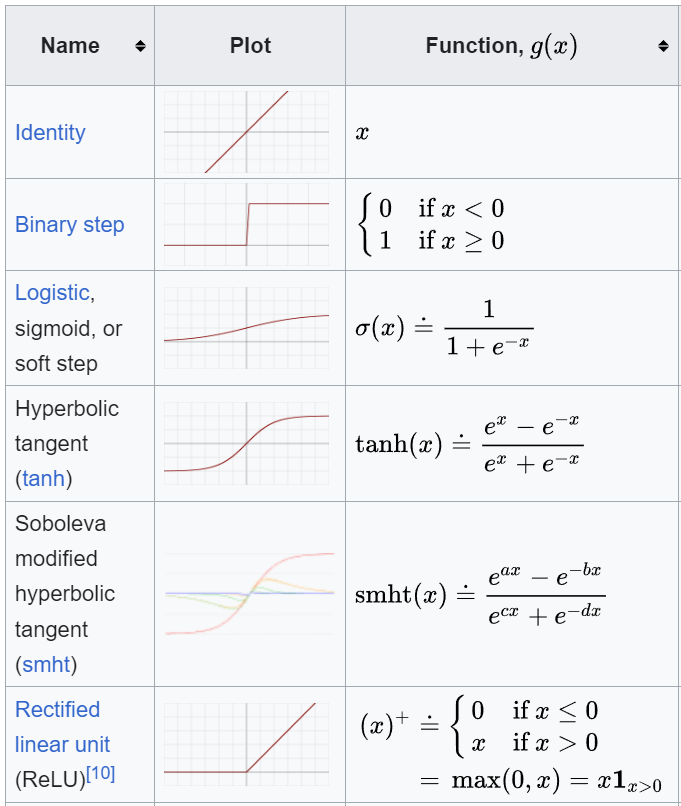
圖七. Activation Function 部分列表

Kolmogorov-Arnold Networks(KAN)

MIT博士生劉子鳴(Ziming Liu)為克服上述缺點，利用Kolmogorov-Arnold representation theorem定理，提出KAN解題方法，特點整理如下：

1. 不固定Activation Function，直接求解非線性函數。

2. 依據Kolmogorov-Arnold representation theorem，將多元方程式轉換為多個一元方程式組合，類似【傅立葉轉換】(Fourier Transform)。多元方程式轉換轉換為2n+1個一元方程式，如下：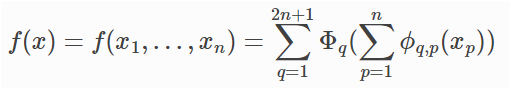
   

3. 一元方程式可使用 B-spline curve函數表示，B-spline curve可利用控制點(Control point)決定曲線形狀，因此，我們只要求解B-spline curve的控制點即可。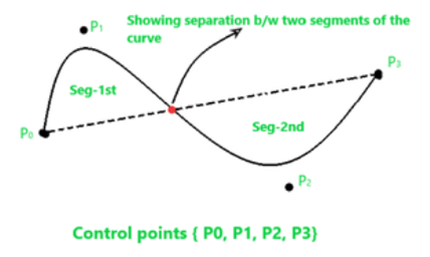
   
   圖八. B-spline curve與控制點(Control point)，圖片來源：B-Spline Curve in Computer Graphics
   

4. 沿用神經網路概念，可使用多個神經層，利用微分的連鎖律(Chain rule)，一次求得每一層的參數。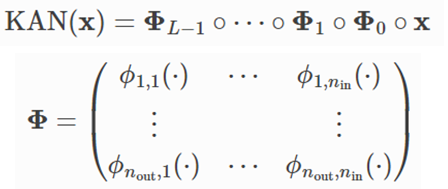
   

論文作者整理一張KAN與神經網路(MLP)的比較表，重點如下：

1. MLP是固定Activation Function，求解線性函數，KAN的Activation Function是透過訓練得到的(learnable)。
2. 其他概念是相通的，KAN吸取MLP的機制精華。

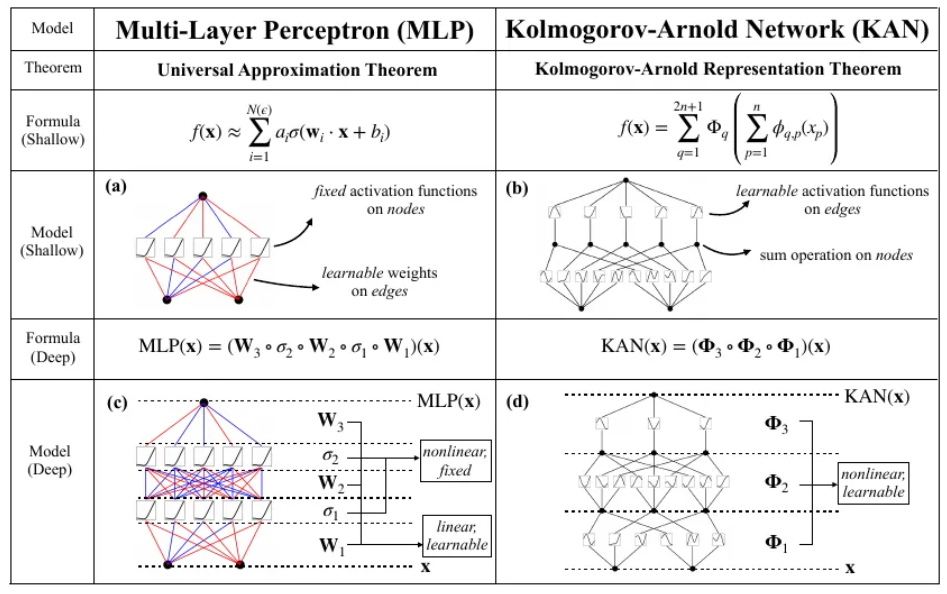
圖九. KAN與神經網路(MLP)的比較表

實作

作者不僅發表論文，也實作一個完整Python套件pykan及說明文件，真是太佛心了。

1. 安裝：pip install git+https://github.com/KindXiaoming/pykan.git ，範例中常會使用Scikit-learn、PyTorch，建議直接安裝Anaconda及PyTorch。
2. 範例：套件內有數十個範例程式，可供實驗，包括基礎的API呼叫範例(API_xx.ipynb)及機器學習範例(Example_xx.ipynb)。

針對Example_3_classfication.ipynb說明如下：

1. 引用套件。

from kan import KAN
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch
import numpy as np

2. 產生隨機的2類非線性分離的資料集。

dataset = {}
train_input, train_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)
test_input, test_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)

dataset['train_input'] = torch.from_numpy(train_input)
dataset['test_input'] = torch.from_numpy(test_input)
dataset['train_label'] = torch.from_numpy(train_label[:,None])
dataset['test_label'] = torch.from_numpy(test_label[:,None])

X = dataset['train_input']
y = dataset['train_label']
plt.scatter(X[:,0], X[:,1], c=y[:,0])

3. 執行結果：黃色及紫色2類資料。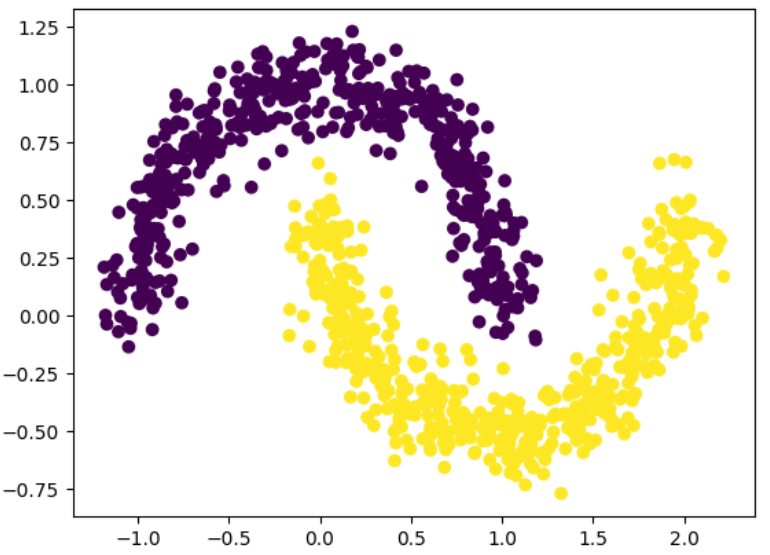
   

4. 建構KAN模型，參數width表各個神經層的神經元個數，grid表示一個多元方程式可由多個B-spline curve構成，稱之為【Grid extension】，如下圖，參數k=3為三次方的多項式。注意，原程式只寫 KAN()，筆者執行會出現錯誤，須改為KAN.KAN()，其他範例也須作同樣修正。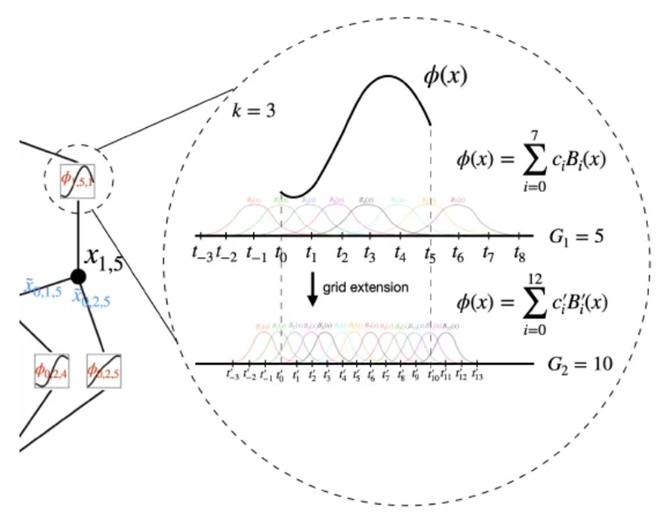
   

model = KAN.KAN(width=[2,1], grid=3, k=3)

5. 模型訓練：model.train。

def train_acc():
    return torch.mean((torch.round(model(dataset['train_input'])[:,0]) == dataset['train_label'][:,0]).float())

def test_acc():
    return torch.mean((torch.round(model(dataset['test_input'])[:,0]) == dataset['test_label'][:,0]).float())

results = model.train(dataset, opt="LBFGS", steps=20, metrics=(train_acc, test_acc));
results['train_acc'][-1], results['test_acc'][-1]

6. 執行結果：(0.9990000128746033, 0.9990000128746033)，訓練及測試資料準確率均約為0.99，針對非線性分離的資料集效果非常好。

7. 也可以自動或手動指定activation functions，以下為自動找出最佳activation functions，lib為各種activation functions。

lib = ['x','x^2','x^3','x^4','exp','log','sqrt','tanh','sin','tan','abs']
model.auto_symbolic(lib=lib)
formula = model.symbolic_formula()[0][0]
formula

8. 執行結果：經過訓練，最佳組合為第一個activation functions是sin，第二個activation functions是tan。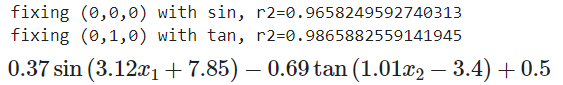
   

9. 最佳組合準確率測試：

def acc(formula, X, y):
    batch = X.shape[0]
    correct = 0
    for i in range(batch):
        correct += np.round(np.array(formula.subs('x_1', X[i,0]).subs('x_2', X[i,1])).astype(np.float64)) == y[i,0]
    return correct/batch

print('train acc of the formula:', acc(formula, dataset['train_input'], dataset['train_label']))
print('test acc of the formula:', acc(formula, dataset['test_input'], dataset['test_label']))

10. 執行結果：(0.9980, 0.9990)，效果也非常好。

結論

KAN特點是數學、準確與可解釋性，如下圖所示。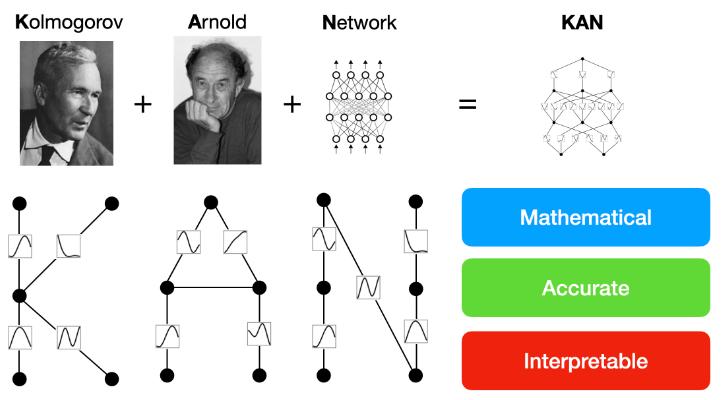

KAN與神經網路(MLP)比較，優點如下：

1. KAN訓練速度較快。
2. KAN要估計的參數量較少。
3. KAN求解收斂較快。

主要缺點：需遞迴估計 B-spline curve 參數，計算需要O(N²LG)，大於MLP的O(N²L)。但作者認為相對上KAN要估計的參數較少、求解收斂速度較快，可以克服上述缺點。

選擇 KAN的時機：

1. 資料較具結構性，例如聲波(Waveform)。
2. 希望是連續性的學習(Continual learning)：B-spline curve是連續型的函數，不是線性函數。
3. 高維(High dimensional)的資料集，顯然KAN較適用於深度學習，而非傳統的機器學習演算法。

目前範例多是傳統的機器學習，例如分類(Classification)或集群(Clustering)，缺少深度學習範例，較不能彰顯其優點，相信未來會有更多的深度學習範例出現。

另外，讀者應該會問，進階的演算法CNN、RNN，甚至最夯的Transformer如何實現呢? 其實CNN、RNN都是特徵的萃取，例如Convolution只是將像素轉換為線條或輪廓而已，原則上，應該可以與KAN介接，KAN只是對應完全連接層(Full-connected layer)而已。

在一片生成式AI討論聲中，很高興看到KAN的出現，換一換口味。