回顧一下昨天介紹的內容，我們了解 TF-IDF 可以用來計算一個單詞在這篇文章中的重要程度，通過以下兩個指標：

• TF = ( 單詞在文檔中出現的次數 ) / ( 文檔中的總單詞數 )
• IDF = ( 文檔總數 ) / ( 包含該單詞的文檔數 )

兩者相乘就可以得到這個單詞的 TF-IDF 值，那麼今天就來把進階和實作的部分講完吧。

修改 TF 公式

為什麼要修改 TF 的計算方式呢？因為我們發現它存在著一些缺陷，舉例來說：

doc1：This is a dog. The dog is cute.
doc2：This is a dog. This is a cat.

經由計算後得知：

TF("dog", doc1) = 2 / 8
TF("cat", doc1) = 0 / 8
TF("dog", doc2) = 1 / 8
TF("cat", doc2) = 1 / 8

當使用者想要查詢和 dog、cat 都有關的文章時，卻會發現 doc1 和 doc2 的 TF 值相同，而明明 doc2 才是更接近使用者想要搜尋到的文章。

為了抑制某一個單詞出現太多次導致 TF 值過高的問題，我們將公式修改成這樣：

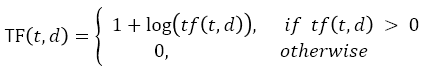
tf(t, d) 就是原本計算出來的 TF 值，我們把它加上 log 之後，在單詞出現頻率很高的情況下，分數會受到抑制。從下面這張圖可以更明顯地看出來公式修正前後的差別：

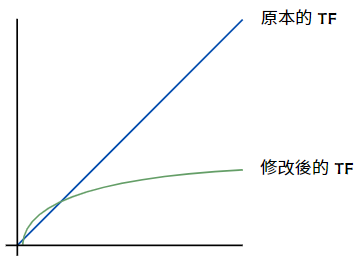
現在用修正後的公式再把剛剛那個情況計算一遍：

TF("dog", doc1) = 1.3
TF("cat", doc1) = 0
TF("dog", doc2) = 1
TF("cat", doc2) = 1

加總之後，doc1 的 TF 值變成 1.3，而 doc2 的 TF 值維持 2，這樣就達到我們修改的目的了。

當然，TF 的公式因為需求和使用場景不同，也產生很多不同的變形，大家有興趣可以去查查。

修改 IDF 公式

接下來是 IDF 修正後的公式：

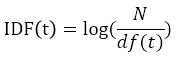
N 代表文檔總數，df 代表包含該單詞的文檔數，所以 IDF 的修正公式就只是對原本的 idf 值加上一個 log 而已。

這樣做的好處是可以把 IDF 的規模縮小，舉個例子來說：

假設所有的文檔共有一億個 ( N = 10^8 )，但某個單詞就只有出現在其中一篇文章而已，按照原本的計算方式 IDF 值就會是 100000000，然而加上 log 之後，新的 IDF 值瞬間縮小到只有 8。

這個想法其實和 TF 的修正公式一樣，都是要避免線性成長造成數值可能過大的問題。

此外，如果某一個單詞在所有文檔中都出現過一次，代表它的重要性非常低，加上 log 後 IDF 就會是 0 而不是 1，也代表整個 TF-IDF 值也是 0，與 TF 值沒有關係。

IDF 也有很多變形公式，大家有興趣也可以去查查看。

所以最終的 TF-IDF 公式就會是下面這樣：

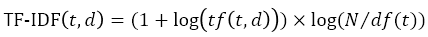
接下來就進入實作吧！

我們可以直接使用 Sklearn 提供的 TfidfVectorizer 工具，不過就像剛剛提到的，不同情境下使用的公式也有所不同，所以執行的結果未必就會就和我們計算的結果相同：

from sklearn.feature_extraction.text import TfidfVectorizer
import pandas as pd

documents = ["The weather is great today", "I am feeling happy today", "I am not feeling well today"]

vectorizer = TfidfVectorizer()
tfidf_matrix = vectorizer.fit_transform(documents)
feature_names = vectorizer.get_feature_names_out()

df = pd.DataFrame(tfidf_matrix.toarray(), columns = feature_names)
df.index = [f"Document {i+1} " for i in range(len(documents))]
print(df)

首先把所有的單詞和文章列出來，然後用矩陣的方式顯示對應的 TF-IDF 值，觀察輸出結果可以發現，I 被當作 stopword 刪除了，此外，在三篇文章中都有出現的 today 確實分數被抑制了，並且關鍵訊息 happy、not well 都有被凸顯出來。

不過這個例子中的文檔數量還是太少，如果是對好幾萬份文章做處理的話，效果會更明顯。

明天我們會進入到 BM25 的主題，它是由 TF-IDF 發展而來，是執行非常快速而且效果還不錯的檢索方式，我們會分兩個部分來介紹，一樣是先分析公式，最後再實作看看。

推薦文章
dapi2021-information-retrieval (up.pt)
Understanding TF-IDF and BM-25 - KMW Technology (kmwllc.com)