單純貝氏分類器（Naive Bayes classifier）

一種貝葉斯定理簡單概率分類器。假設每個特徵都是相互獨立的，並且可以同時接受離散型變數和連續型變數

訓練過程

• 計算每個特徵類別中先驗概率
• 計算每個特徵類別中後驗概率

貝氏定理公式

計算先驗概率

先驗概率是指在沒有任何其他信息的情況下，一個事件發生的概率。在單純貝氏分類器中，先驗概率可以通過計算每個類別在訓練數據中的比例來估計

例如

• 訓練數據中有60%數據屬於類別 A
• 40%數據屬於類別 B
• 類別 A 先驗概率為 0.6
• 類別 B 先驗概率為 0.4

計算後驗概率

後驗概率是指在已知其他信息的情況下，一個事件發生的概率。在單純貝氏分類器中，後驗概率可以通過應用貝葉斯定理來計算。

P(A | B) = P(B | A) * P(A) / P(B)

• P(A | B) 已知 B 發生下，A 發生概率
• P(B | A) 已知 A 發生下，B 發生概率
• P(A) A發生先驗概率
• P(B) B發生先驗概率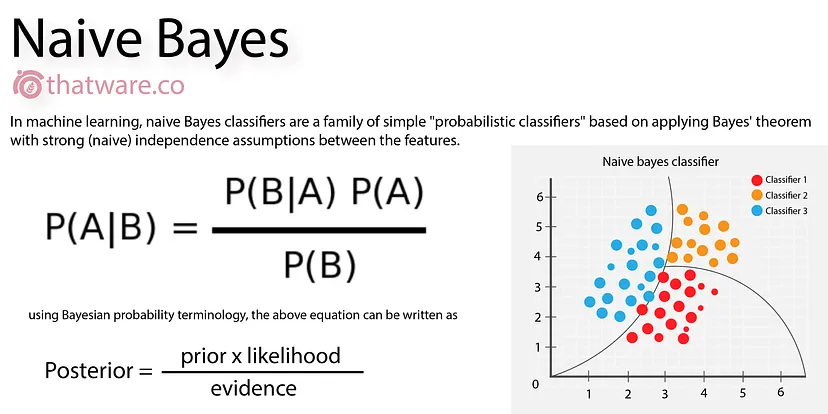
  
  圖片來源:(https://towardsdatascience.com/introduction-to-na%C3%AFve-bayes-classifier-fa59e3e24aaf)

單純貝氏分類

在單純貝氏分類器中，P(B | A) 可以通過計算每個特徵在每個類別中條件概率來估計
條件概率是指在已知一個事件發生下，另一個事件發生的概率

例如

• 假設在類別 A 中，特徵 X 的值為 x 的概率為 0.8
• 在已知類別為 A 的情況下，特徵 X 的值為 x 的條件概率為 0.8

將先驗概率和條件概率代入貝葉斯定理，可以得到後驗概率：
P(A | X = x) = P(X = x | A) * P(A) / P(X = x)

• P(A | X = x) 已知特徵 X 的值為 x 下，類別 A 發生的後驗概率
• P(X = x | A) 已知類別 A 的情況下，特徵 X 的值為 x 的條件概率
• P(A) 類別 A 先驗概率
• P(X = x) 特徵 X 的值為 x 邊緣概率

在分類階段，單純貝氏分類器會根據驗概率來對新數據進行分類。新數據將被分配到具有最大後驗概率的類別

例如

• 假設一個新數據的特徵 X 的值為 x

• 根據上述計算，可以得到類別A和類別B後驗概率：
  P(A | X = x) = 0.8 * 0.6 / P(X = x)
P(B | X = x) = 0.2 * 0.4 / P(X = x)

• 如果 P(A | X = x) > P(B | X = x)

  • 新數據將被分配到類別A
  • 否則，新數據將被分配到類別B

單純貝氏優缺點

應用

• 文本分類
• 垃圾郵件檢測
• 欺詐檢測
• 醫學診斷

單純貝氏程式碼(Python-Scikit-learn)

from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 假設我們已經準備好訓練數據 X 和標籤 y
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 創建一個高斯樸素貝葉斯分類器
gnb = GaussianNB()

# 訓練模型
gnb.fit(X_train, y_train)

# 進行預測
y_pred = gnb.predict(X_test)

# 計算準確度
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

結論

單純貝氏分類器是一種簡單有效的分類器，具有廣泛的應用前景。然而，在實際應用中，需要考慮其優缺點，並根據具體情況進行調整