階層式分群 (Hierarchical Clustering)

是一種常見的聚類分析方法，透過建立一個樹狀結構（樹狀圖），將資料點逐層合併或分裂成不同的群組。這個樹狀結構直觀地展示了資料點之間的相似性，以及群組之間的層次關係

階層式分群類型

凝聚式分群 (Agglomerative Clustering)

由下而上，一開始將每個資料點視為一個群組，然後逐步合併距離最近的兩個群組，直到所有資料點都屬於同一個群組

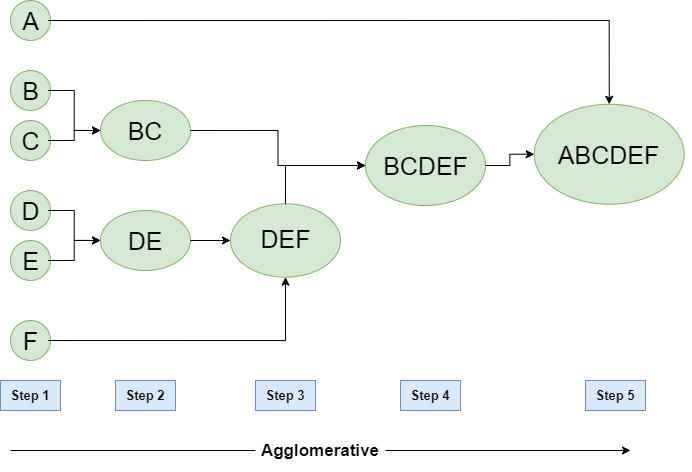
圖片來源:Hierarchical Clustering in Machine Learning

分裂式分群 (Divisive Clustering)

由上而下，一開始將所有資料點視為一個群組，然後逐步將群組分裂成兩個子群組，直到每個資料點都成為一個獨立的群組

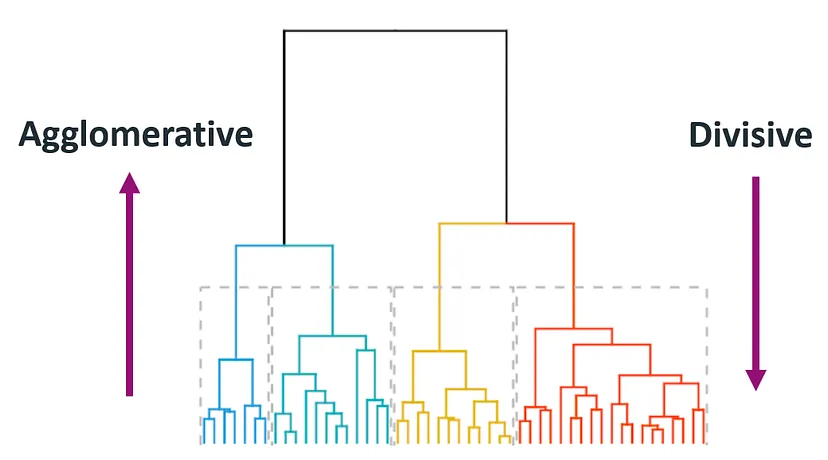
圖片來源:Hierarchical Clustering in Machine Learning

階層式分群流程 (凝聚式分群為例)

1. 初始化：將每個資料點視為一個獨立的群組
2. 計算距離：計算所有群組之間的距離
3. 合併：選擇距離最近的兩個群組進行合併
4. 更新：更新群組之間的距離矩陣
5. 重複步驟2-4：直到所有資料點都屬於同一個群組

距離測量

• 歐式距離 (Euclidean Distance):最常用的距離測量方法，用連續型資料
• 曼哈頓距離 (Manhattan Distance):計算兩個點在座標軸上的絕對差之和
• 閔可夫斯基距離 (Minkowski Distance):歐式距離和曼哈頓距離的推廣
• 餘弦相似度 (Cosine Similarity):測量兩個向量之間的相似性，常用文本分析

計算距離矩陣(Distance Matrix)

在階層式分群 (Hierarchical Clustering) 中，合併兩個群時，會檢查每對群之間的距離，並合併距離最小或相似度最高的群。但問題是如何定義群間距離或相似度

距離測量方法

• 最小距離(Min Distance):找到兩個群中任意兩點之間的最小距離
• 最大距離(Max Distance):找到兩個群中任意兩點之間的最大距離
• 群平均(Group Average):找到兩個群中每兩點之間距離的平均值
• Ward's method:將兩個群組合併時，選擇能使組內平方和增加最小的合併方式

圖片來源:Hierarchical Clustering in Machine Learning

連接方式 (Linkage)

• 單鏈接法 (Single Linkage):兩個群組中最接近的兩個點之間的距離
• 完全鏈接法 (Complete Linkage):兩個群組中最遠的兩個點之間的距離
• 平均鏈接法 (Average Linkage):兩個群組中所有點對之間距離的平均值
• Ward's method:將兩個群組合併時，選擇能使組內平方和增加最小的合併方式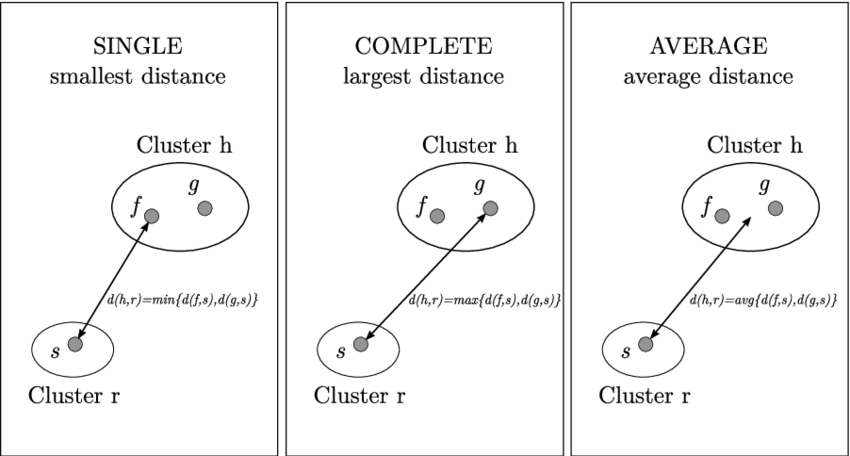

圖片來源:Hierarchical Clustering in Machine Learning

公式 (Ward's method)

Ward's method 目標是找到合併兩個群後，使得群內平方和增量最小。假設有兩個群 A 和 B，合併後的群為 C，則 Ward's method 的目標是：

minimize: ∑(x_i - c)^2, where x_i ∈ C, c is the centroid of C

樹狀圖 (Dendrogram)

是階層式分群的視覺化結果，水平軸表示資料點，垂直軸表示距離。樹狀圖的枝條代表合併的過程，枝條的高度表示合併時的距離

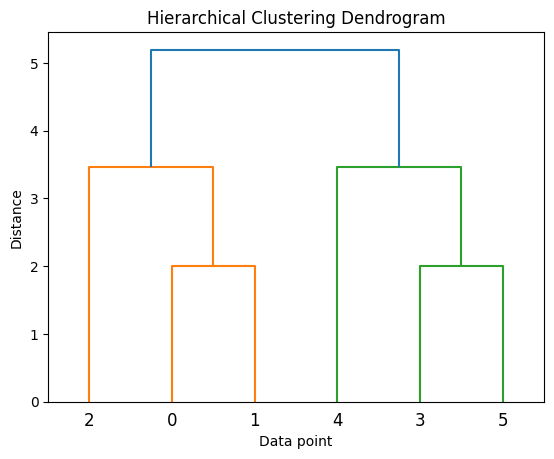
圖片來源:Hierarchical Clustering in Machine Learning

階層式分群優缺點

優點

• 不需要事先指定群組數量
• 可以產生具有層次結構的結果
• 可以處理任意形狀的資料

缺點

• 計算複雜度高，不適合大規模資料
• 對噪聲敏感
• 選擇合適的距離測量和連接方式需要經驗

應用

• 生物學：基因分類、蛋白質結構分析
• 市場營銷：客戶分群、產品分類
• 圖像處理：圖像分割
• 社會科學：社群分析

注意事項

階層式分群的結果對距離測量和連接方式的選擇非常敏感
選擇合適的群組數量需要根據具體問題和領域知識進行判斷
可以結合其他聚類方法和視覺化技術來驗證聚類結果

程式碼範例 (Python-Scikit-learn)

from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
import numpy as np

# 生成隨機資料
X = np.random.rand(150, 2)

# 建立聚類模型
clustering = AgglomerativeClustering(n_clusters=3, linkage='ward')

# 進行聚類
clustering.fit(X)

# 視覺化結果
plt.scatter(X[:, 0], X[:, 1], c=clustering.labels_)
plt.show()

總結

階層式分群是一種強大的聚類方法，能提供資料點之間的層次關係。但計算複雜度高，對於大數據集可能不太適合。在選擇階層式分群時，需要考慮資料的特性、距離測量方法以及聚合或分裂的方式