邏輯迴歸(Logistic Regression)

是一種統計學方法，估計一個或多個自變數與一個二元應變數之間的關係。也是一種廣泛使用的分類建模技術，在許多領域都有應用，包括工程、經濟學、金融、生物學和社會科學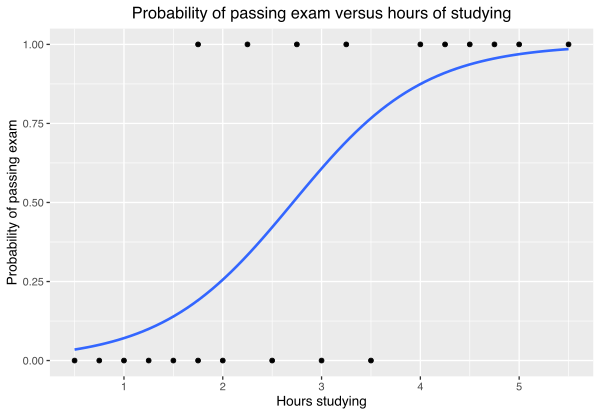

圖片來源:Logistic regression

邏輯迴歸模型

邏輯迴歸模型假設應變數是二元的，並且其取值概率可以表示為自變數的線性組合的函數。常用的函數是 邏輯函數 (sigmoid function)，也稱為 S 形曲線

f(x) = 1 / (1 + exp(-x))

x是自變數的線性組合

決策邊界

邏輯迴歸可以產生一個決策邊界，將特徵空間分成兩部分，分別對應於兩個類別

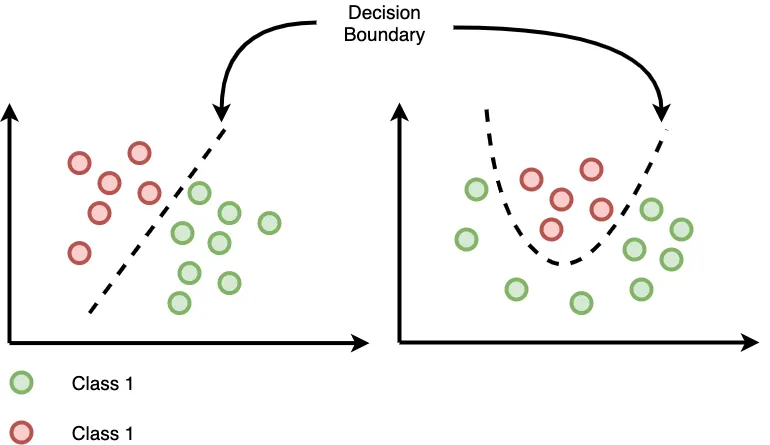
圖片來源:Logistic Regression and Decision Boundary

邏輯迴歸公式

線性組合

z = w0 + w1*x1 + w2*x2 + ... + wn*xn

Sigmoid函數

p(y=1|x) = σ(z) = 1 / (1 + exp(-z))

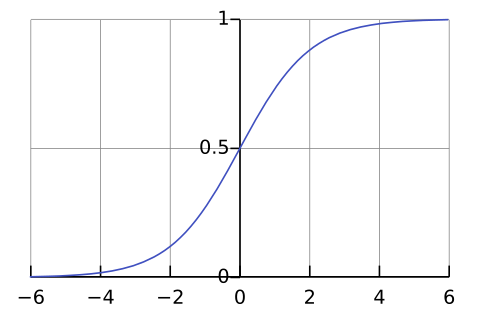
圖片來源:Sigmoid function

邏輯迴歸擬合

是找到一組參數，使得模型預測的概率與觀測資料的實際取值 максимально一致。常用擬合方法是 最大似然法 (MLE)

MLE是一種透過最大化似然函數來找到最佳參數方法

L(β) = ∏[f(xi)]^yi * [1 - f(xi)]^(1-yi)

邏輯迴歸評估

• 準確率：表示模型正確預測比例
• 召回率：表示模型正確識別正例比例
• F1分數：準確率和召回率調和平均值

邏輯迴歸應用

• 分類：分類垃圾郵件、預測客戶是否會違約或診斷疾病
• 預測：預測某人是否會投票給某位候選人或某支球隊是否會贏得比賽

邏輯迴歸限制

• 線性關係假設：邏輯迴歸假設自變數與應變數之間的關係是線性的。如果實際關係是非線性的，則邏輯迴歸模型可能不準確。
• 多重共線性：如果自變數之間存在多重共線性，則邏輯迴歸模型的參數估計可能會不穩定

邏輯迴歸擴展

• 多重邏輯迴歸：允許多個自變數
• 非線性邏輯迴歸：允許非線性關係
• 廣義線性模型(GLM)：允許非正態分佈的誤差項

邏輯迴歸程式碼(Python-Scikit-learn)

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 假設 X 是特徵矩陣，y 是目標向量

# 分割資料集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 建立模型
model = LogisticRegression()

# 訓練模型
model.fit(X_train, y_train)

# 進行預測
y_pred = model.predict(X_test)

# 評估模型
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

結論

邏輯迴歸是一種簡單但有效的統計學方法，在許多領域都有應用。然而，邏輯迴歸也有一些限制。在使用邏輯迴歸時，需要了解其限制並進行相應的處理