高斯混合模型 (Gaussian Mixture Model, GMM)

是一種概率分布模型，假設所有數據都是由多個高斯分布（常態分布）混合生成的。換句話說，將複雜的數據分佈分解成幾個簡單的高斯分布的加權和。這使得我們能夠更靈活地建模各種形狀的數據分佈。

想像一下，我們有一堆數據點，它們看起來不是簡單的鐘形曲線，而是由幾個不同中心和寬度的鐘形曲線疊加而成。GMM作用就是找到這些隱藏的鐘形曲線，並估計它們的參數（如均值、方差和混合權重）

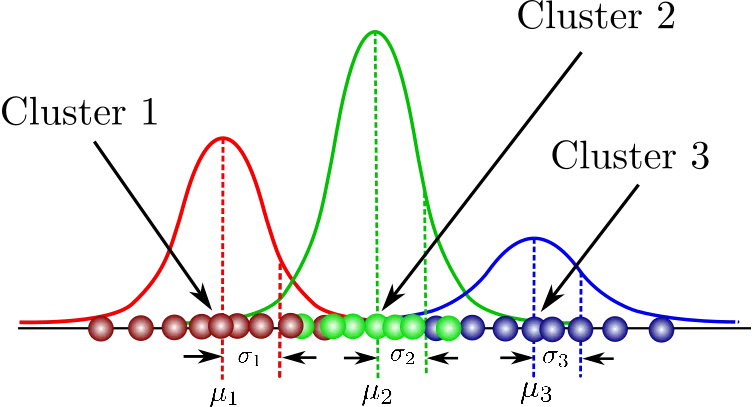
圖片來源:Gaussian Mixture Models Explained

GMM公式

p(x) = ∑(k=1 to K) π_k * N(x|μ_k, Σ_k)

N(x|μ_k Σ_k) 以 μ_k 為均值，Σ_k 為協方差矩陣的 k-th 高斯分布

GMM應用

• 語音識別：建模音素的概率分布
• 圖像分割：將圖像分割成不同的區域
• 異常檢測：檢測數據中的異常點
• 生物信息學：分析基因表達數據

GMM學習算法

• 期望最大化(EM)算法：EM算法是一種迭代算法，估計 GMM 的參數
• E步：計算每個數據點屬於每個高斯分布的概率
• M步：更新每個高斯分布的參數，使得似然函數最大化

GMM程式碼(Python-Scikit-learn)

from sklearn.mixture import GaussianMixture
import numpy as np

# 生成一些示例數據
X = np.concatenate((np.random.randn(100, 2), 4 * np.random.randn(300, 2)))

# 創建一個 GMM 模型，指定有 2 個混合成分
gmm = GaussianMixture(n_components=2)

# 訓練模型
gmm.fit(X)

# 预测新的数据点屬於哪個成分
labels = gmm.predict(X)

from sklearn.mixture import GaussianMixture
import numpy as np

# 生成一些示例數據
X = np.concatenate([
    np.random.randn(100, 2) + np.array([0, -2]),
    np.random.randn(300, 2) + np.array([2, 2])
])

# 創建 GMM 模型並進行擬合
gmm = GaussianMixture(n_components=2)
gmm.fit(X)

# 獲取模型參數
print(gmm.means_)  # 均值
print(gmm.covariances_)  # 協方差矩陣
print(gmm.weights_)  # 混合係數

總結

高斯混合模型是一種強大的概率模型，它可以有效地建模複雜的數據分佈。通過 EM 算法，我們可以學習 GMM 的參數。GMM 在機器學習、數據挖掘等領域有廣泛的應用