集群分析(K-means Clustering)

一種非監督式機器學習算法，將數據集劃分為預定義數量集群。目標是將彼此相似數據點歸為一類，與其他集群中數據點不同

K-means聚類優缺點

優點

• 簡單易懂，實現方便
• 計算效率高，適合大規模數據集
• 能夠發現球形簇

缺點

• 需要預先指定簇的數量K
• 對初始簇中心的選擇敏感
• 只能發現凸形簇
• 對噪聲和異常值敏感

K-means聚類應用

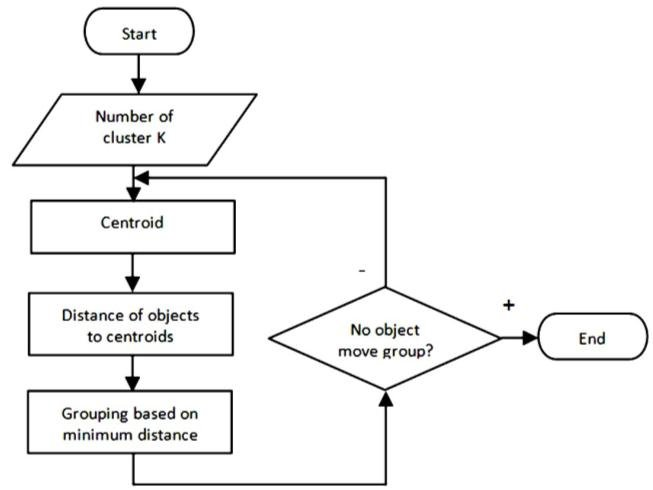
圖片來源:(https://www.researchgate.net/figure/K-means-clustering-process-flowchart_fig7_271305580)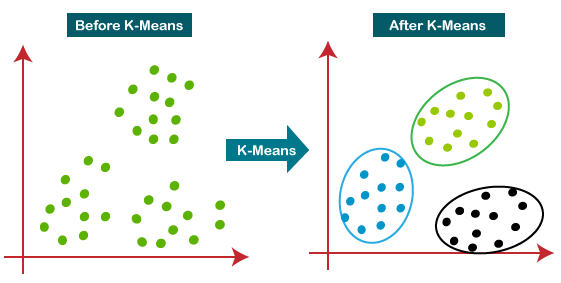

圖片來源:K Means Clustering in Python | Step-by-Step Tutorials for Clustering in Data Analysis

K-means聚類公式

數學公式

通常使用歐式距離來計算數據點與簇中心的距離

歐式距離

(x, c) = sqrt(Σ(xi - ci)^2)

對於兩個數據點 x 和 y，它們之間的歐式距離為：
distance(x, y) = sqrt(Σ(xi - yi)^2)

簇中心更新

ci = (1/ni) * Σ(x)
μ_i = (1/n_i) * Σ(x_j)

K-means程式碼(Python-Scikit-learn)

from sklearn.cluster import KMeans
import numpy as np

# 隨機生成一些數據
X = np.random.rand(100, 2)

# 創建 KMeans 模型，指定簇的數量
kmeans = KMeans(n_clusters=3, random_state=0)

# 訓練模型
kmeans.fit(X)

# 預測每個數據點屬於哪個簇
y_pred = kmeans.predict(X)

# 獲取簇中心
centers = kmeans.cluster_centers_

如何選擇最佳K值？

肘部法(Elbow Method)：繪製不同 K 值下的誤差平方和(SSE)，選擇SSE變化率下降最快的K 值
輪廓係數 (Silhouette Coefficient)：計算每個數據點的輪廓係數，選擇輪廓係數最高的K值
Gap Statistic： 比較數據集的聚類結果與隨機數據的聚類結果，選擇差異最大的K值

總結

K-means 聚類是一種強大聚類算法，但也有局限性在實際應用中，需要根據數據特點和具體需求選擇合適聚類算法