100. Same Tree

题目描述：

給定兩個二元樹的根節點 p 和 q，編寫一個函數來檢查它們是否相同。如果這兩棵樹在結構上完全相同，並且所有對應的節點的值都相同，則返回 true，否則返回 false。

Example 1: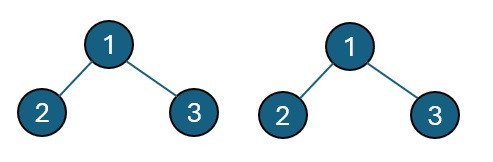

• Input: p = [1,2,3], q = [1,2,3]
• Output: true

Example 2:

• Input: p = [1,2], q = [1,null,2]
• Output: false

解題思路:
這道題目是關於二元樹的實作題，有兩種常見的解法：遞迴法和迭代法。我們先介紹比較直觀的遞迴法來解決這個問題。

遞迴法的思路是逐步比較兩棵樹的根節點及其子節點。如果兩個節點的值相同，並且它們的左右子樹也分別相同，那麼我們可以認為這兩棵樹是相同的。具體步驟如下：

1. 檢查根節點：首先，我們要檢查兩棵樹的根節點。如果兩個根節點都為 null，那麼它們是相同的，可以直接返回 true。
2. 處理空節點的情況：如果其中一棵樹的根節點是 null，而另一棵樹的根節點不是 null，那麼這兩棵樹肯定不同，直接返回 false。
3. 比較節點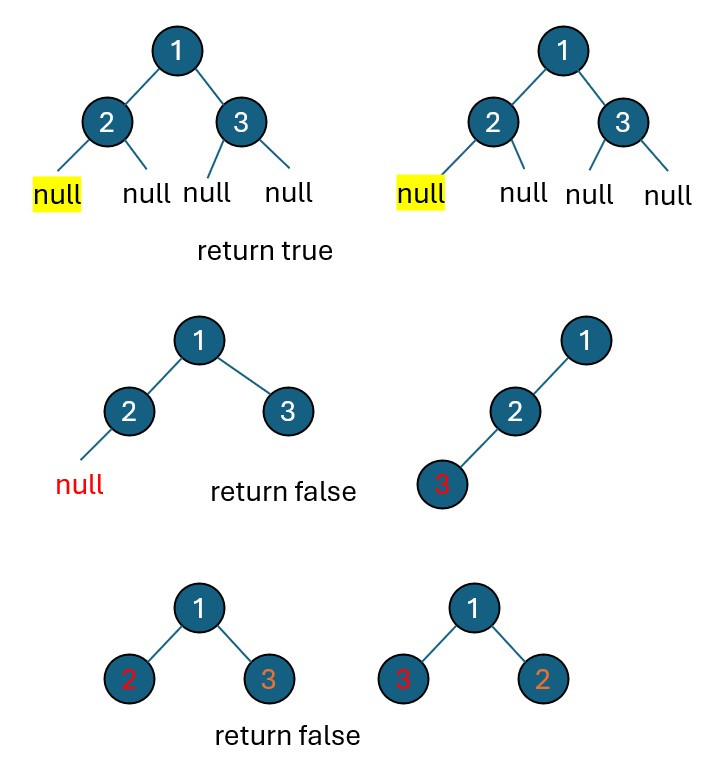的值：如果兩個根節點的值相等，我們需要進一步遞迴比較它們的左右子樹，確保左右子樹也都是相同的。如果兩者的值不相等，則直接返回 false。
   

var isSameTree = function(p, q) {
    if (!p && !q) return true;
    if (!p || !q) return false;
    if (p.val !== q.val) return false;

    return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};

時間複雜度：O(n)，其中 n 是樹中的節點數量。每個節點都會被訪問一次。
空間複雜度：O(h)，其中 h 是樹的高度。遞迴調用call stack的空間取決於樹的高度。

迭代法的思路其實和遞迴法相似，只是將遞迴過程轉換為使用 stack 來同時遍歷兩棵樹，逐一比較相應的節點。如果每個對應的節點都相同，那麼這兩棵樹就是相同的。

具體步驟如下：

1. 初始化 stack：首先，將兩棵樹的根節點都 push 到 stack 中。
2. 逐一比較節點：接著，我們開始從 stack 中取出節點進行比較。如果兩個節點的值相同，則需要繼續比較它們的子節點。
3. 處理左右子樹：如果兩個根節點的值相等，我們將這兩個節點的左右子樹分別 push 到 stack 中，然後繼續迴圈比較。
4. 重複過程：這個過程會不斷重複，直到 stack 為空。只要在這個過程中所有對應的節點都相同，我們就可以判斷這兩棵樹是相同的。

var isSameTree = function(p, q) {
    const stack = [[p, q]];

    while (stack.length > 0) {
        const [node1, node2] = stack.pop();

        if (!node1 && !node2) continue;
        if (!node1 || !node2) return false;
        if (node1.val !== node2.val) return false;

        stack.push([node1.left, node2.left]);
        stack.push([node1.right, node2.right]);
    }

    return true;
};

時間複雜度：O(n)，其中 n 是樹中的節點數量。每個節點都會被訪問一次。
空間複雜度：O(h)，其中 h 是樹的高度。遞迴調用stack的空間取決於樹的高度。

總結:
在這道題目中，我們使用了遞迴法和迭代法這兩種方式來比較二元樹，故歸類為「recursion」和「stack」這兩個分類。雖然這兩種方法的邏輯看似相同，但在實際應用中仍有一些差異。

遞迴法通過不斷地調用自身來處理每個節點，這會導致系統的call stack逐漸累積。如果樹的高度較大，這種方法可能會導致 stack overflow 問題。然而，遞迴法的代碼通常更簡潔且容易理解，特別是對於初學者來說。

迭代法則使用一個 while 迴圈和一個 stack 來模擬遞迴過程。雖然這樣做可以避免遞迴的深度限制問題，但會使代碼變得更加複雜。這種方法的優點是，它不會積累過多的call stack，並且更容易控制流程。

事實上，幾乎所有的遞迴方法都可以轉換為迭代方法，但這個轉換過程可能會讓代碼變得更加繁瑣和難以理解。因此，選擇使用遞迴法還是迭代法，應根據具體情況和需求來決定。如果問題的規模較小且不會導致stack overflow，遞迴法是個不錯的選擇；如果需要處理更大的數據或更深的樹，迭代法則更為合適。