資料來源：GrandmaCan -我阿嬤都會教學影片

機器如何學習?

• 機器學習 = 從資料中找出規則
• 深度學習 = 機器學習中的一種，模仿大腦中的類神經網路
• 機器如何學習？數學搭配程式(模型Model)
• 特徵(Feature)、標籤(Label)：
  以房屋的售價舉例，如果坪數對應到不同的售價，坪數為特徵(Feature)，而售價為 標籤(Label)，可以把特徵(Feature)、標籤(Label)輸入到模型中，不斷的修正後，訓練模型完成後，就可以將坪數輸入來評估價格，當然，特徵(Feature)可以有多種，像是地點、規格等等，讓模型進行訓練。

<簡單線性回歸 Simple Linear Regression>
任務：用年資預測薪水

1. 檔案輸入

import pandas as pd
url = "https://raw.githubusercontent.com/GrandmaCan/ML/main/Resgression/Salary_Data.csv"
data = pd.read_csv(url)
data

2. 分離資料

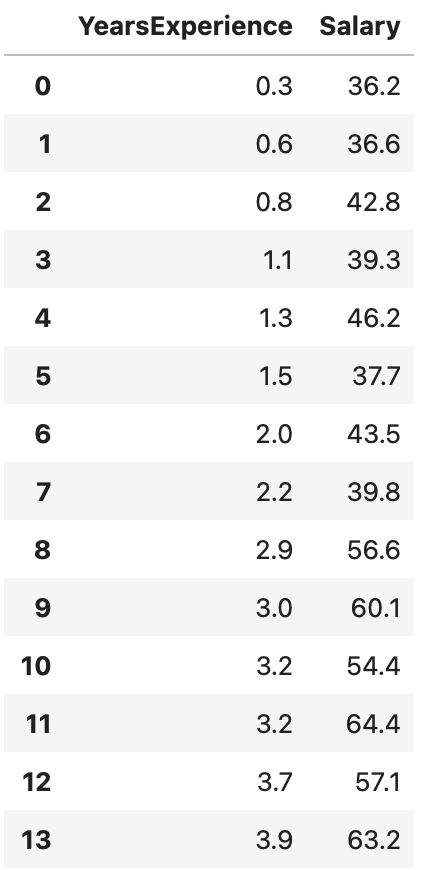
x = data["YearsExperience"]
y = data["Salary"]

3. 使用matplotlib畫出資料對應的圖
   python不支援中文字：可以先下載wget來下載文字字型

pip install wget
import wget
wget.download("https://github.com/GrandmaCan/ML/raw/main/Resgression/ChineseFont.ttf")
import matplotlib as mpl
from matplotlib.font_manager import fontManager
fontManager.addfont("Chinesefont.ttf")
＃設定字體
mpl.rc("font", family = "Chinesefont")

畫圖：

import matplotlib.pyplot as plt
plt.scatter(x, y, marker = "x", color = "r")
plt.title("薪水-年資“)

4. 畫出y = w．x + b的直線

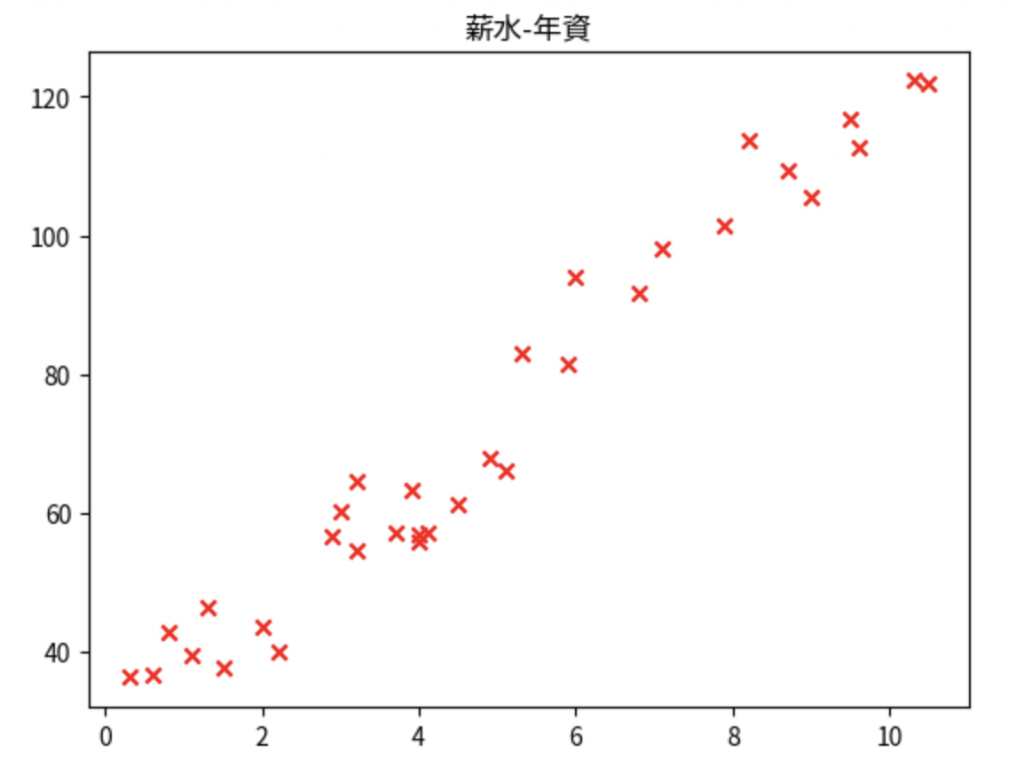
w = 0
b = 0
y_pred = w*x + b
plt.plot(x, y_pred)
plt.show() 

補上原始資料點：

w = 0
b = 0
y_pred = w*x + b
plt.plot(x, y_pred, color = "blue", label = "預測線")
plt.scatter(x, y, marker = "x", color = "red", label = "真實數據")
plt.title("薪水-年資")
plt.xlabel("年資")
plt.ylabel("月薪(千)")
plt.legend()
plt.show() 

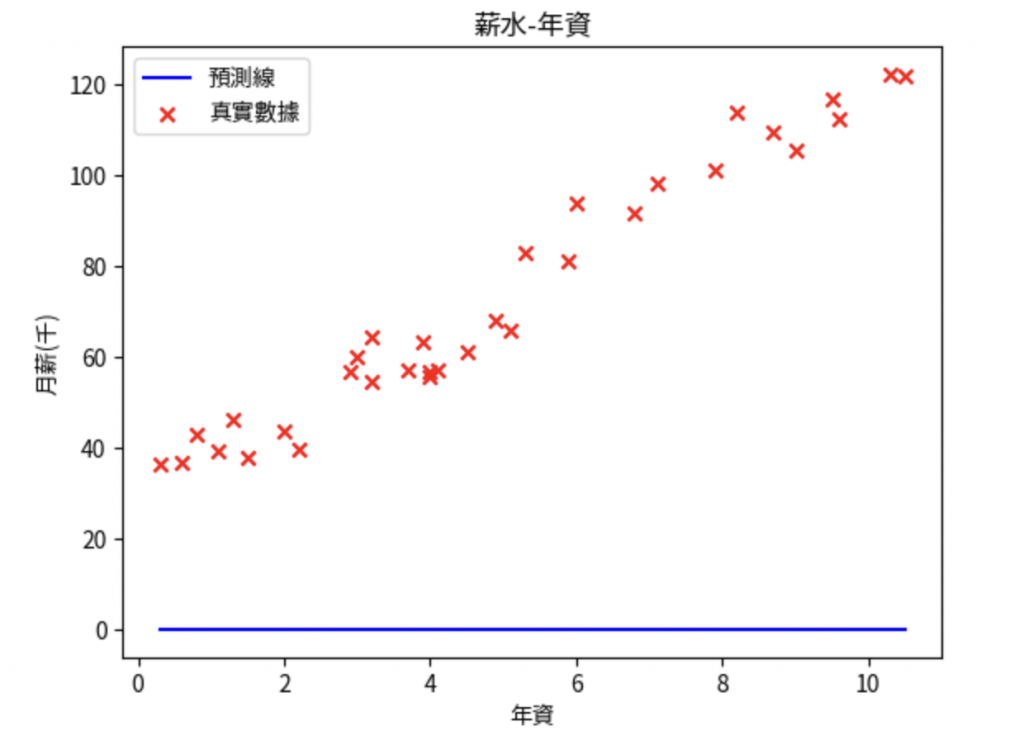
目標：找出最符合資料點的直線

5. 將上述的公式寫成一個函式來方便帶入w跟b

def plot_pred(w, b):
    y_pred = w*x + b
    plt.plot(x, y_pred, color = "blue", label = "預測線")
    plt.scatter(x, y, marker = "x", color = "red", label = "真實數據")
    plt.title("薪水-年資")
    plt.xlabel("年資")
    plt.ylabel("月薪(千)")
    plt.legend()
    plt.show() 

plot_pred(0, 0) #輸入(0, 0)，輸出圖片與上述相同

6. 最適合資料的直線?
   如何挑選？=> 可以去尋找資料點與直線的距離，去推估最吻合的直線。
   如何推估？=> 資料點減掉直線上的值，算出平方誤差，可以寫成一個函數。
   函數？=> 成本函數(cost function)，cost = (真實數據-預測值)^2

#cost function
w = 10
b = 0
y_pred = w*x + b 
cost = (y - y_pred)**2 
cost
cost.sum() ＃輸出：19884.080000000005
cost.sum() / len(x) ＃距離平方的平均：602.547878787879

cost的輸出

將上述運算寫成函式：

def compute_cost(x, y, w, b):
    y_pred = w*x + b
    cost = (y - y_pred)**2
    cost =  cost.sum() / len(x) 

    return cost 

compute_cost(x, y, 10, 10) ＃輸出：227.88121212121214

如果w的值從-100~100時，會有什麼樣的結果：

costs = []
for w in range(-100, 101):
    cost = compute_cost(x, y, w, 0)
    costs.append(cost)
costs

plt.scatter(range(-100,101), costs)
plt.show()

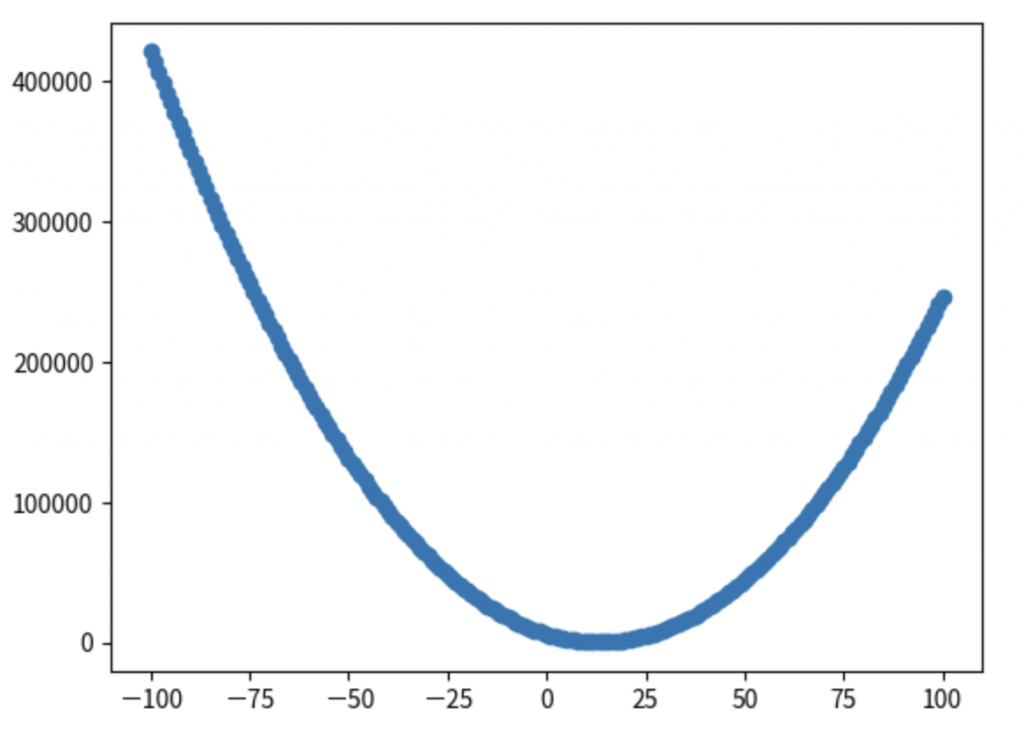
如果w 和 b 都範圍從-100~100的話？

ws = np.arange(-100, 101)
bs = np.arange(-100, 101)
costs = np.zeros((201, 201))

i = 0
for w in ws:
    j = 0
    for b in bs:
        cost = compute_cost(x, y, w, b)
        costs[i, j] = cost
        j = j + 1
    i = i + 1

costs

畫出w, b所對應到的cost

ax = plt.axes(projection = "3d")
ax.xaxis.set_pane_color((0, 0, 0))
ax.yaxis.set_pane_color((0, 0, 0))
ax.zaxis.set_pane_color((0, 0, 0))
ax.view_init(45, -120)
plt.figure(figsize =  (7,7))

b_grid, w_grid = np.meshgrid(bs, ws)

ax.plot_surface(w_grid, b_grid, costs, cmap = "Spectral_r", alpha = 0.7)
ax.plot_wireframe(w_grid, b_grid, costs, color = "black", alpha = 0.1)
ax.scatter(ws[w_index], bs[b_index], costs[w_index, b_index], color = "red", s = 40)
ax.set_title("w_b_對應的cost")
ax.set_xlabel("w")
ax.set_ylabel("b")
plt.show()

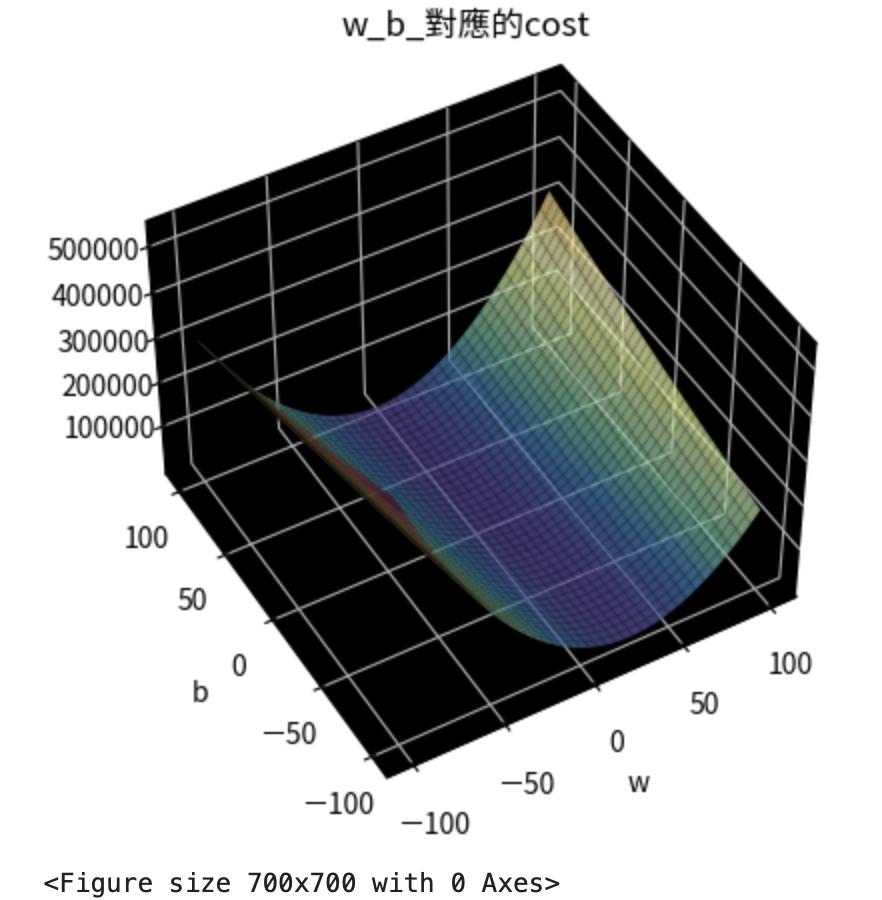
找出cost最低點所對應到的(w, b)

w_index, b_index = np.where(costs == np.min(costs))
print(f"當w = {ws[w_index]}, b = {bs[b_index]}，會有最小cost: {costs[w_index, b_index]}") 
#輸出：當w = [9], b = [29]，會有最小cost: [32.69484848]

7. 如何有效率找出最佳的w和b
   可以利用gradient descent(梯度下降)，也就是根據斜率去改變參數
   原本的cost = (真實數據-預測值)^2，也就是cost = (y-y_pred)^2，若將y_pred = w．x + b，且b假設為0帶入，可以得到(y-wx)^2，若將其微分，則可以知道切線斜率，就能利用gradient descent(梯度下降)來找出最佳的組合(切線斜率相當接近0)。
   

詳細參考：GrandmaCan -我阿嬤都會教學影片

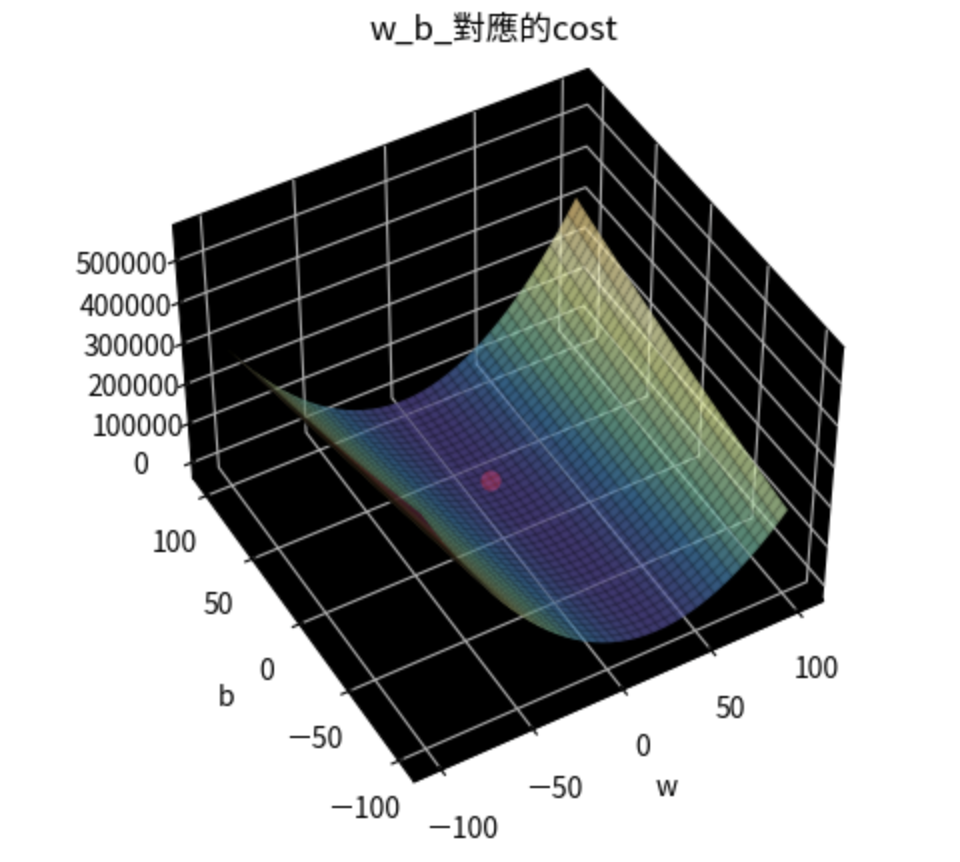
=>下一篇繼續更新如何有效率找出最佳的w和b的部分