量子電腦的崛起與傳統密碼學的隱憂

隨著量子計算技術的快速發展，主流的公鑰加密技術如 RSA 和 ECC （橢圓曲線密碼學）可能無法再確保資訊的安全性。原因在於 RSA 所依賴的「大數因數分解問題」和 ECC 所基於的「橢圓曲線離散對數問題」都可能被量子演算法（例如 Shor 演算法）快速破解。

密碼學家於是將焦點放在能抵禦量子電腦的數學問題，設計「後量子密碼學」，也稱為「抗量子密碼學」。旨在設計「即使量子電腦出現，也能保持安全性」的加密系統。其核心是基於新的數學難題，例如：

• 晶格問題
• 多變量多項式問題
• 雜湊函數碰撞難題
• 編碼理論難題

然而，這些問題並不如直因數分解或離散對數問題那樣直觀後好理解。趁著這次的三十天鐵人賽，我希望在這裡分享個人在學習後量子密碼學上的心得。

預計涵蓋內容

相關數學知識：

在介紹每個密碼學主題時，順帶介紹所需的數學知識，包括（聽到爛的）模算數、多項式模算數、晶格（Lattices）、多變量二次方程組、雜湊函數、和編碼理論等。這些數學概念對於理解和實作後量子密碼學協議至關重要。

SageMath 密碼學實作

SageMath(https://www.sagemath.org) 是我研究後量子密碼學的主要工具。SageMath 是一款基於 Python 上的開源數學計算軟體，方便操作且已經定義好許多複雜的數學結構運算。為了不要把整個篇幅搞得都是數學，儘量多一些可以實作的部分:

我們會透過 SageMath 實際執行：

• 建構密鑰（Key Generation）
• 加密（Encryption）和解密（Decryption）
• 簽章（Signature）和驗章（Verification）
• 嘗試破解（Attack）以測試安全性

晶格密碼學（Lattice Based Cryptography）

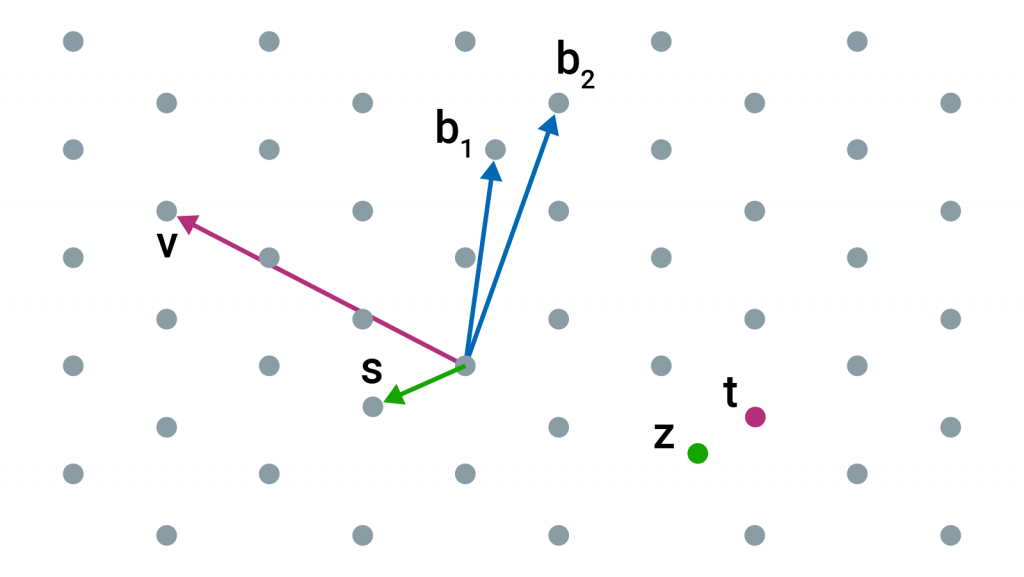
晶格密碼系統的是基於在高維度空間中尋找「短向量」或求解「最近向量問題」的困難問題，故被視為量子安全。本系列文章會講解 NTRU 密碼系統

優勢：速度相對快，可支援同態加密（Homomorphic Encryption）等進階功能。
挑戰：密文長度與金鑰大小較傳統 RSA 或 ECC 大。

多變量二次方程密碼學（Multivariate Quadratic Based Cryptography）

此類密碼系統採用「多變量二次方程組」作為核心難題，代表演算法如 Rainbow 等。

• 優勢：簽章速度快。
• 挑戰：公鑰體積通常非常大，需要更多儲存空間。
  

雜湊函數密碼學（Hash Based Cryptography）

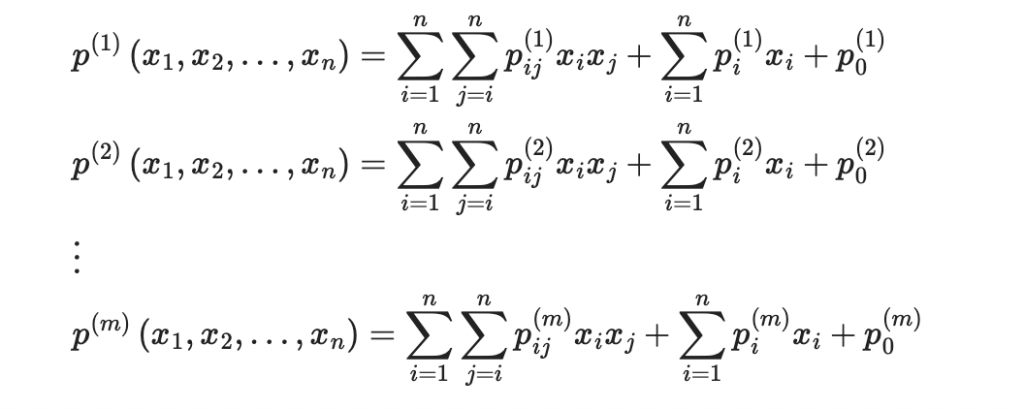
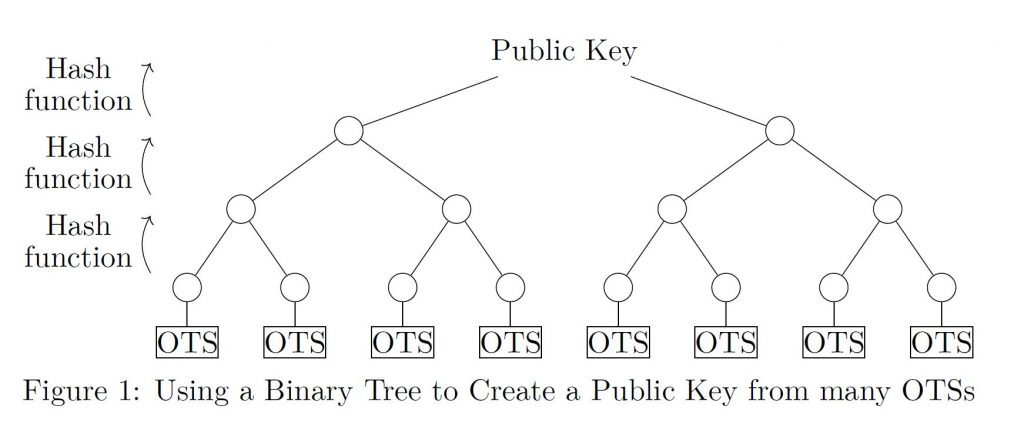
雜湊函數密碼學常見於 Winternitz one-time signature、Merkle Tree 等。因雜湊函數（如 SHA-2、SHA-3）在量子攻擊下仍保有高強度安全性，因此用於構建「不可竄改」的簽章機制。

• 優勢：安全基礎建立在知名且經過廣泛審計的雜湊演算法。
• 挑戰：部分方案需要複雜的鍵管理。
  

編碼密碼學（Code Based Cryptography）

著名的實例為 McEliece 加密系統，基於 糾錯碼（Error-Correcting Codes），如 Goppa codes。

優勢：在量子攻擊下仍具高安全性，數十年歷史無重大漏洞。
挑戰：公鑰極大化，同樣需要較多儲存空間。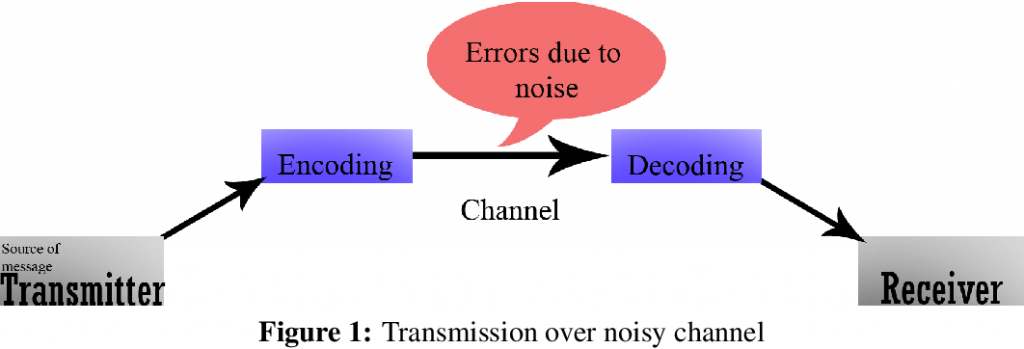

後量子密碼學未來發展與應用

隨著量子計算技術不斷演進，後量子密碼學勢必將成為下一代的核心安全機制。無論是 政府軍方、金融機構，還是 物聯網（IoT） 與 區塊鏈技術都需要及早佈局，確保資訊安全能夠抵禦量子電腦的衝擊。

• 國際標準發展：NIST（National Institute of Standards and Technology）已經著手制定後量子密碼學標準。
• 商業應用落地：企業開始評估將 Lattice-Based 或 Code-Based 系統整合進現有基礎架構。
• 學術研究熱潮：在可用性與效率上，還有許多優化空間，有賴研究人員不斷深入探討。

ref:

https://utimaco.com/service/knowledge-base/post-quantum-cryptography/what-lattice-based-cryptography

https://www.isara.com/blog-posts/hash-based-cryptography.html

Singh, Harshdeep. "Code based cryptography: Classic mceliece." arXiv preprint arXiv:1907.12754 (2019).