圖形(Graph)是由所有頂點的集合 (V) 和所有邊的集合 (E) 所組合而成,通常以 G=(V, E) 來表示。
圖形結構分成以下兩種種類:
無向圖形
無向圖形的邊可以雙向通行,通常使用沒有箭頭的邊,並以 (V1, V2) 表示頂點V1和頂點V2相臨的關係。如下圖所示: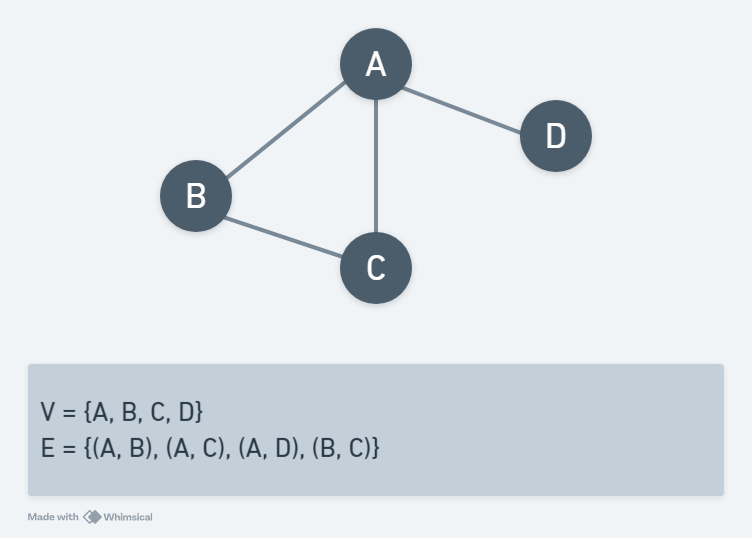
有向圖形:
有向圖形的邊可以理解為單行道,通常使用沒有箭頭的邊,並以 <V1, V2> 表示頂點V1到頂點V2頂點的關係。如下圖所示: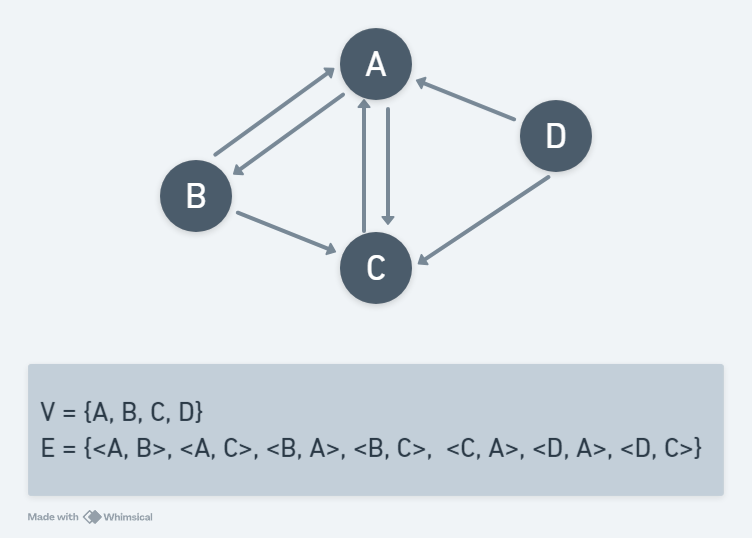
圖形資料表示法
相鄰矩陣法(Adjacency Matrix)
如圖所示: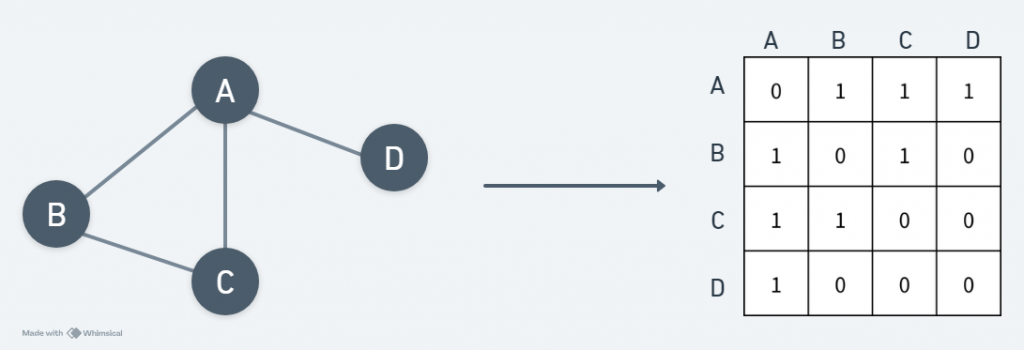
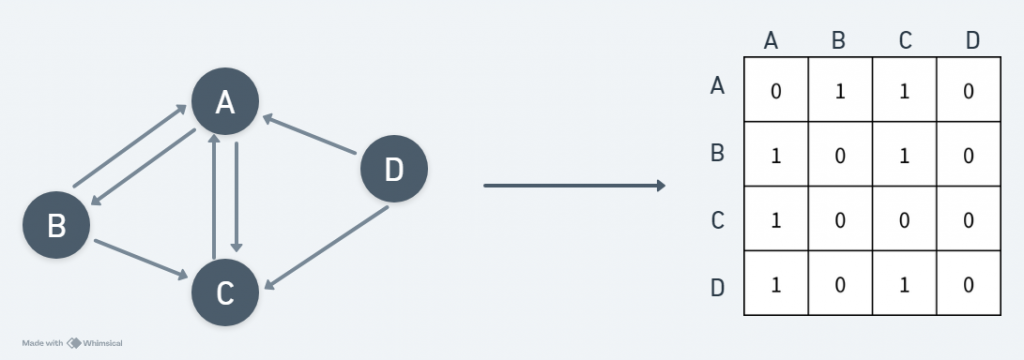
優點:
缺點:如果圖形的邊不多的話,會造成稀疏矩陣,導致空間浪費。
相鄰串列法(Adjacency List)
如圖所示: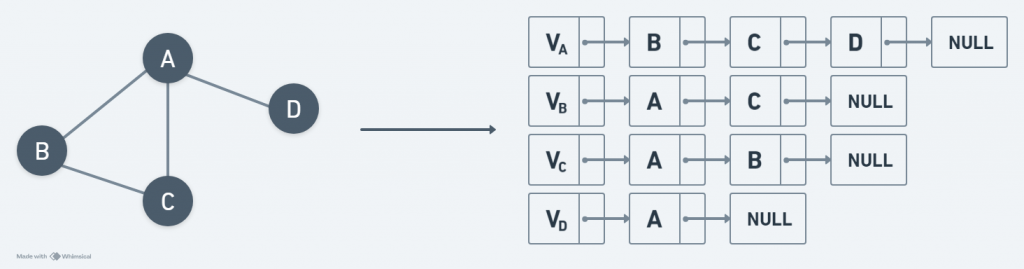
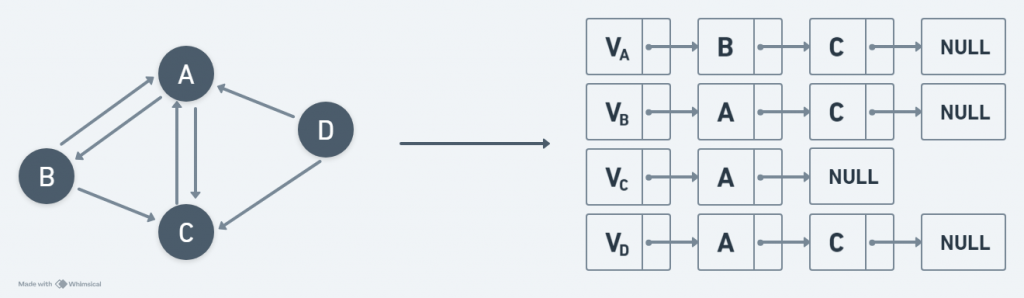
優點:比相鄰矩陣法節省空間。
缺點:因為串列鏈結圖形加入或刪除邊的操作較為麻煩且費時。
相鄰複合串列法(Adjacency Multilist)
如圖所示: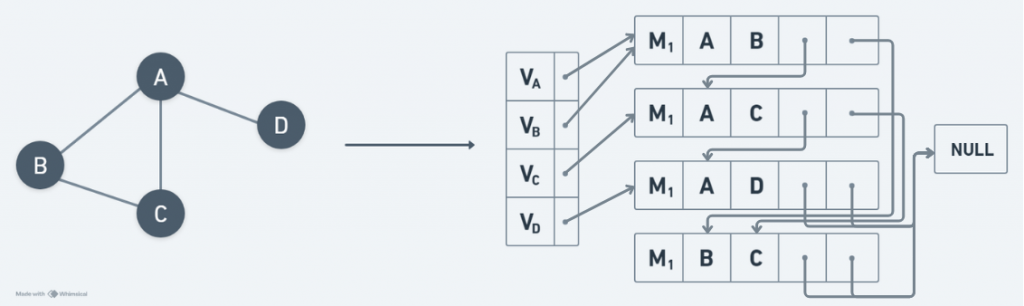
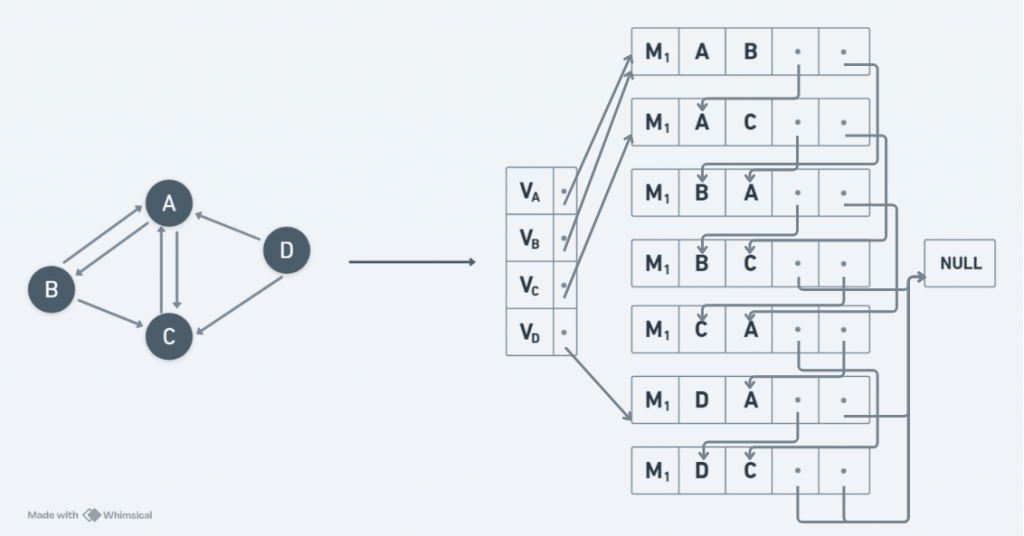
優點:
缺點:查詢特定邊是否存在可能需要遍歷多個指標鏈接。
索引表格法(Index Table)
如圖所示: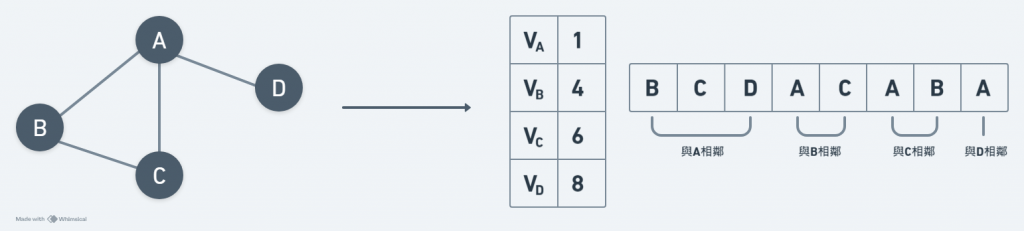
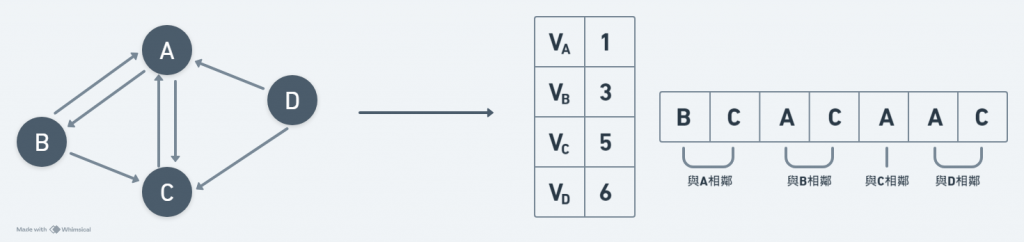
優點:比相鄰矩陣法節省空間。
缺點:不能直觀看出各鄰接頂點的信息,需要進一步查找。
參考資料:
