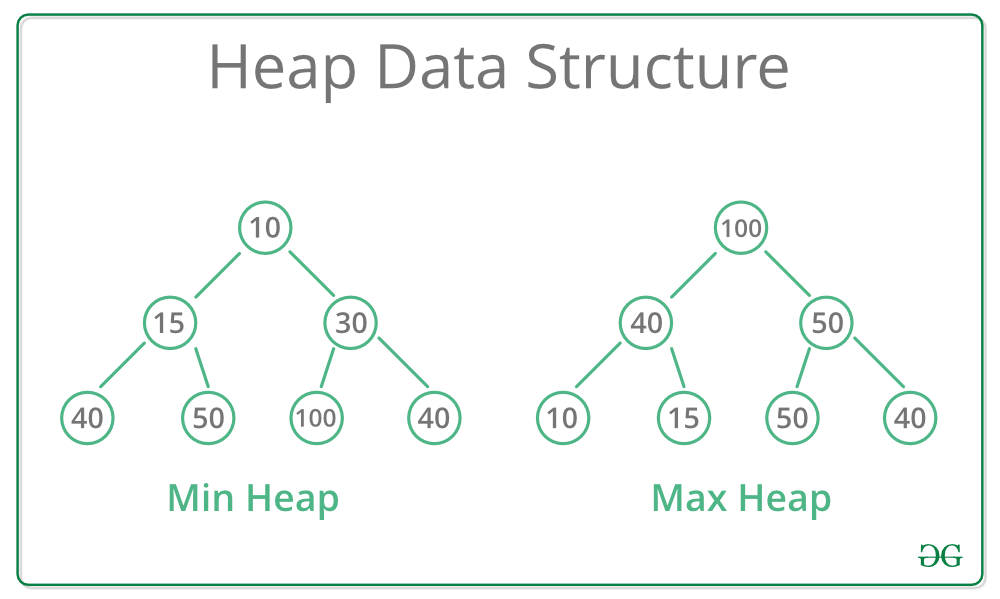
今天要來介紹新的結構，堆積（Heap）

何謂 Heap：以 Max-Heap 為例

Heap 是一棵 Binary Tree，可為空樹，若非空，則：

1. 一定是 Complete Binary Tree
2. 每個父節點值必大於子節點值
3. root 是 max value
   圖示：來源
   

heap 的應用

Priority Queue

在系統中常常有這樣的佇列，他並不是 FIFO 的結構，而是會輸出 Priority 最高的元素。例如說：OS 採用 Priority Scheduling Algorithm 的 Ready Queue。
這時候使用 Heap 就特別適合來實作，因為，最大的元素就在 root！
只需要 O(1) 時間就好。

Heap Sort

使用 Heap 也可以進行排序，接下來有機會講到排序再說說。

Heap 的保存方法

因為 Heap 是 Complete Binary Tree，在前面有說過，使用 array 來儲存可以充分利用空間。

heap 的 operation

heap 節點的插入（Insert x）

1. 一定要將 Node X 置入最後節點的下個位置，因為要滿足 Complete Binary Tree。
2. 置入後，開始向上調整，如果 x 比現在的 parent 大，則兩者互換，繼續挑戰 grandparent。
3. 直到滿足 Heap 定義，即可停止。

圖示：

heap 刪除最大值（delete MAX）

1. 將最後一顆節點取代 root，才能滿足 Complete Binary Tree 條件。
2. 從 root 開始向下調整，向下調整又叫做 Heapify。

heapify 向下調整

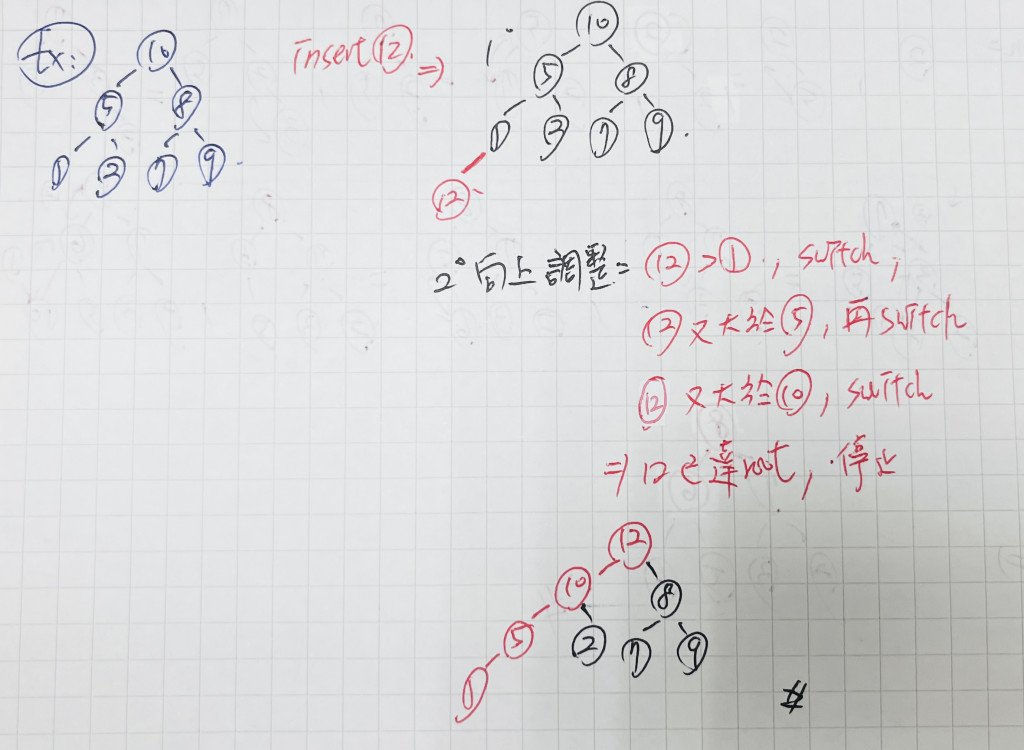
假設某樹的 root 為 X，則此樹的 Heapify 的動作為

1. 令 root 的兩個 child 為 y1, y2
2. 求出 y1, y2 兩者的最大值 Y
3. 如果目前的 root 大於 Y，則調整完成。（root 所在位置正確）
4. 如果目前的 root 小於 Y，則代表 root 所在位置不正確。因此與 Y 調換位置，並且重新 Heapify 目前 root 為 X 之樹，直到完成調整。

建立 Heap

top-down method：利用連續的 insert 來建立 heap

例如：給予 2 5 7 3 8 6 9 利用 top-down method 來建立

Ans: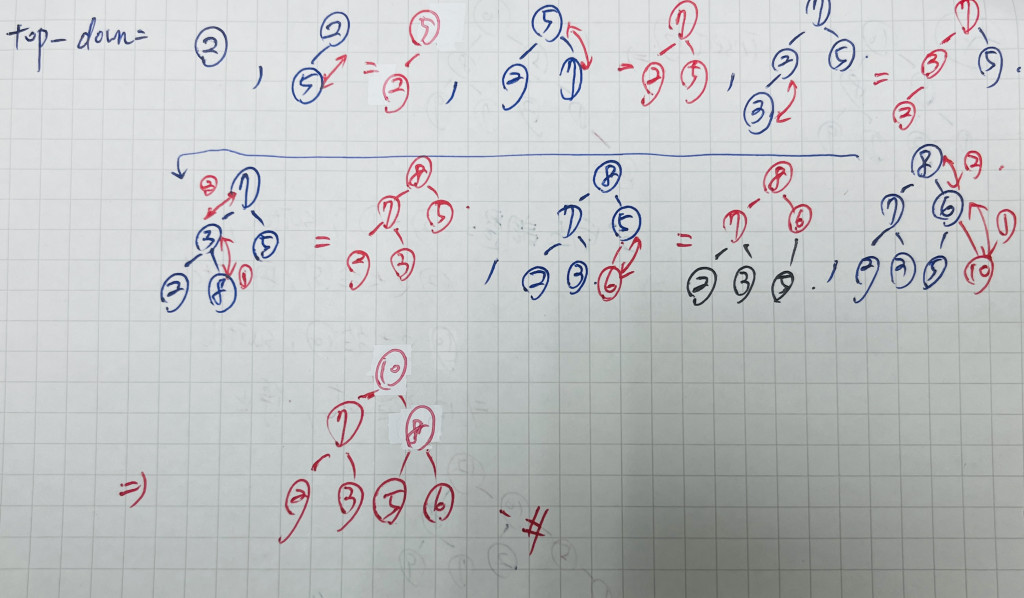

時間分析：如果插入 heap 時 i 個 nodes，那麼就要做 log(i) 次的比較，這個 log 是 2 為底，假設目前有 n 個 data 要 insert，那麼總共要 sigma 1~n(log i) 比較 = log1+log2+log3+.......logn = log(n!) = O(nlogn)

因此，top-down method 的 time complexity 為 O(nlogn)

bottom-up method：從最後一個父節點開始做 heapify

例如：給予 2 5 7 3 8 6 9 利用 bottom-up method 來建立

Ans:

時間分析：

1. 假設 heap 的高度為 H，如果某 parent 位於高度 i，則最多需要調整 H - i 次
2. 高度 i 的節點數，根據 binary tree 定理，最多有**2^(i - 1)**個
3. 因此 level i 的所有節點最多需要調整：2^(i - 1) * (H - i) 次
4. 整棵樹由高度1 ~ H：最多需要調整 sigma 1 ~ H(2^(i - 1) * (H - i)) 次

解出這個式子後，得到2^H - 2 - (H - 1) = 2^H - H - 1 次

又因為 heap 為 complete binary tree，數高為 log(n + 1) 向上取整數（ceiling），或是 logn 向下取整（floor）後 + 1（其中 n 為節點總數）。此數趨近 log n，所以將 logn 帶入前式之 H，得到 n - logn - 1 = O(n)

因此，buttom-up method 的 time complexity 為 O(n) 線性時間，因此比 top-down method 更有效率。

小結

heap 是個非常重要的結構，今天先介紹 heap 的操作，明天再來介紹他的程式碼