DAY 8 試題

問題描述

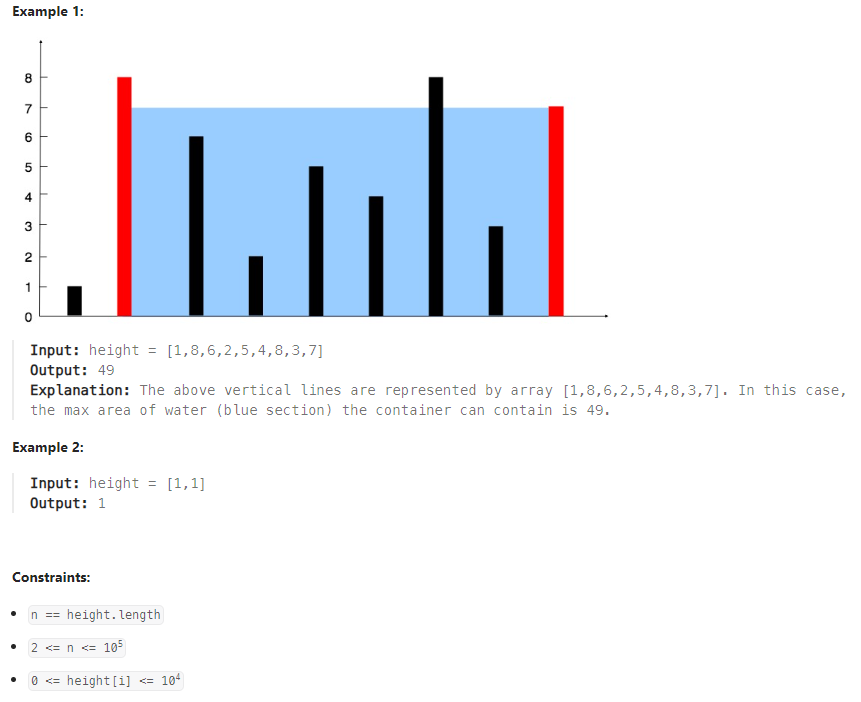
給定一個整數陣列 height，每個值代表對應位置上的垂直線高度，這些垂直線與 x 軸形成容器。請找到兩條垂直線，與 x 軸組成一個容器，該容器可以儲存的最多水量。容器的水量由兩條垂直線之間的最短線高度決定，乘以它們之間的距離。

範例 1：

• 輸入: height = [1,8,6,2,5,4,8,3,7]
• 輸出: 49
• 解釋: 兩條垂直線分別位於 index 1 和 index 8，其高度分別為 8 和 7。它們之間的距離為 7，因此能形成的容器最大面積為 7×7=49。

範例 2：

• 輸入: height = [1,1]
• 輸出: 1
• 解釋: 兩條垂直線高度相同且距離為 1，因此儲水量為 1×1=1。

解題思路

這道題的關鍵是如何找到兩條垂直線，使得它們組成的容器面積最大。容器的面積可以表示為兩條垂直線的高度中的較小值，乘以它們之間的距離。

我們可以使用雙指針法來高效地解決這個問題。具體步驟如下：

1. 初始化兩個指針，分別指向陣列的左右兩端。
2. 計算由這兩條線組成的容器面積。
3. 根據這兩條線的高度，將指針向內移動：移動較短線的指針，因為要獲得更大的面積，需要增加短邊的高度。
4. 重複這個過程，直到兩個指針相遇為止。
5. 返回最大的容器面積。

這樣的雙指針法能夠將問題從暴力枚舉的𝑂(𝑛^2)降低到𝑂(𝑛)的時間複雜度。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1; // 左右指針
        int max_area = 0; // 儲存最大面積

        // 雙指針法
        while (left < right) {
            // 計算目前兩條線形成的面積
            int h = min(height[left], height[right]);
            int area = h * (right - left);
            max_area = max(max_area, area);

            // 移動較短的指針
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }

        return max_area;
    }
};

解法重點與分析

雙指針初始化：

• 左指針 left 初始化為 0（最左邊的線），右指針 right 初始化為陣列的最後一個元素（最右邊的線）。

迴圈處理：

• 當左指針小於右指針時，計算兩者之間的容器面積，並更新最大面積 max_area。
• 如果左邊的線比較短，則將左指針向右移動；反之，移動右指針。這樣可以確保每次嘗試時，可能獲得更大的面積。

時間複雜度：

• 由於每次迴圈會移動一個指針，這個算法的時間複雜度為𝑂(𝑛)，其中 n 是陣列的長度。

總結

這題的重點在於如何通過雙指針法來有效地計算出最大儲水容器的面積。這種方法的優勢在於它能夠在不需要暴力枚舉的情況下，以線性時間解決問題。雙指針的策略是基於面積的公式和容器的性質，即面積由兩條邊的較小值決定，因此每次移動較短的一邊來獲得更好的結果。

以上是第八天的自學內容分享，謝謝大家。