對稱/非對稱加密 （附數學推導生成密鑰與加解密過程）

對稱式加密

對稱式加密是 使用同一把密鑰對資料進行加解密，常用的對稱加密算法包括：

• DES (Data Encryption Algorithm)

• 3DES (Triple DES)

• AES (Advanced Encryption Standard)

對稱加密算法優點是算法公開，計算量小，加密速度快，加密效率高。缺點是一但密鑰失竊，加密資料就會被公開，也無法確認消息是誰發出的，因為真正的密鑰真正的主人跟竊賊都使用同樣密鑰。

區塊鏈中不會使用對稱加密算法。

非對稱式加密

非對稱式加密就是加解密雙方使用不同的密鑰進行資料交互。這一對密鑰被稱作 公鑰（public key）私鑰 (private key)。非對稱式加密可以加密要傳遞的資料，也可以驗證數位簽章，保證不可否認性。

私鑰只有擁有者才知道，公鑰由私鑰當參數計算生成，且是公開的。

公鑰加密只能私鑰解密，私鑰加密也只能由公鑰解密，加解密需要非對稱的兩把鎖才能完成，所以叫做 "非對稱加密"。

先講一下公私鑰的使用情境之後，再介紹一下公私鑰生成過程。

使用情境

Scenario: 消息發送方 B 發送一個消息 給 A。

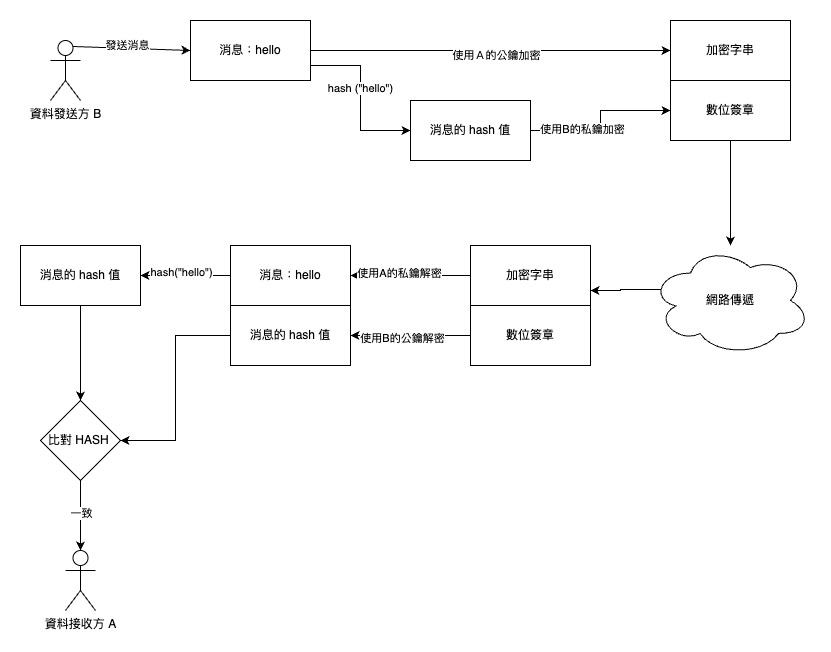
1. B 將消息使用 A 的公鑰加密，變成加密字串。同時對消息原始明文進行一次 HASH 壓碼。然後使用自己的私鑰對 HASH 值進行加密形成數位簽章。

2. 透過網路傳遞 加密字串，數位簽章 給 A。

3. A 收到資料後，先把加密字串用自己的私鑰解密得到消息明文。然後針對數位簽章使用 B 的公鑰解密得到 HASH 值。

   為了驗證消息的發送方真的是 B，對明文消息進行一次 HASH，比對這個 HASH 是不是跟數位簽章解密後的內容一致。

以上就是非對稱式加密的使用情境。

擴充知識：公私鑰的產生與加解密過程

Asymmetric cryptography 非對稱密碼學

這邊我們將研究並解析非對稱加密中比較知名的實現之一：RSA 公私鑰的生成與加解密技術內幕。

RSA Key 的生成

1. 選擇兩個主要的數字 p 與 q，所選的 p 和 q 必須為質數。

   p = 61
   q = 53
   

2. 計算 p q 乘積 n:

   n = p * q // n = 3233
   

   n = 3233

3. 計算由拉數 Euler's totient function ϕ(n)。

   ϕ(n) = (p-1)*(q-1)
   

   ϕ(n) = (61-1)*(53-1) = 3120

4. 選擇一個公鑰指數 e，且 e 需要滿足以下條件：

   1. e 必須與 ϕ(n) 互為質數，且必須小於 ϕ(n)。

      ps: 如果兩個或兩個以上的整數的最大公因數是1，則稱它們為互質

      這邊選 e = 17

5. 選擇一個私鑰指數 d:

   使用 Extended Euclidean Algorithm 計算出 d:

   目前我們的 e = 17, ϕ(n) = 3120

   e*d 除以 ϕ(n) 餘數要等於 1:

   (17 * d) mod 3120 = 1
   

   得出 d = 2753

   目前目前我們得出了一對公私鑰：

   • Public Key (e, n) -> Public Key (17, 3233)
   • Private Key (d, n) -> Private Key (2753, 3233)

使用公鑰加密：

加密一個 message 下面以 m 代替。

1. 把 m 變成數字且 0 <= m < n

2. 用公式計算密文 c：

   

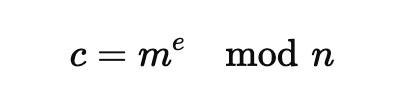
   假設 m 是 65，我們要把 65 進行加密：

   c = (65^17) % 3233
   

   得到密文 c = 2790

使用密鑰解密：

1. 使用公式計算明文 m：

   

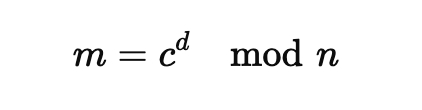
   已知密文是 c = 2790

   m = (2790^2753) % 3233
   

   得到明文 m = 65

RSA 實現總結

1. 公私鑰的生成需要選擇兩個數字 p 與 q，然後計算 n 與 ϕ(n)，並進一步算出公鑰用的 e 與 私鑰用的 d。

2. 使用公鑰 key(e, n) 加密明文 m 得到密文 c: c = (m^e) % n

3. 使用私鑰 key(d, n) 解密密文 c 得到明文 m: m = (c^d) % n

當我們持有某人的公鑰時，我們是有機會可以透過計反推出他的私鑰的，不過要知道他建立公私鑰時的 p 與 q 是多少。

當然，實際上的 RSA p 與 q 的選擇一定不會只是簡單的 61 與 53 這樣而已。選擇的數字越大就越難破解。這就是目前 RSA 加密算法安全的保障。