PLONK可以用於建立通用的ZK-SNARK。
對於一般的ZK-SNARK電路，是由 Interactive Oracle Proof (IOP) 與 Polynomial Commitment Scheme (PCS) 組合而成的。
IOP 的作用是提供一個建立證明所需的證明者和驗證者之間的交互作用。由於IOP只是一個理論對象，要將它實現出來，就需要利用PCS來實例化。PCS 就可以讓證明者提交一個多項式，讓驗證者可以選擇任何點打開該多項式及進行驗證，此外，證明者需要說服驗證者相信他所發出的多項式證明是能夠滿足所有需要驗證的條件。當要記住，現在仍然是一個交互式零知識證明。然後可以使用 Fiat-Shamir heuristic 令到交互式零知識證明可以轉換為非交互式零知識證明。
另外， SNARK 有簡潔的特性，所以需要確保證明是簡短的及能夠進行快速驗證。換言之，就是證明大小和驗證者進行驗證的時間最多應該是多項式次數的degree。

PLONK 的組成部分是算術化和 polynomial IOP。
PLONK IOP 是一個多項式，其中證明者需要說服驗證者相信他的證明，對於公共電路 C 和語句 x，會有一個證人 w，令到 C(x,w) = 0。這表示PLONK IOP可以與PCS配合使用來創建通用SNARK。

PLONK 預處理是不需要進行可信任設置，所以表示:
如果將 PLONK IOP 與不需要可信任設定的 PCS 進行匹配，那麼最終的 SNARK 就沒有可信設定。
如果將 PLONK 與確實需要可信設定的 PCS 結合起來，那麼最終的 SNARK 將需要可信設定。
根據結合 PLONK 的 PCS，最終會做出不同的權衡，這取決於所選 PCS 的屬性和加密假設。

算術化

Plonkish算術化是PLONK證明系統特有的算術化。在Plonkish出現之前，其實主流的電路表達形式都是為RICS，而這表達形式已被多個零知識證明算法所使用，包括Groth16。

學習加法門和乘法門在運算符中的區分

• 以下是一個電路例子:

1. 有3個門、6個輸入及1個輸出。
2. 滿足了3個約束。
   • X1 + X2 = X6
   • X3 * X4 = X5
   • X6 * X5 = OUT

• 以下是一個矩陣W表格:

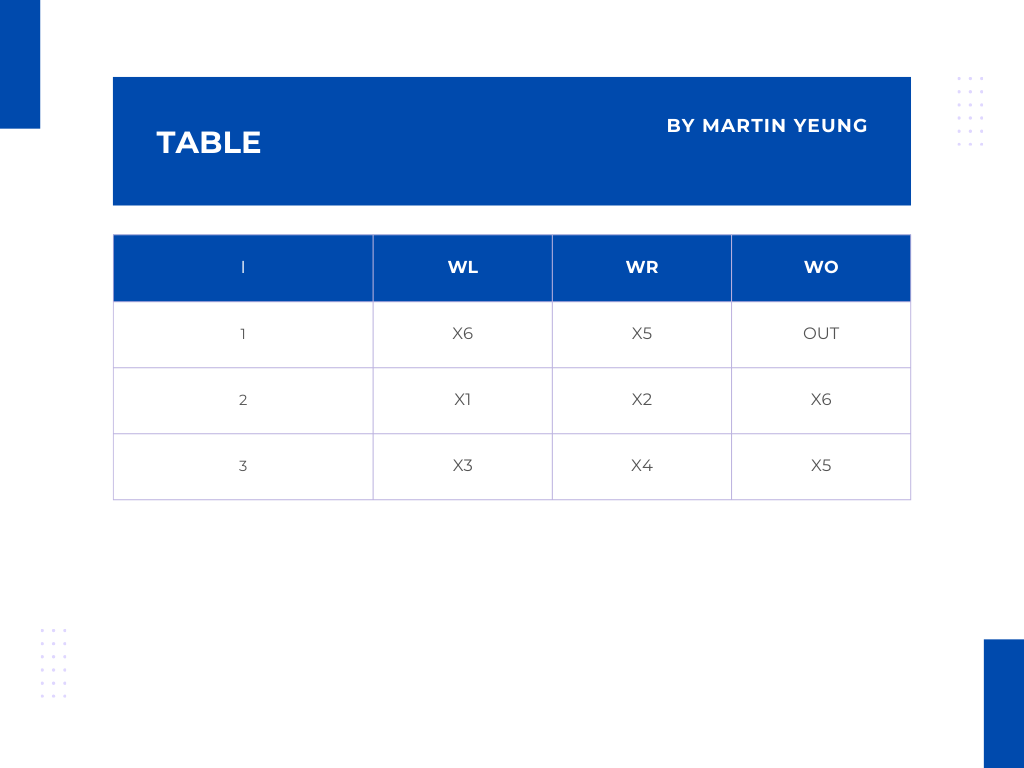
• 在表格中的第1行是各欄的標題，i是指門、 WL是指左輸入、WR是指右輸入及WO是指輸出。
  第1列是指第1個門，會看到X6是指左輸入、X5是指右輸入及OUT是指輸出。
  第2列是指第2個門，會看到X1是指左輸入、X2是指右輸入及X6是指輸出。
  第3列是指第3個門，會看到X3是指左輸入、X4是指右輸入及X5是指輸出。

• 為了能對加法門和乘法門進行區分，會以這個矩陣Q表格作展示:

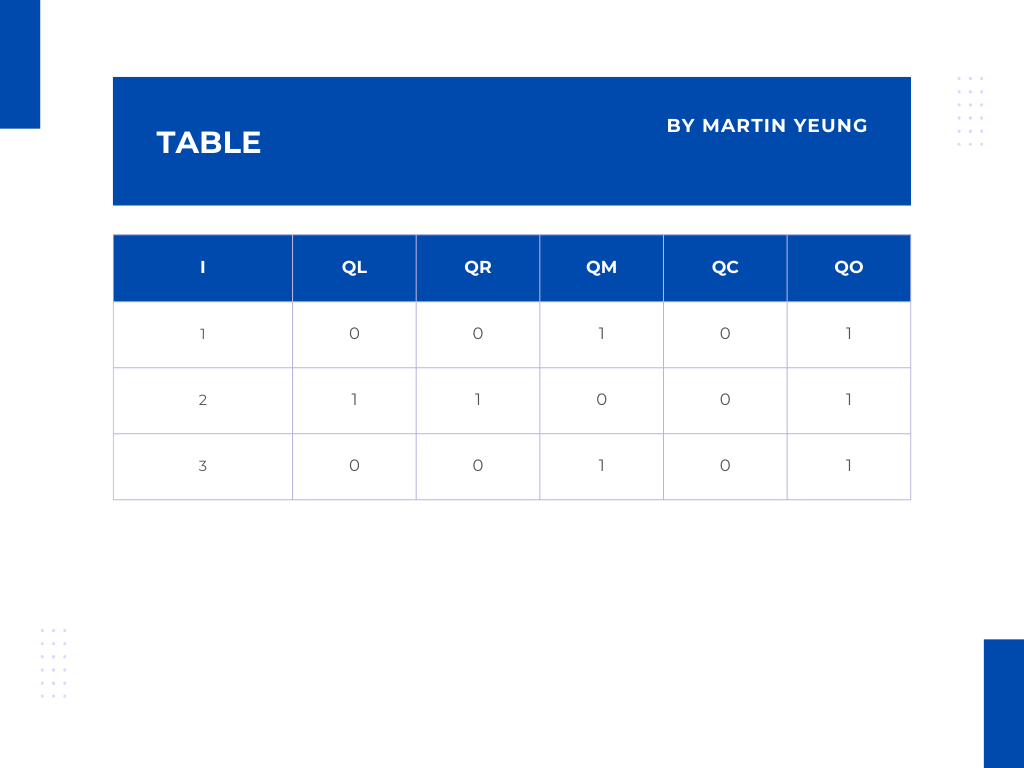
• QL 和 QR 來表示加法門的輸入

• QL 是指左輸入

• QR 是指右輸入

• QM 表示乘法門

• QC 表示常量的數值

• QO 表示輸出