今天就講解算術化的重點，算術電路是透過帶有加法門和乘法門的電路來描述當中的程序。需要將一般程式轉換為代數的原因是當使用橢圓曲線或者是其他加密基元時，其實無法有效地驗證電腦程式字節碼的操作，從而使到可以有效地去評估很複雜的代數表達式。

從算術步驟獲得到的電路描述可以轉換為多項式恆等式。這表示使用算術化來獲得一組證明多項式性質的方程式。這能夠透過多項式表示算術門的多個實例，從而簡潔地表示出來。不過當程序越複雜，需要處理的多項式的次數就越高。利用使用多項式的關係，可以將大量的電路資訊壓縮成為多項式的表示形式，無論階數如何，多項式的大小都具有固定的大小。例如，可以將具有數百萬個、千萬個的變數向量加入到多項式中，然後對該多項式執行算術運算，就好像它是法向量一樣。

約束

1. 電路約束
   就是一些條件約束，每一個約束都表示一個條件限制。
2. 複製約束
   就是從輸出和輸入形成一種關連，可以再次看一看下面的圖表，由於在矩陣W表格中，可以看到第1個門的左轉入W6不一定等於第2個門的輸出X6。所以需要加入複製約束來確保第1個門的左轉入W6一定等於第2個門的輸出X6。也可以看到加入複製約束可以讓輸出的值會等於另一輸入的值，形成一種關連，而不是各自各的約束。
   

Lagrange Polynomials and interpolations (拉格朗日多項式和插值)

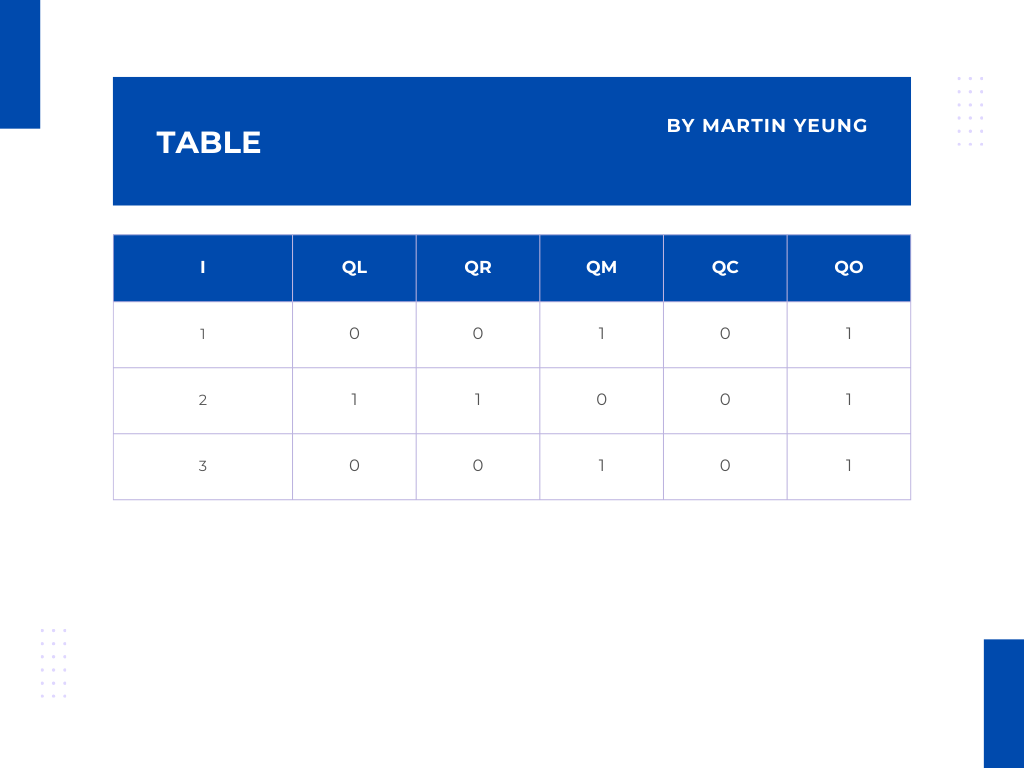
在PLONK中需要證明者向驗證者提交多項式證明，所以需要插入一個對整個執行追蹤進行編碼的多項式。這表示需要將所有輸入和所有電線編碼為一些多項式。 證明者可以用Fast Fourier transform (FFT)計算多項式的係數，多項式的次數與門的數量成正比。例如，如果編碼給我們100 個約束，則相應的多項式的次數最多為99。
由於透過向量描述的任何算術電路都可以轉換為拉格朗日多項式(Lagrange Polynomials)表示，因此將向量表示為拉格朗日多項式的線性和會更為合適。因為當使用拉格朗日插值時，全域參數是多項式的拉格朗日的係數，所以提供了多項式的有效點值的表示。
拉格朗日多項式讓我們可以利過多項式來表示向量，更可以確保所有用於向量的任何關係也同樣能夠用於多項式。因此當使用向量來評估門的方法，就可以利用拉格朗日多項式將這些向量轉換為多項式。

例子解說

矩陣W表格可以說是證明者需要準備的資料，當準備好之後，可以進行編譯。完成後編譯，可以將結果發送給驗證者。
現在在矩陣W加多一項約束，約束是最終輸出是99。因此，新增一條約束後的矩陣W表格會是這個: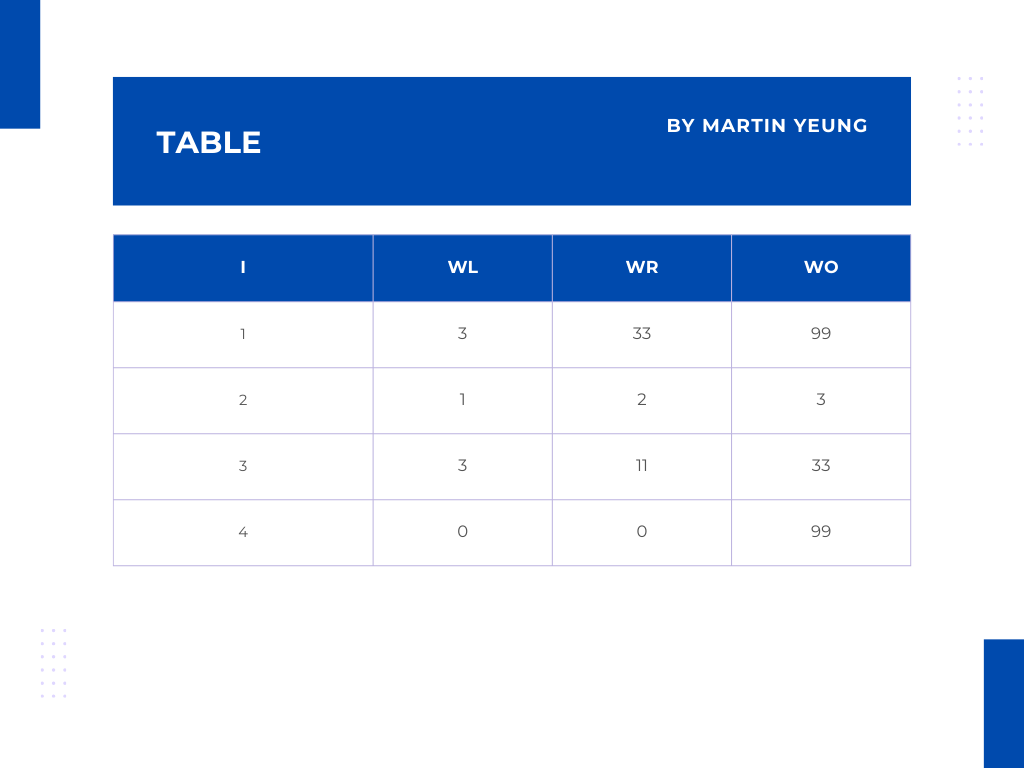

• 由於只是新增輸出一項約束，不會影響算術門的數量及輸入的值。

假設參數:

• 第1列是指第1個門，左輸入X6是3、右輸入X5是33及OUT輸出是99。
• 第2列是指第2個門，左輸入X1是1、右輸入X2是2及X6是3。
• 第3列是指第3個門，左輸入X3是3、右輸入X4是11及X5是33。
• 第4列是沒有指向任何門，只是其中一個輸出約束，左輸入是0、右輸入是0及輸出是99。

另外，新增一條約束後的矩陣Q表格會是這個: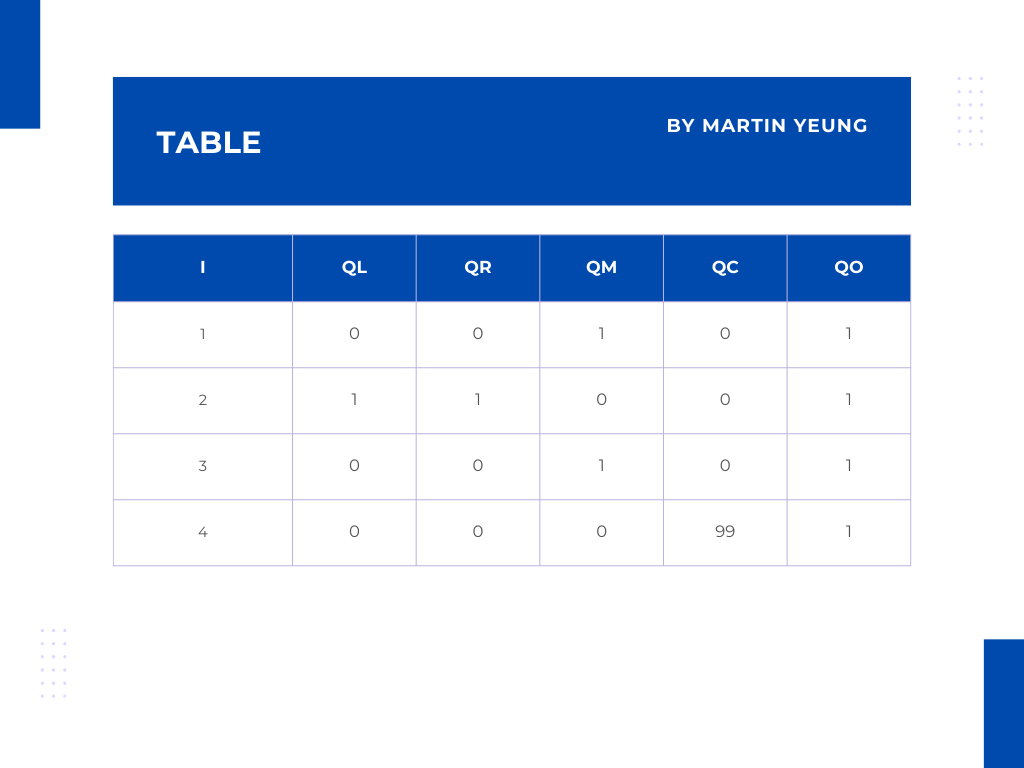

大家可以先仔細理解一下當中的原理，下一篇會深入講解相關的公式及相關原理。