在「統計概念」中，將介紹利用 Python 中的各式分配函數，介紹基礎統計觀念。其中包含：設定不同的參數來呈現分配函數的特性，觀察該分配函數是否為 location-family 或 scale-family；另外，以抽樣方式，設置不同的樣本數，觀察樣本數對分配的影響；並設置一些函數轉換，以實際的程式結果驗證理論；最後，以亂數方式繪製直方圖，與 CDF、ECDF、PDF 與 PMF 圖等相互比較。

分配函數

機率分配的參數數值影響其圖形的長相。機率分配函數分為連續型(Probability Density Function，PDF)與離散型(Probability Mass Function，PMF)，以下分別介紹兩種分配函數，還有參數對分配函數的影響。另，因為同一分配函數有不同的表示方式，造成設定參數後的函數與我們想像的不一致，所以在使用 PDF 或 PMF 之前，建議先上網查看程式表現 PDF 或 PMF 使用哪種型態的表示法。

連續型分配 PDF

若有一隨機變數 X 的樣本空間為不可數，則稱該隨機變數 X 為連續型分配（Continuous Probability Distribution）。-- Statistical Inference，George Casella and Roger L. Berger，98頁。

以下介紹連續型分配，也就是機率密度函數 PDF。

卡方分配

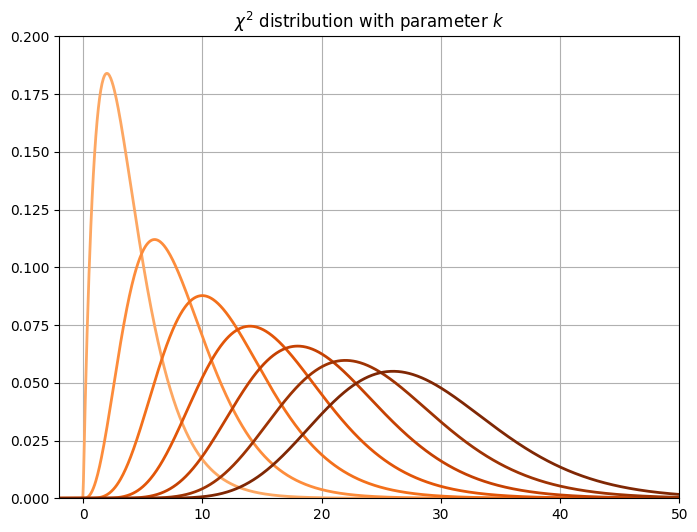
卡方分配在 Python 中的 PDF 程式碼為 chi2.pdf ，其程式所使用的 PDF 如下式。設定不同的參數值 k，可以得到不同的函數取線，如下圖，由左至有的曲線分別為卡方 k = 2, 4, ..., 30。當參數越大線條顏色越深，PDF m 往右側移動。卡方分配 PDF 的最大值（眾數）越大，則其平均值越小。

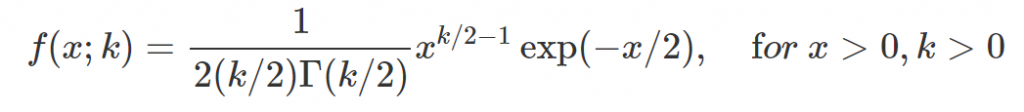
Python 程式碼如下，使用 col = plt.cm.Oranges(np.linspace(0.4, 1, len(df))) 設置線條顏色之變化，並用 for 迴圈一條條畫線，每條線的顏色改用 color=col[i]，讓顏色隨著參數 k 越大而漸深。如若想要觀察每一條線的細微變化，還可以加上 plt.pause(0.5) ，Python 會把一條條把線畫出為獨立的圖，不過此處沒有展示這項技能。

import matplotlib.pyplot as plt
from scipy.stats import chi2
import numpy as np

# chi2

xlim = [-2, 50]
x = np.linspace(xlim[0], xlim[-1], 1000)
df = np.arange(4, 32, 4) # 參數 k 

# color
col = plt.cm.Oranges(np.linspace(0.4, 1, len(df)))

# fill xlim before animation
plt.figure(figsize=[8, 6])
plt.axis([xlim[0], xlim[-1], 0, 0.2])


for i in range(len(df)):
  y = chi2.pdf(x, df[i])
  plt.plot(x, y,lw=2 ,color=col[i])
  # plt.pause # 一條條畫線

plt.grid(True)
plt.title('$\chi^2$ distribution with parameter $k$')
plt.show()

t 分配

t 分配在 Python 的 PDF 程式碼為 t.pdf，其程式所使用的 PDF 如下圖，藉由設定不同之參數值，圖中由上到下的藍色曲線分別為 v = 0.1, 0.2, 0.3, ..., 1 與 3, 6, 9,... , 30 的 t 的購買者，

Beta 分配