註：本文同步更新在Notion!（數學公式會比較好閱讀）

卷積神經網路（Convolutional Neural Networks, CNN）

用於處理具有格狀拓撲結構的數據（例如圖像）的深度神經網路架構。透過卷積層、池化層和全連接層的堆疊，它能夠自動學習圖片中的局部特徵，並進行分類或回歸任務。

• 卷積層Convolution Layer：負責學習局部特徵
• 池化層 Pooling Layer：負責壓縮特徵圖，減少計算量
• 全連接層Fully Connected Layer：負責將提取的特徵轉換成最終的輸出

CNN 的基本結構

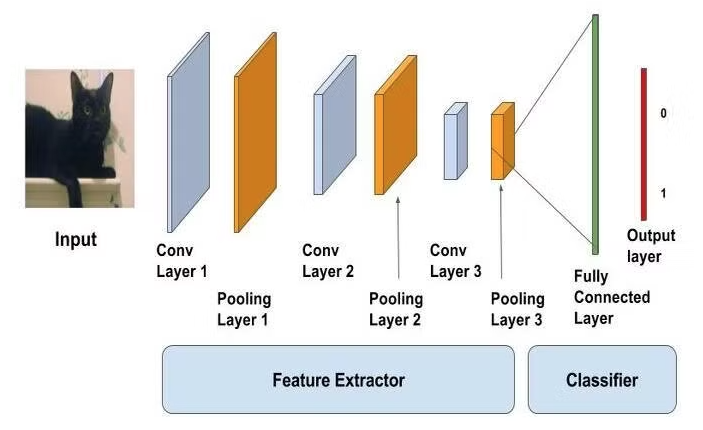
1. 輸入層（Input Layer）

   CNN 的輸入通常是多維數據，如 RGB 圖片可以表示為一個三維張量（tensor），其尺寸為W×H×D，其中W和H表示圖像的寬和高，D表示顏色通道數（例如，RGB 圖片的 D=3。

2. 卷積層（Convolutional Layer）

   卷積層是 CNN 的核心構件。它通過**卷積核（Filter）**對輸入數據進行卷積操作，從中提取局部特徵。數學上，卷積操作可以表示為一個滑動窗口操作，具體公式為：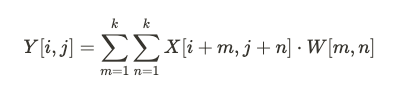
   
   其中 X 是輸入數據，W 是卷積核，Y 是輸出的特徵圖。卷積操作提取了局部區域的信息，因此 CNN 對位置的變化具有較強的強健性。

3. 激勵函數（Activation Function）

   每個卷積層之後通常會接一個非線性激活函數，常見的激活函數是 ReLU（Rectified Linear Unit）：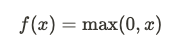
   
   ReLU 函數的作用是引入非線性，允許神經網路學習複雜的模式。

4. 池化層（Pooling Layer）

   池化層的作用是對特徵圖進行下采樣，減少網路的計算量和參數量，並防止過適化。常見的池化方式是最大池化（Max Pooling），其公式為：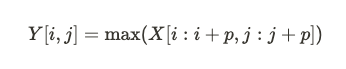
   
   其中 $p$ 是池化的大小，這樣可以保留局部區域內最重要的特徵，同時縮小特徵圖的尺寸。

5. 全連接層（Fully Connected Layer）

   在經過多層卷積和池化後，網路會在最終階段使用一個或多個全連接層。全連接層將輸入的所有特徵結合在一起，並通過Softmax 函數或其他激活函數進行分類或預測。Softmax 函數的公式為：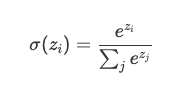
   
   該函數會將輸出的實數值轉換成一個概率分佈，用於多分類問題。

CNN 中的數學基礎

1. 卷積運算（Convolution Operation）

   卷積層是 CNN 中的基礎，數學上卷積是一種特定的矩陣乘積運算。給定輸入數據 X 和卷積核 W，其卷積的結果是：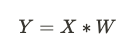
   
   卷積運算具有以下特性：

   • 參數共享：在同一層的所有輸入中使用相同的卷積核，減少了參數量，並增強了模型的泛化能力
   • 接受域(receptive field) ：卷積核僅與輸入數據的局部區域進行運算，這使得 CNN 能夠提取局部特徵

2. 池化運算（Pooling Operation）

   池化層的數學運算與卷積類似，通常採用最大值池化或平均池化。池化運算可以縮小數據的尺寸，並減少模型過擬合的風險。

3. 梯度下降與反向傳播（Backpropagation）

   CNN 的訓練過程與其他神經網路相同，通過**反向傳播算法（Backpropagation）和梯度下降（Gradient Descent）**來優化權重。卷積層的反向傳播需要計算卷積核的梯度，這是通過鏈式法則實現的。

CNN 的應用

CNN 最初是為圖像處理任務設計的，但隨著研究的深入，它被廣泛應用於多種領域，包括：

• 圖像分類：CNN 可以通過學習圖片的局部特徵進行圖像分類
• 物體檢測：R-CNN 等變體在物體檢測任務中表現優異
• 語音識別：CNN 被用來從語音波形中提取特徵，進行語音識別任務
• 自然語言處理：雖然 RNN 和 Transformer 是 NLP 的主要架構，但 CNN 也可用於文本分類和序列處理