註：本文同步更新在Notion!（數學公式會比較好閱讀）

自回歸模型（Autoregressive Model，AR模型） 是一種統計模型，它假設時間序列數據的當前值是其過去值的線性組合。這種模型特別適合處理時間序列數據中的自相關特性，能夠用數學公式描述隨時間變化的動態模式。

1. 數學表示

自回歸模型的基本數學形式為：

2. 自回歸過程中的特徵

自回歸模型基於一個假設，即過去的數據點中蘊含了預測未來的訊息。這種模型能夠有效捕捉數據的趨勢、季節性及其他內在結構。模型的階數 p 通常是根據數據的性質及其自相關特性來選定的。

自相關函數 (ACF) 與偏自相關函數 (PACF)

在建模過程中，自相關函數和偏自相關函數能幫助我們選擇合適的階數 p。ACF 描述了一個時間序列中的值與其不同延遲的值之間的相關性，而 PACF 則測量的是一個點與其直接前一點的相關性，去除了中間點的影響。

3. AR模型與隨機過程

自回歸模型是一種線性模型，假設了時間序列是一個平穩過程。這意味著該過程的均值、方差等統計特性隨時間保持不變。如果時間序列表現出趨勢或季節性變化，我們可以通過差分或其他轉換來使其變得平穩。

應用實例：
假設我們有一組股價的時間序列數據，並希望預測未來的股價。可以使用AR模型來捕捉股價隨時間的自相關特徵，根據過去的價格變化來預測未來的走勢。

5. 數學推導與參數估計

對於AR模型，我們通常使用最小二乘法 (Ordinary Least Squares, OLS) 來估計模型參數 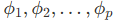。給定時間序列數據 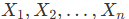，我們能夠利用這些數據最小化預測值與實際值之間的誤差平方和，從而求出最佳參數。

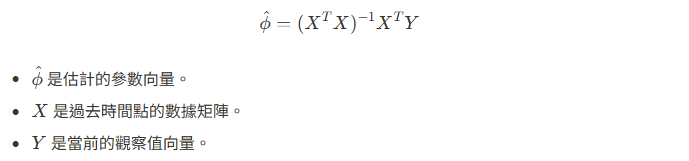
自回歸模型提供了一種數學上簡單但強大的方法來建模時間序列數據。通過捕捉數據中的自相關結構，AR模型能夠生成精確的預測，特別是在短期預測中表現出色。