哈囉，各位之前看了三角函數應該很好睡吧？如果有失眠的問題也可以拿出三角函數來看看，可能對睡眠有所幫助喔！

那今天的內容應該會簡短一些，因為我實在想不到反三角函數可以應用在哪裡...

所以我就會簡單帶過這些函式如何使用以及他的意義跟需要注意的細節，那就讓我們開始吧！

開始前開開嗓，大聲唸出咒語Math.asin()：

「寐偲，阿賽！！！」

數學課

今天要介紹的「反三角函數」其實就是他們各個所對應的三角函數的反函數

反函數？

直接上個圖吧！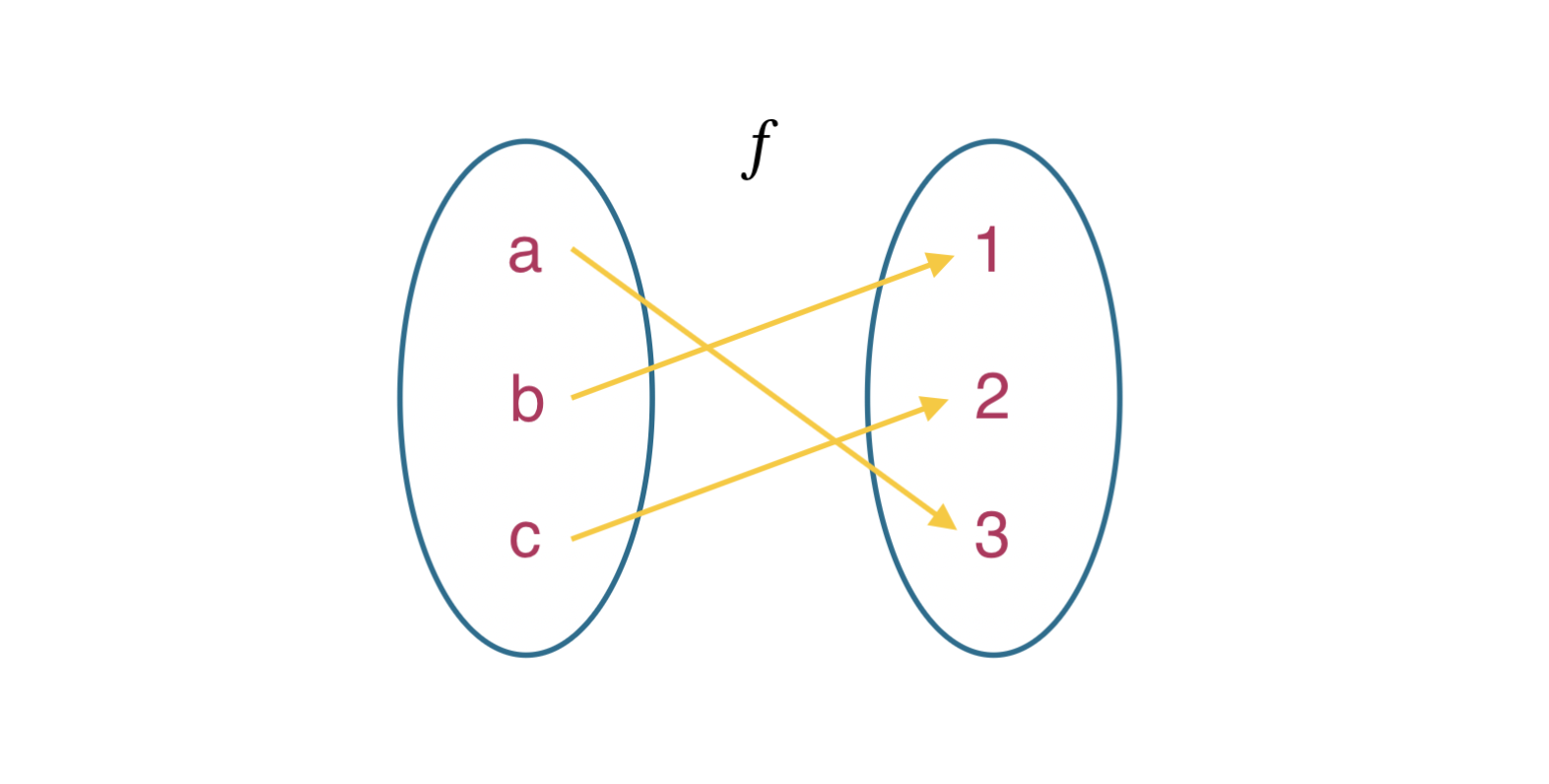

這是一個函數 𝑓 ，當我代入 a 會得到 3，每個代入值會得到一個回傳值：

𝑓(a) = 3
𝑓(b) = 1
𝑓(c) = 2

那 𝑓 的反函式就會是𝑓^-1^：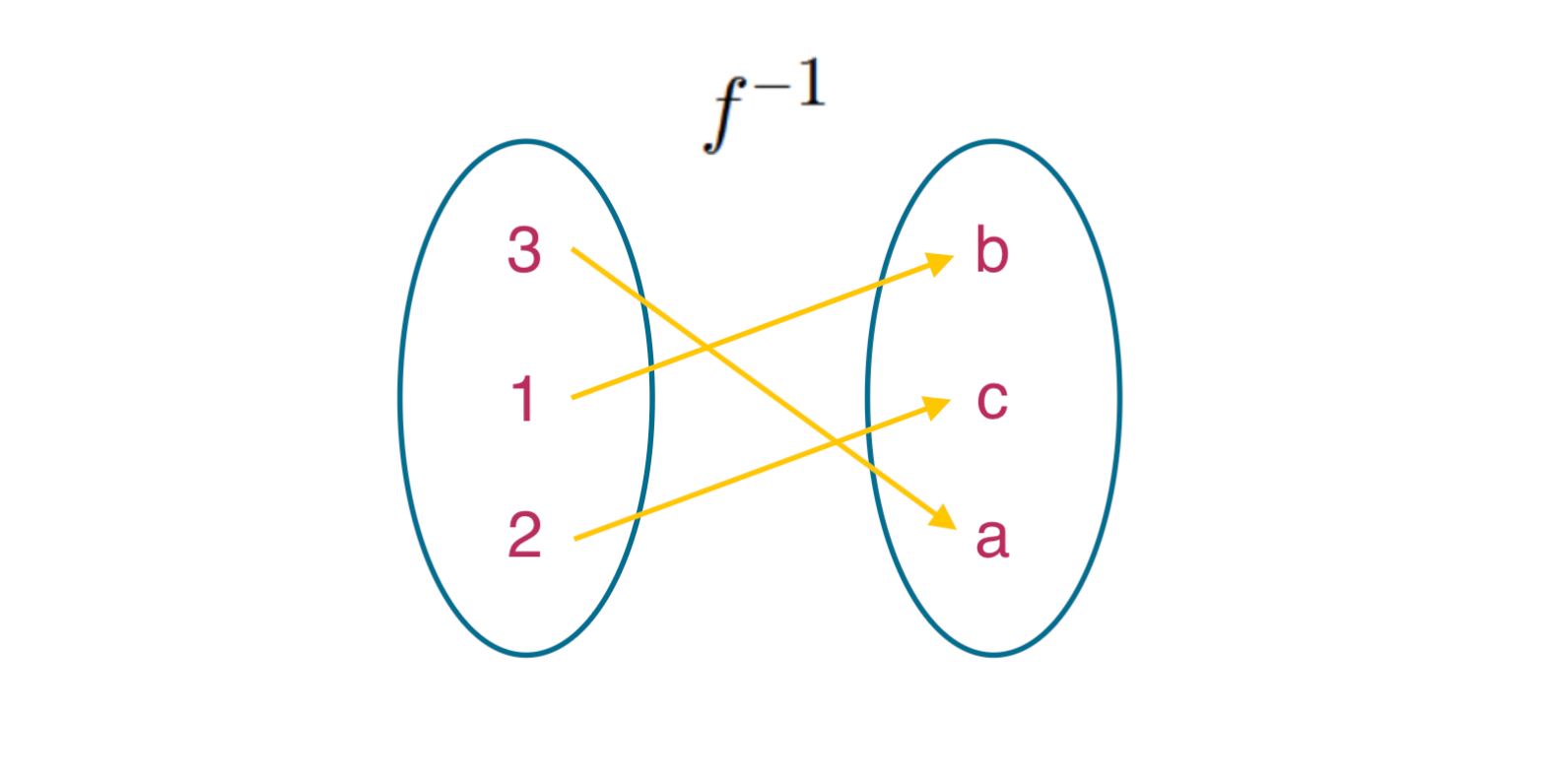

𝑓(3) = a
𝑓(2) = c
𝑓(1) = b

變成輸入之前的結果得到之前的代入～如果這樣還不懂我們試試看帶入日常生活的例子：
假設今天有一個製作洋芋片的機器，我們將馬鈴薯丟進機器裡面他就會產出洋芋片，這時候洋芋片機就是我們的函數，而馬鈴薯就是我們的帶入值，出來的洋芋片就是我們的回傳結果。
洋芋片機函數：

洋芋片機反函數：

太好了！到這邊大家一定都完全理解反函數了！

arcsin

理解完反函數後回到反三角函數，今天要介紹的反正弦函數arcsin就是正弦函數的反函數～

「理解不能。」

OKOK，直接介紹幾個例子：
我們前幾天的章節有介紹過sin函數了，在這，一樣找好觀察的點！

• sin90°(sinπ/2) = 1
• sin270°(sin3π/2) = -1

根據前面反函數的定義，arcsin是sin的反函數

所以將1跟-1代入arcsin應該會得到π/2跟3π/2吧！

嗯...感覺上沒錯，但差了一點點細節，arcsin回傳的範圍會介於-π/2～π/2（含）之間！

所以我們覺得應該是3π/2，實際上他會轉化為最簡同角（範圍落在-π/2～π/2），所以arcsin(-1)的值就會變成-π/2。

理解以後就進入熟悉的環節～來欣賞一下y = arcsinx的圖形吧！

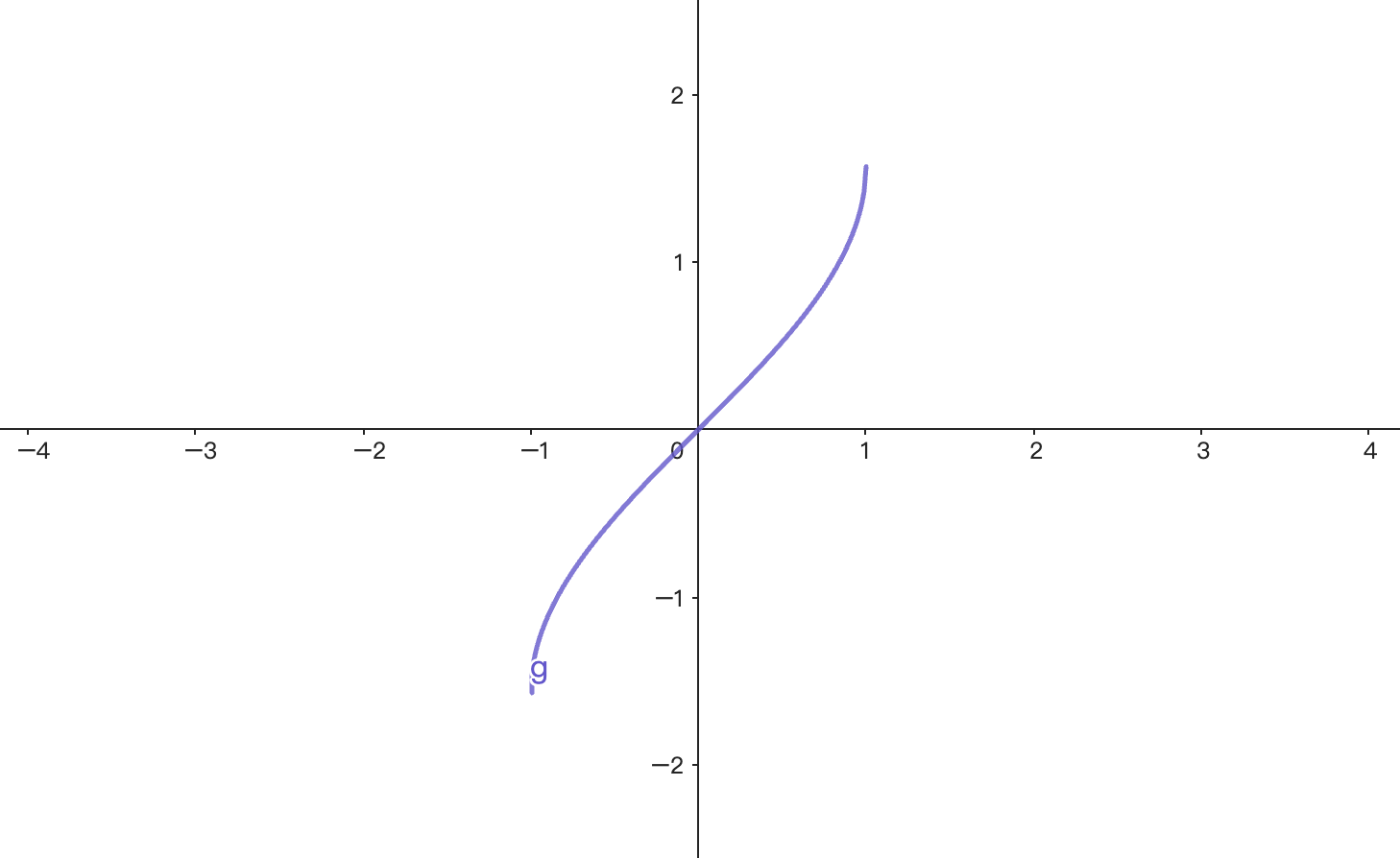
除了美，沒有別的了。

不過這邊有個值得注意的是arcsin函數是一個奇函數！也許這個特性能讓他發揮一些功能喔，留給大家去想想吧！

不知道奇函數可以去搜尋了解一下～

Math.asin()

代表著反正弦函數，通常會用arcsin或是 sin^-1^ 表示。

所以Math.asin()會是Math.sin()的反函數，給一個sin值回傳一個對應的角度值。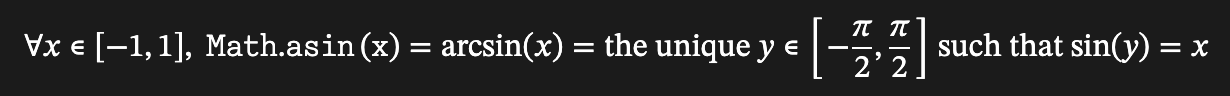

--MDN

語法

Math.asin(x)

參數

傳入一個數字介於-1到1之間（含），這個數字會是一個sin值。

回傳值

他會回傳x的 sin^-1^ 值，回傳值介於-π/2到π/2（含），如果傳入的x小於-1或大於1，回傳NaN。

規範

現在看得非常快了呢！跟前面介紹過的諸多函式大同小異。

直接來使用看看吧！

console.log(Math.asin(0) * 180 / Math.PI); //0
console.log(Math.asin(1) * 180 / Math.PI); //90
console.log(Math.asin(-0) * 180 / Math.PI); //-0
console.log(Math.asin(-1) * 180 / Math.PI); //-90
console.log(Math.asin(Math.sqrt(2) / 2) * 180 / Math.PI); //45.00000000000001
console.log(Math.asin(Math.sqrt(3) / 2) * 180 / Math.PI); //59.99999999999999

一樣我們將數字轉換成角度比較好觀察。（因為180° = π，所以我們將數字乘上180再除以 π 就能得到角度！）

測試中想得到45°跟60°但一樣會有誤差！所以使用上要特別注意～

什麼？你說還有arccos跟arctan嗎？我沒聽清楚麻煩你再說一次，雖然我肯定還是聽不清楚，Sorry了，掰掰明天見。

參考資料：
維基百科-函數
維基百科-反函數
MDN-Math.asin()
ECMAScript-Math.asin()