在之前向大家介紹了PLONE的限制約束，當時只是簡單介紹，現在就深入講解複製約束中的置換證明。

置換證明(Permutation Argument)

首先大家可以先看看以下圖表-向量W: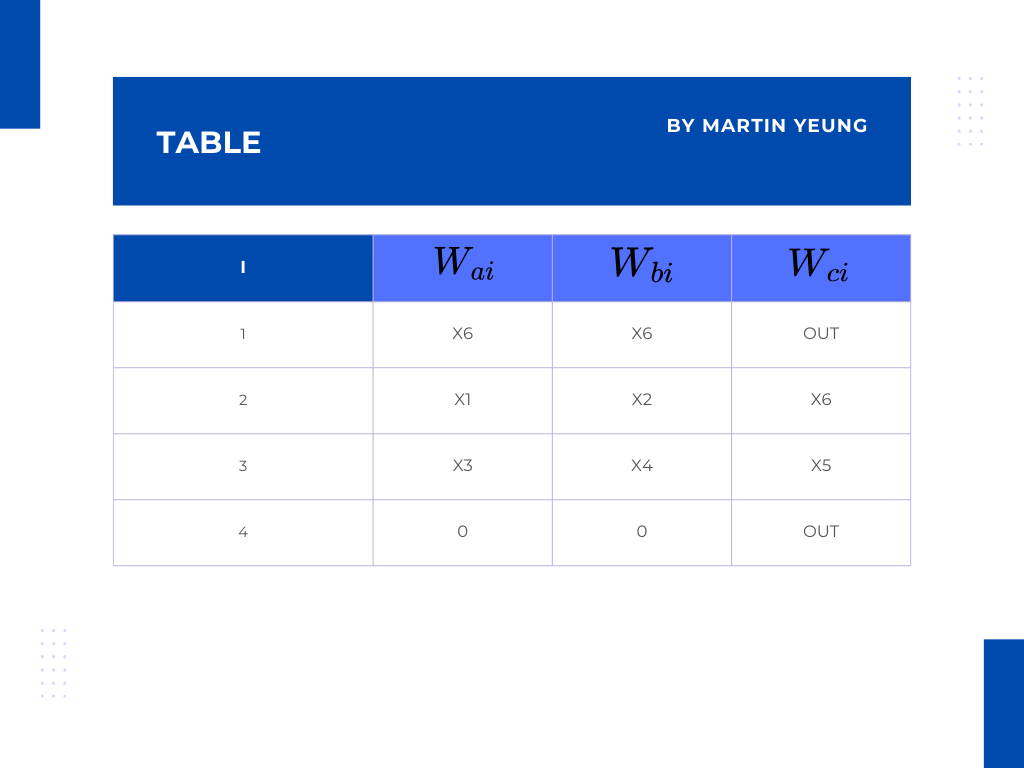

置換證明是一個能實現複製約束的方法。
圖表中就是證明者中將向驗證者發出的證明的限制約束，會看到有4個條件約束。分別是第1, 2, 3, 4行，每行表示一個約束。而圖表中的複製約束關係是 Wa1 = Wc2, Wb1 = Wc3, Wc1 = Wc4，換言之，在Wa1的值是需要被複製到Wc2，在Wb1的值是需要被複製到Wc3及在Wc1的值是需要被複製到Wc4。一旦發現當中的關係出現改變，就表示這個複製約束的條件被破壞了。所以這個複製約束是可以確保某些值是不能在產生證明和驗證證明的過程中被修改。

在置換證明，可以透過剛才的複製約束關係生成另一向量X，而向量X是與向量W相等的，因為可以理解新的向量X中有6個地方的值是進行了互換，就是Wa1的值轉到Wc2, Wb1的值轉到Wc3, Wc1的值轉到Wc4，所以嚴格來說是一個新的向量，不過由於互換的值是相等，所以向量X是等於向量W。

因此，就會有兩個向量具有相等的值，這可以表示兩個向量是存在一個置換關係。要強調一下，置換證明中的置換方式可以有很多種類，涉及到的地方也可以不同的，可以根據需求而設置不同的置換關係。
雖然知道兩個向量是存在一個置換關係，但也需要去證明它，所以在這裡要利用到連乘證明。

連乘證明

要證明連乘關係，就是讓證明者可以利用一組單乘的公式來證明有多個數值的連乘證明，之後再進行多項式編碼來做相關轉換，完成後會發送給驗證者進行驗證。然而，在一個連乘關係會包含多個單乘計算，要做個這個目的就需要加入一個輔助向量來協助將不同的單乘計算連在一起，而這個輔助向量其實就是對上一個單乘計算的結果。

我以下面的例子作說明:
P是多個連乘計算的結果，而q是一個運算結果，而r是一個輔助向量包含對上的的多個q的單乘結果，r的起始值是1。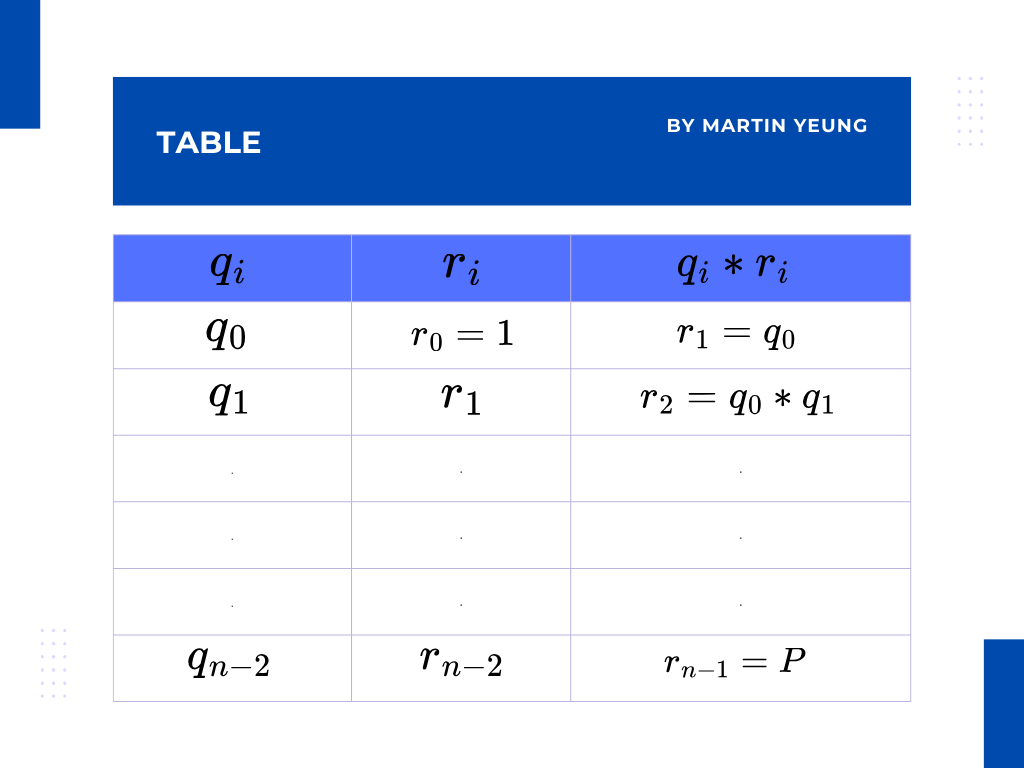

圖中，每一行表示一次單乘，每一行的中間是輔助向量，每一行最後的一個值是表示一次單乘的結果，而這一次單乘的結果會成為下一行的輔助向量。輔助向量可以被視為一個累加器。

累加器(Accumulator)

其實從上面的圖中，可以留意到輔助向量r是不斷累積變大，是一個連乘結果。因此可以視為累加器:

所以會得出下列公式:


因此也會得出下列3個約束:
第1個約束是

第2個約束是

第3個約束是