上一篇講了複製約束中的置換證明，對於當中的計算步驟及原理會在這篇繼續講解。
回顧一下上篇尾段提及到的約束:
第1個約束是

第2個約束是

第3個約束是

可以進一步地將三個約束整合簡化，在連乘表格上再新增一行，使到

如下圖所示: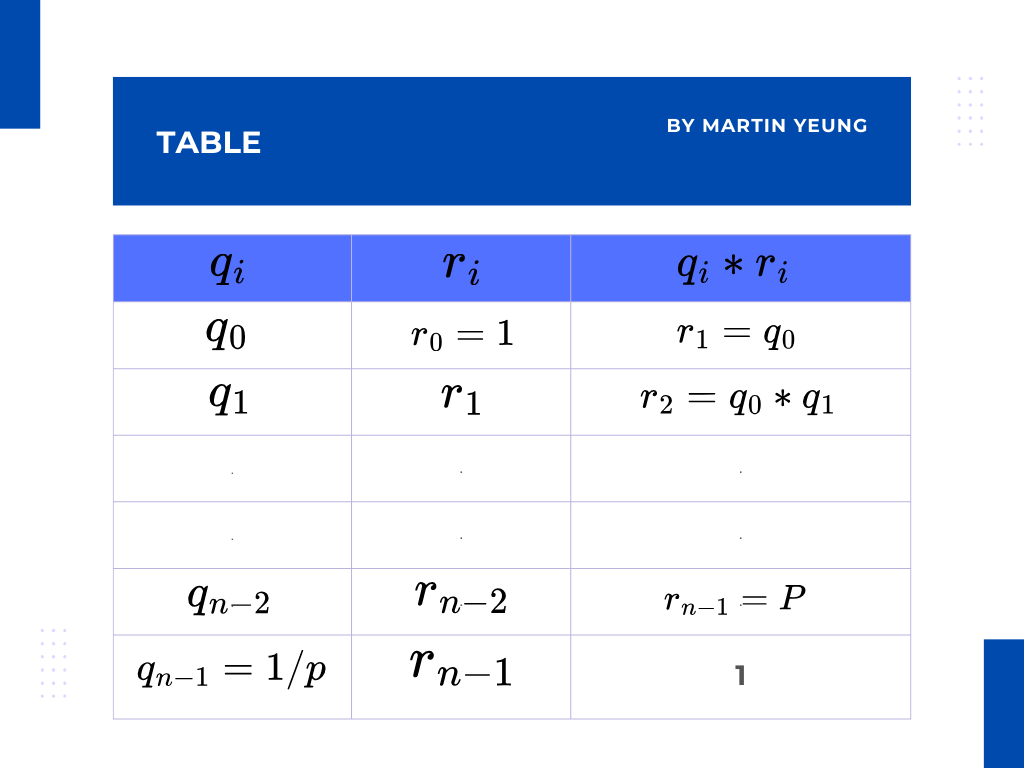

因此可以留意到:

最右的一行就是向量r的循環移位，可以看到第二行的第一列的r是1，而第三行的最後一列也是1。
也可以看到第二行的第一列的r1，而第三行的第一列也是r1。所以形成到一個循環，即兩行所存在的數字的值是一樣，只是相對應數值的位置不同，只要細心觀察就可以一一對應。而且每一行都能夠滿足到乘法關係。
所以可以形成到下面的多項式來表示連乘關係:

在驗證者方面，他可以對下列的多項式進行挑戰:

為什麼會有這個公式呢?
首先左邊的第一個約束

還有左邊的第二個約束

第二個約束可以再轉為:

所以左邊，第一個約束和第二個約束相加在一起會是零

因此:

所以最後會出現以下公式:

有沒有加上a, 也是不會影響到公式結果

α 是一個隨機數，而h(X)是一個商多項式。

大家可以再看看上一篇加以理解，由於當中的原理也是需要時間消化，可以自行多看看。