今天將進入到平面波的繪製，使用的是亥姆霍茲方程 ：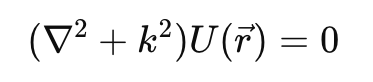

• 這個方程描述的是 波動在多維空間中的傳播，例如三維空間中的聲波或光波。∇2 是拉普拉斯算符，適用於多維空間，表示波動函數在空間中的二階偏導數。U(r) 是波在三維空間中的分佈，k 是波數，決定了波的頻率和波長。

以上來自AI小老師的的講解，我問了一下為何波動函數在空間中的二階偏導數和k平方乘以波在三維空間的分布，結果為0？

AI小老師就幫我推導了一遍，簡單來說：

物理上，這個方程表示波在空間中的分佈是一個特徵值問題。二階空間導數∇2U(r)反映了波函數隨位置的變化速率，與波數 k 相關的項表示波的周期性特徵。當這兩者相互抵消時，波的穩態分佈就是亥姆霍茲方程的解。
這樣的分佈是穩定的，不隨時間變化，且常用於描述光學、聲學等多維波動現象。

其中U(r) ——波在三維空間中的分佈如下：

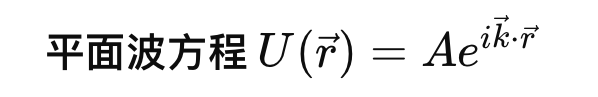
好，公式就到這，開始畫圖囉！

import numpy as np
import matplotlib.pyplot as plt


#定義平面波
def plane_wave(A, k, r, w, t): #A震幅 k波頻 r向量 w角頻率 t時間
    phase = complex(0, np.dot(k, r)-w*t)
    #內積np.dot (dot product, cross product)
    #ωt 是隨著時間變化的相位部分。減去這個項是因為隨著時間的推移。
    #exponential使用負數complex 0為實部，後者為虛部
    return A*np.exp(phase)

#定義波三維方向波速
kx = 0
kz = 2*np.pi*2 #朝z方向行進
k = np.array([kx, kz])

#定義繪圖範圍
D = 5 
N =151 #繪圖細緻度

x_list = [-D/2 +D*i/N for i in range(N)]
z_list = [-D/2 +D*j/N for j in range(N)]
z_2d, x_2d = np.meshgrid(z_list, x_list)
#np.meshgrid產生網格 製作平面

A = 1 #定義震幅
w = 1 #定義角頻率
#定義電場為2維的矩陣
E_field = np.zeros((N, N), dtype = complex) 

#每個迴圈都會帶入x和z的數值，return R數值
for i in range(N):
    for j in range(N):
        r = np.array([x_2d[i,j], z_2d[i,j]])
        E_field[i, j] = plane_wave(A, k, r, w, 0) #定義電場 t給0

#取電場的實部
E_real = E_field.real

#畫圖使用contour (not plot因為plot只能有兩筆資料，三筆資料兩個變數以上就必須用contourf)
plt.contourf(z_2d, x_2d, E_real, cmap = "gray", levels = 99) #cmap為等高線圖色階 levels等高線數 
plt.show()

畫出圖如下：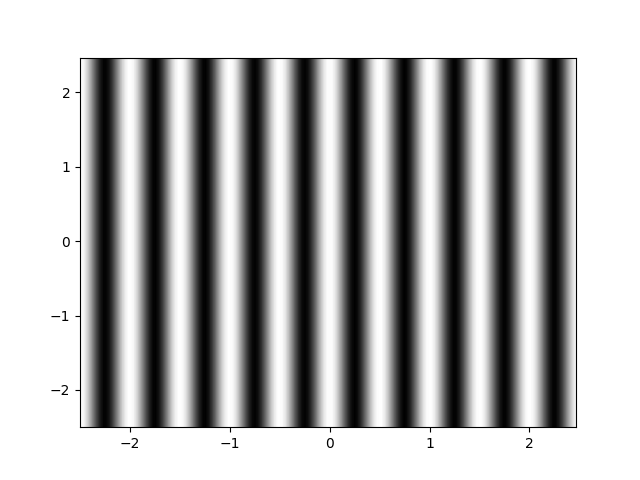

如果x方向也有動量：
kx = 2np.pi2

跑出來的圖中，波的行進方向也會有x軸的向量唷！

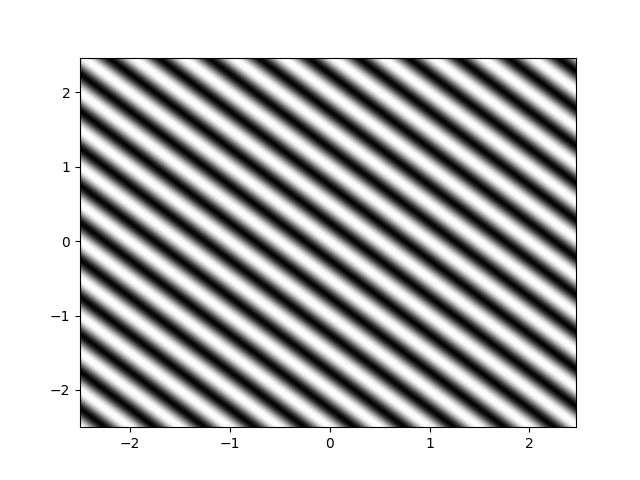
Okie Dokie 今天就到這～再次感謝課堂上助教的python教學，真的是越畫越有趣！
有什麼問題可以問chatGPT，明天就來畫平面波動畫！